

|
|
|
|
Example Algorithm for Steps in Solving Closed-Ended Problems
The elementary, liquid-phase, irreversible reaction
is to be carried out in a flow reactor. Two reactors are available, an 800 dm3 PFR that can only be operated at 300 K and a 200 dm3 CSTR that can be operated at 350 K. The two feed streams to the reactor mix to form a single fee d stream that is equal molar in A and B, with a total volumetric flowrate of 10 dm3/min. Which of the two reactors will give us the highest conversion?
Additional Information: at 300 K, k = 0.07 dm3/mol-min
E = 85000 J/mol-K
CA0B = CB0B = 2 mol/dm 3
vA0 = vB0 = 0.5*v0 = 5 dm3/min
We have two choices, a PFR operated at 300 K and a CSTR operated at 350 K. Which one do we choose?
| Arrhenius Equation: | |
| The higher the temperature, the faster the reaction rate. | |
| Rate Law: |
| Mole Balances: |
Volume of CSTR
Volume of PFR
Independent: V, FA0, T
Dependent: X
Knowns: k0, E, V, n0, CA0B, CB0B
Unknowns: X
In: FA0 = FB0, so QB = 1
Out: FA = FA0(1-X), FB = FA0(1-X), FC = FA0X
Not an issue.
Isothermal, no pressure drop. The CSTR is well mixed. There are no radial variations in the PFR.
There is neither too much redundant information, nor is there too little information given. Therefore, the problem is neither over-specified, nor under-specified.
This problem has a solution procedure in common with Examples 4-2 and 4-4 in the text.
| CSTR | PFR |
![]()
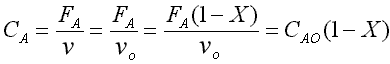
CA = CA0(1-X)
CB = CA0(1-X)
![]()
(eqn 1)
![]()
(eqn 2)
v
A0 = 5 dm3/min
Before mixing
CA0B = 2 mol/dm3
FA0 = CA0B*
vA0
FA0 = (5 dm3/min)(2 mol/dm3) = 10 mol/min
After mixing
v0 =
vA0 +
vB0 =
5 dm3/min + 5 dm3/min = 10 dm3/min
CA0 = 1 mol/dm3
![]()
| at 350 K, | ||
| k = 8.447 dm3/mol-min |
the combined CSTR equation (eqn 1) can be arranged as
![]()
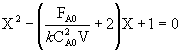

![]()
![]()
![]()
![]()

![]()
Choose the CSTR, because it gives the highest conversion.
X is dimensionless
This is a reasonable conversion.
This the end of the PFR/CSTR example.
A sample registration exam problem
is also available.
![]() Back to Chemical Reaction Engineering Examples
Back to Chemical Reaction Engineering Examples