

(Using values calculated by the density functional method)
The heat of reaction which is usually defined as the difference of the products enthalpy and the reactants enthalpy in this case is not accurate. The enthalpy calculated by the software is solely based on statistical mechanics and does not take into account the ground state energy which is a significant contribution to the total energy of the molecule. But all is not lost, a function of the software is to calculate the ground state energy using quantum mechanics. Therefore we can simply take the sum of the enthalpy and the ground state energy to equal the overall energy of the molecule or total enthalpy, and calculate the heat of reaction by taking the difference between the products and reactants overall energies.
= 16.794 kcal/mol
From this calculation we can see that the reaction is endothermic and needs energy to proceed.
The change in entropy can be simply calculated by taking the difference of product and reactant entropies.
= 0.148 cal/mol K
The Gibbs free energy is normally calculated like so:Since we have already established that the enthalpy is incorrect the above equation can not be used. Therefore, we shall substitute the equation for the heat of reaction into the Gibbs free energy change equation.
= 16.794 kcal/mol
To calculate the equilibrium constant:
= 6.288E-13
This value of the equilibrium constant shows, as expected, that at equilibrium there is a very small amount of CNH in respect to HCN.
The activation energy can be calculated by taking the difference of the transition state enthalpy and the reactant enthalpy. With the enthalpy being defined as the sum of the ground state energy and the statistical mechanically calculated enthalpy.
and
= 46.782 kcal/mol
The preexponential factor can be calculated using some collision theory calculations. Let's just walk through the derivation of the preexponential factor step by step. The first mathematical relationship we will state must be taken as a given since the derivation of the relation is beyond the scope of this explanation. The relation between the rate constant (k) and a pseudo transition state equilibrium constant:(1)
where:(2)
This is very much like the over all equilibrium constant but deals with the transition state instead of the overall reaction. The relation between the transition state equilibrium constant and the Gibbs free energy change of the transition state is:(3)
The Gibbs free energy can be written as:(4)
and substituted into the transition state equilibrium constant relation.(5)
where:
= 4.289 cal/mol KandFinally substitute equation (5) into (1) and(6)
Examining equation (6) we see that it resembles the Arrhenius rate equation.We can see that the first and second terms are equal to the preexponential factor and after defining the activation energy as:we find that the last term is identical to the last term in the Arrhenius rate equation. Therefore, the preexponential is calculated by:
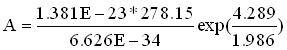
= 5.386E13