First some cool movies!

Here is an animated form of the HCN <=> CNH isomerization:

Here is an animated form of the imaginary frequency of the transition state:

Parameter calculations

We can use the Sum of electronic and thermal Enthalpy of the reactant and products to calculate the overall heat of reaction. Gaussian quotes the energies in hartrees which equal 627.51 kcal/mol. For convienience we will convert all values from hartrees to kcals/mole.

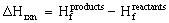
, an endothermic reaction

Change in Entropy of Reaction

The change in entropy can be simply calculated by taking the difference of product and reactant entropies.

Reaction Gibbs Free Energy Change

The Gibbs free energy is calculated:

To calculate the equilibrium constant:

=

This value of the equilibrium constant shows, as expected, that at equilibrium there is a very small amount of CNH with respect to HCN.

The activation energy can be calculated by taking the difference of the transition state enthalpy and the reactant enthalpy.

= -58218.219-(-58266.680) = 48.461 kcal/mol

The preexponential factor can be calculated using some transition state theory calculations. Let's just walk through the derivation of the preexponential factor step by step. The first mathematical relationship we will state must be taken as a given since the derivation of the relation is beyond the scope of this explanation.

The relation between the rate constant (k) and a pseudo transition state equilibrium constant:

(1)

where:

(2)

This is very much like the over all equilibrium constant but deals with the transition state instead of the overall reaction. The relation between the transition state equilibrium constant and the Gibbs free energy change of the transition state is:

(3)

The Gibbs free energy can be written as:

and substituted into the transition state equilibrium constant relation.

(5)

where:

Finally substitute equation (5) into (1) and

Examining equation (6) we see that it resembles the Arrhenius rate equation.

We can see that the first and second terms are equal to the preexponential factor and after defining the activation energy as:

we find that the last term is identical to the last term in the Arrhenius rate equation. Therefore, the preexponential is calculated by:

With these quantities we could readily go ahead with a non-isothermal reactor design.

Lets move on and review what we have learned.