Mass Balance Derivation

The equation below formulates the general mass balance that takes into consideration radial variations and unsteady-state condition in a tubular reactor. This derivation is based on equation (8-86) in section 8-9 without the steady-state assumption.

                                   

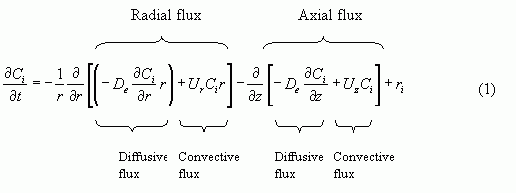
Where C_i is the concentration of species i, (mole/m³)

       D_e the effective diffusivity, (m²/s)

       U_r and U_z the superficial velocity in the radial and axial directions respectively, (m/s)

        and r_i the reaction rate of species i (r_i = v _i*(-r_A)), (mole/m³/s)

In Eqn (1), the term on the left hand side represents accumulation. The first two terms on the right hand side represents the difference in flux over a volume element. The total flux consists of two parts; Flux by diffusion and convection both in a radial direction and axially.

If the flux of one species out of the specific volume element is less than the flux going in to the same element that implies that this species is accumulating or disappearing through reaction. Therefore the sum of the accumulation and the net flux equals the reaction rate. Since the reaction is studied time dependently in this case the accumulation term must be included.

Assumptions

The convective flux in the radial direction is smaller than the diffusive flux and can therefore be neglected, i.e. U_r is approximately 0. Therefore the radial flux will only consist of the diffusive term. 

                                                  (2)

Furthermore, we assume that U_z is constant and equal to the inlet velocity throughout the reactor.

                                                        (3)

Expanding the derivative of the radial diffusivity yields the final form of the general mass balance being used in this exercise:

                                                            (4)

Since there are three spices in the reactor (A, B, and C), one mass balance for each spices is needed for unsteady-state modeling.

For A:                                           (5)

For B:                                           (6)

For C:                                      (7)

Where the reaction rates are connected to each other as , .

These equations represent the simplified general forms of Eqn (1) that has been used by COMSOL Multiphysics to solve the unsteady-state plug flow reactor problem stated.