We have seen in Figure 10-34 that etching (i.e., the dissolution or physical or chemical removal of material) is also an important step in the fabrication process. Etching takes on a priority role in microelectronics manufacturing because of the need to create well-defined structures from an essentially homogeneous material. In integrated circuits, etching is necessary to remove unwanted material that could provide alternative pathways for electrons and thus hinder operation of the circuit. Etching is also of vital importance in the fabrication of micromechanical and optoelectronic devices. By selectively etching semiconductor surfaces it is possible to fabricate motors and valves, ultrasmall diaphragms that can sense differences in pressure, or cantilever beams that can sense acceleration. In each of these applications proper etching is crucial to remove material that would either short out a circuit or hinder movement of the micromechanical device.

Dry etching involves gas-phase reactions (usually in plasmas) which form highly reactive species that impinge on the surface to react with the surface, to erode the surface, or both. In the fabrication of optoelectronic devices, dry etching is used almost exclusively. Indium phosphide is a material that is used in the fabrication of optoelectronic devices, but it is an extremely difficult material to etch.

One technique that has been used to etch InP successfully is reactive ion etching (RIE). RIE involves the formation of highly reactive species, usually in a plasma, which impinge on the surface to react with and to erode the surface. To illustrate the principles of RIE, we will study the etching of InP in an argon plasma. Typical reactions that occur in the gas-phase plasma (which generates high-energy electrons) are

A schematic of the plasma is shown in Figure CD10-5.

Figure CD10-5
Schematic of ion bombardment taking place on the wafer
[Courtesy of Semiconductor Int., 15 (6) 72 (1992)]

Typical operating conditions are shown in Table CD10-3.

Figure CD10-6
Plasma interactions with a surface

We now look specifically at the reactive ion etching of InP. The removal of InP from the surface can occur by two mechanisms. In the first mechanism, InP is removed as a result of bombardment from a high-energy argon ion which knocks InP off the surface. This type of etch, called sputtering or sputter etching, is simply erosion of the surface; no chemical reactions are involved (Figure CD10-7). In the second mechanism a reaction takes place between InP and

Figure CD10-7
Etching by sputtering

chlorine to form InCl ₃ . The more volatile InCl ₃ is removed from the surface either by argon or by vaporization ion bombardment (Figure CD10-8). Because a reaction takes place before removal of the material it is called reactive ion etching. We shall now consider the RIE of InP in more detail.

The chlorine atoms that are generated react with the surface according to the following sequence ⁴ :

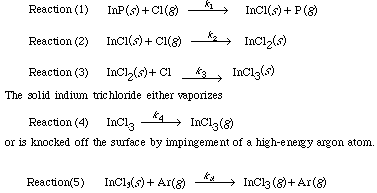
This last step is a sputtering reaction.

Figure CD10-8
RIE etching

We now proceed to prepare a law for the rate of etching in terms of the concentrations of argon and chlorine. We assume that each step in the etching process is elementary. The net rate of removal of indium from the surface is the sum of that removed by both Reactions (4) and (5):

where (Ar) is the concentration of argon above the surface andis the fraction of the surface covered by InCl ₃.

Net Rate of Formation of Reactive Intermediates

The chemical species InCl and InCl ₂ are unstable reactive intermediates. Because the etching takes place at steady state, there is no net rate of formation of these species. That is, they react virtually as fast as they are formed. For Reactions (1) and (2), which are elementary, the net rate is

Solving for the fraction of the surface covered by InCl gives

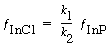
Similarly, the net rate of formation of InCl ₂ is zero, and Reactions (2) and (3) give

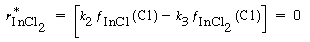
Solving for the fraction of surface covered by InCl ₂ yields

Finally, the net rate of formation of InCl ₃ is also zero at steady state. Reactions (3), (4), and (5) give

Solving for the fractional coverage of InCl ₃ , we obtain

Next we carry out a fractional surface-area balance:

Substituting for InCl, InCl ₂ , and InCl ₃ yields

Combining Equations (CD10-21) and (CD10-27), we obtain

Substituting for°_InP in Equation (CD10-30), and multiplying numerator and denominator byand dividing by k ₁ , the etch rate law for RIE of indium phosphide becomes

A nonlinear least squares analysis (discussed in Chapter 5) gives k _t = 400, k _4/A = 0.001, and k _t/A = 0.095. Figure CD10-9 shows the experimental etch rate as a function of the predicted etch rate shown on the right-hand side of Equation (CD10-31). A photo-correlation spectroscopy analysis of the surface being etched reveals that the surface is primarily InP and InCl ₃ , with virtually no InCl and InCl ₂ :

Consequently, for all practical purposes the etch rate can be written as

Wet etching is used primarily in micromachining, where acids are used to dissolve the solid substrate to form intricate channels and slopes, but it has also been used in the fabrication of computer chips. Figure CD10-10 shows a schematic of the etching process of material A. When a chemical etch is to be carried out, the portion of the material that is not to be etched is covered by a polymer coating called a photoresist, which prevents it from contacting the acid.

Next, the area of material A that is unprotected by the photoresist is etched away until the acid reaches material B and completes the channel formation. Finally, the photoresist is removed by immersing the chip in the appropriate solvent. In many instances we want to stop the etching process as soon as we reach the A/B interface. To achieve this etch stop as precisely as possible, we need to know the rate of etching. Consequently, in this section we

Figure CD10-9
Wet etching

focus on the rate of etching (i.e., rate of dissolution of solid materials) to develop mechanisms and rate laws.

As an example of etching, consider the dissolution of a silicate in hydrofluoric acid. First consider the dissolution in which no liquid-phase catalysts are used. The acid, A (e.g., HF), adsorbs reversibly on a site S on the substrate surface (Figure CD10-11). Symbolically, we have

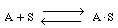
Figure CD10-11
Adsorption of HF

The adsorbed acid breaks the Si-O bonds on the substrate surface, thereby dissolving it and generating products that go into the liquid phase. These products (Si, O) undergo a series of rapid homogeneous reactions which produce SiF₄ and H ₂ O. When these products go into solution, they uncover the next molecular layer of substrate to be dissolved, as shown in Figure CD10-12.

Figure CD10-12
Surface reaction

We can write the surface reaction symbolically as

The symbol S in this reaction represents the new substrate surface that has been exposed to acid once the layer above it has been removed. As with catalytic reactions, the surface reaction is most often rate-limiting, in which case we have

where f_AS is the fraction of the surface that has A adsorbed. For the adsorption step, the rate of adsorption

where a _A is the activity of the acid in solution. For ideal solutions we can replace a by the concentration C _A . Because surface reaction is rate-limiting,

The fractional surface area balance is

Substituting for f_AS and solving for f _v gives us

Combing Equations (CD10-33), (CD10-35), and (CD10-37), we obtain the etch rate as

For activity coefficients of approximately unity, the rate expression becomes

Figure CD10-13 shows the dissolution of the aluminosilicate montmorillonite as a function of HF concentration ⁵ . The corresponding rate law is

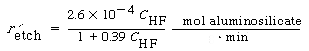
Figure CD10-13
Rate of etching as a function of HF concentration

Dissolution catalysis is the process in which a species that has no dissolving capacity is added to a system to accelerate the rate of dissolution. To illustrate this process, we shall consider the aluminosilicate system just discussed, except that this time we will add a dissolving catalyst B (e.g., H+ ). In this system, B can only adsorb on specific sites on the surface, S´ . These sites are different from those sites upon which A can adsorb.

The adsorption process shown schematically in Figure CD10-14 can be written symbolically as

Next we have the adsorption of A (HF) on S-type sites (Figure CD10-15):

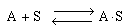
Figure CD10-14
Adsorption of H+ (i.e. Species B)

Figure CD10-15
Adsorption of HF (i.e. Species A)

Finally, the surface reaction takes place in which silicon and oxygen are removed from the surface exposing the next layer of silicon and oxygen (Figure CD10-16). The surface reaction is

and the corresponding rate law for the catalytic dissolution is

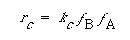
Figure CD10-16
Surface reaction

Because the adsorption of B is not rate-limiting,

Solving for the fraction of S´ sites occupied by the catalyst B gives us

from a site balance of only those sites on which B can adsorb:

Combining Equations (CD10-39), (CD10-44), (CD10-45), and (CD10-46), we obtain

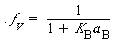
The total rate of dissolution is the sum of the uncatalyzed rate [Equation (CD10-39)] and the catalyzed rate [Equation (CD10-48)]:

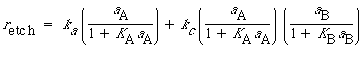
The degree of catalysis, D _AC , is defined as the catalyzed rate minus the uncatalyzed rate, divided by the uncatalyzed rate:

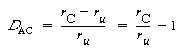
Substituting for the uncatalyzed rate equation (CD10-39) and the catalyzed rate equation (CD10-48) gives

Figure CD10-17 shows a plot of the degree of catalysis as a function of hydrogen ion activity for the dissolution of the aluminosilicate kaolinite. Taking the reciprocal of Equation (CD10-52), we obtain

Figure CD10-17
Acceleration of kaolinite dissolution rates by HCI

Figure CD10-18 shows the etch rate as a function of catalyst activity ⁶ . We see that a plot of 1/D _AC versus 1/a _B should be a straight line

Figure CD10-18
Linearization of model for the catalyzed dissolution of kaolinite