ADIABATIC LAMINAR FLOW WITH NO RADIAL MASS TRANSPORT AND NO AXIAL DIFFUSION

Mass and energy balance

So far, we have assumed fully developed turbulent flow, i.e. plug flow. For the adiabatic case, this assumption allowed you to neglect all radial effects, reducing the problem to a one-dimensional problem. Let us now make a first attempt to use laminar flow instead of turbulent flow. To make it a bit easier, let us assume that the diffusivity is zero, i.e, D_i = 0 and also, let us remove the cooling jacket.

For laminar flow, the axial velocity profile is:

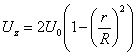                     (14)

U_z is the laminar velocity,

U₀ is the average velocity,

R is the actual radius of the tubular reactor,

and r is the radial distance from the center of the reactor.

Almost the same equations and boundary conditions are solved for this problem as for the previous problem with turbulent flow and cooling jacket. The only changes are due to the assumption D_i = 0 and to the expression of laminar flow.

                                                                             (15)

               (11)

Remember that U_z in Eqn (15) and (11) is the laminar velocity displayed in Eqn (14) and not the turbulent flow.

Boundary conditions

Even though the problem seems to be reduced to a one-dimensional problem with respect to the mass transfer, this is not true. The reaction rate term is dependent of the temperature and since the temperature varies along the radius, the mass balance has a two-dimensional dependence.

At the center boundary, we again assume symmetry or insulation, meaning that there is no net flux leaving or entering the center boundary in the radial direction. This boundary condition comes from the fact that there are no radial concentration gradients over the volume element in the center of the reactor.

No mass can leave the reactor through the reactor wall though the boundary is insulated. The wall boundary condition will therefore be the same as for the center; there are no radial concentration gradients over the volume element close to the reactor wall.

An adiabatic system does not exchange energy with its surrounding. The wall boundary is insulated and the wall boundary condition is identical to the center boundary condition: there is no net flux of energy. This condition translates, in the same way as before, into that there are no radial temperature gradients over a small volume element close to the reactor wall.             

                         Mass/Mole condition       Energy condition

at z = 0           

   at r = 0            

   at r = R           

We changed the turbulent flow to a laminar flow but radial effects with respect to the mass transport are still neglected. What do you expect the plot to look like compared to the turbulent case without heat exchange effects?