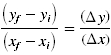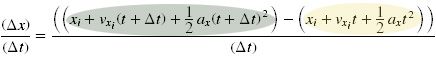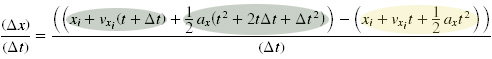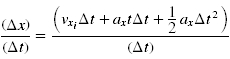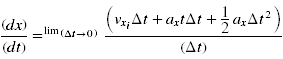Learning Physics 01
Download Physics Equations 01 - Jim.epub - - - Home
I decided to learn Theoretical Physics after finding some video lectures from Stanford University taught by Leonard Susskind. They were fascinating but I could only follow the bare bones of what was being taught. I figured I needed to fill in the holes I had in Mathematics. As I delved deeper into trying to build a firm foundation on which to build I found out that I really did not know very much. I want to understand what this universe was made of and in so doing I would gain a knowledge of how that stuff interacted. At every turn I found more avenues that piqued my interest.
The Mathematics of the 17th, 18th, and 19th Centuries reads like High Adventure exploring new vistas and yes, filled with intrigue. The scope of Set Theory, Geometry, and Algebra are truly mind bending. Concepts and tools developed from those times onward devoured my time. Eventually, I digested enough scraps of information and clarified my goal. I am where I am and this is how I will get to where I will be.
I want to see the Equations of Physics as stuff interacting with stuff. I want to see the Form and Motion. So, I need to know the language. What follows is a fairly narrow track of pronunciation and definitions. I have realized that a definition in a living language does not stand in isolation. It is the inter connectivity of words that create concepts that resolve to comprehension. From time to time there will be a "path not taken" which is a note to myself to stay on the topic at hand. It refers to just grazing the outskirts of a concept that holds promise of worthwhile investigation. I may endeavour to mention such "Paths not Taken" in the final section but it will without a doubt be incomplete.
Is this anything?

Physics is an experimental science. Measured quantities are known in Physics. Physics endeavours to express these quantities in their fundamental form. An experiment detects an interaction between the apparatus and the thing being measured. An experiment gives reproducible results anywhere it is performed in the Universe. These constraints on observations allow the Physics Equation to model the stuff and interactions.
Are Stuff and Interaction two things? I don't know.
Experiments give rise to data which Physics Equations model in a fundamental form. Newton is credited with this Law: "For every action, there is an equal and opposite reaction.". The short rewrite ![]() , F 12 equals negative F 21, fits into the larger schema of Physics. When thinking or speaking Physics Equations it is helpful to pronounce them correctly to facilitate communication. Many branches of Mathematics provide the Relationships of the Observable's in Physics.
, F 12 equals negative F 21, fits into the larger schema of Physics. When thinking or speaking Physics Equations it is helpful to pronounce them correctly to facilitate communication. Many branches of Mathematics provide the Relationships of the Observable's in Physics.
Mathematics is a rich science of diverse content. Discovering what content and depth to comprehend Physics is an intrepid expedition. Encountering Sirens can be anticipated, but recognizing them is another matter. Fortunately, no knowledge is wasted and a dalliance with a Siren is often rewarding. The Observer affects what is being Observed. The needs of Physics might be less than what Mathematics has to offer. A Drunken Walk might be the path to comprehending Physics Equations.
To bypass the Mathematical Drunken Walk go directly to...OK, Physics
Calculus, Algebra, Geometry, Trigonometry: What requisite parts?
A derivative is a specific case for a Limit. A Limit performs an action on a function. A function defines a relationship among variables. A variable is a measured quantity. Functions come in Families. Mathematics defines a function and gives its meaning to those who can read mathematics. Mathematics relates one family member to another. A function and its derivative are members of a family.
I heard Richard Feynman say, "Mathematics is more than a Language. It is Language and Reason." Between each symbol of a function and between each function of a family is a logical structure. You can comprehend Mathematics by understanding the Symbols and the Logic. You need both just for mathematics. Physics Equations need Mathematics to model the Stuff and Interactions. The values of the stuff and interactions are measured or calculated quantities in Physics. You can comprehend Physics by understanding the Symbols and the Logic.
Position, velocity, and acceleration is a Family. Mass, momentum, and force is a Family. Mathematics relates these two families but that is a path not taken at this time. The path of position, velocity, and acceleration illustrates a derivative family of three members in the intersection of the Mathematical and Physical Realms. Let's be blunt, people like, Aristotle (384 BC – 322 BC), Galileo (1564 – 1642), and Newton (1642 – 1727) observed how objects moved, measured the times and distances involved and distilled a statement to describe the relationship. Most of Science illuminates "How stuff is" until you get to the furthest edge where it mingles with insight, imagination, science fiction, philosophy, and theology. So Science sheds a tantalizing glimmer of answers on "the Why-ish questions" at the furthest frontiers. The "How" and "Why-ish" appear to be the range of Science.
OK, hold an object in your hand which is unbreakable and has some weight to it. Now drop it. Note that it took some time to fall some distance. All stuff does this in the same relationship of distance to time. Why-ish did it fall?
The acceleration due to gravity acts on everything, Your hand supports the object at an initial position and you perceive the support as the object's weight. When you remove your hand the acceleration due to gravity acting on the object causes it to move in a specific manner.
How did it fall?
When you remove your hand the acceleration due to gravity acting on the object causes it to move in a specific manner. If you toss the object from your hand the acceleration due to gravity acting on the object remains the same, however any part of the speed of the toss that is parallel to the acceleration due to gravity will effect the time it took for the object to fall. Written as
and is read as the following.
The final position, x sub final, equal the initial position x sub initial, plus the initial velocity, v sub x initial, parallel to the acceleration due to gravity multiplied by the time, plus one-half the acceleration due to gravity, a sub x, multiplied by time squared.
Straddling Mathematics and Physics
A function operates on a variable that results in another variable that is dependent on the function as a definition and the initial variable as its input. The range of the input variable is restricted by what is or can be measured and the logic of the function when it processes that input. The output exists within the domain of the functional operation. The function f of x equals y is written y = f(x). The labels f, x, and y are conceptually arbitrary but there are centuries of tradition that dictate how one talks these things in polite company.
In the foundations of Calculus is the Limit operator. There is a special case of the Limit which is defined as the Derivative operator. I hear the Siren's Song just thinking about the Limit. Physics Equations need the Limit, but the vast scope and awesome power of the Limit makes it difficult to stay my course to a single path when I glimpse the vistas of this Magnificent Realm. I fear and freely admit I will not do justice to the Limit as an Artisan may, nor as a mechanic who crafts their own tools. I resign myself to planting a seed acquired from this Mathematical land.
Physics Equations are Models
The models are specific definitions of positions, motions, and forces. They represent the properties and relationships of stuff and interactions. When a function operates on an input it produces and output. Supplying a different input renders a different output.
In this specific case where x 1 changes to x 2 results in y 1 changing to y 2. The change in y as the result of the change in x is the average rate of change of the function f(x)., y sub 1 equals f of x sub 1 and
, y sub 2 equals f of x sub 2
is the average rate of change of the function between two specific points. Now, let x be any two arbitrary values in the range of f(x) that are very close to each other. Choose the initial and final values of x even closer together than x 1 and x 2 are.
, y 2 minus y 1 over x 2 minus x 1 equals delta y 21 over delta x 21,
, y final minus y initial over x final minus x initial equals delta y over delta x.
This re-write is more general but it remains the average rate of change of the function albeit now between two arbitrary points. Proving that one can select an input value arbitrarily close to another input value that produces a valid output value will also produce a valid output value is "really cool". A mathematician would say simple and elegant, but this to is a path not taken at this time.
It gets Bumpy from Here
Notice that x f - x i = Δx can be written x f = x i + Δx where both x f and x i are still within the range of f(x). Also, y f - y i = Δy can be written y f = y i + Δy where both y f and y i are still within the domain of f(x). In this neighbourhood of x f, x i, and y f, y i, and let x, y, and y = f(x) exist and be continuous. The concepts of "neighbourhood" and "continuous" are a result of "a path not taken". So y = f(x) can also be written as y = f(x + Δx) which also exists and is continuous. The average rate of change of the function can be written as
Replacing the label f() with the function, say this one
, delta y over delta x equals the difference of functions f of x plus delta x minus the function f of x over delta x.
Substituting the Physics Equation P(t) into the average rate of change definition give rise to symbols that can be simplified using Algebra or Trigonometry.
where x f is a label for function of position over a range of time.Since x f is just a Label it can be replaced by P(t) which means the same thing. It is easier for me to see that position is a function of time by writing P(t). Observable Quantities of Time come into the function and Observable Quantities of Length go out of the function, thus x = P(t).x i is the starting position measured in Length
v x i is the starting velocity measured in Length per Time
and a x is the acceleration measured in Length per Time squaredTake note that x i, v x i, and a x are constant values in this expression. Also the subscript x in v x i and a x indicate these vectors are parallel to the x-axis. The "x-axis" is just a straight line from here to over there. The function maps Time onto Length and the symbols are identified.
, the position x equals the function P of time t, equals the initial position x i, plus the initial velocity v x i along the x-axis multiplied by the time, plus one-half the acceleration a x along the x-axis multiplied by time squared.
the first instance of function P takes the argument t plus delta t and the second instance of function P takes the argument t
the second instance of function P looks nice and neat, while the first instance has the t plus delta t terms which will make the whole thing messier before it can become neat and clean
expanding t plus delta t squared results in the manageable middle term
a little bit of multiplication gets rid of most of the parentheses
a little bit of arithmetic gets rid of the rest of the parentheses
rearranging the terms makes it apparent which terms cancel and you are left with a nice and neat equation
Note that the function P(t) relates position to time. This function relates the average rate of change of position to time.
Enter the Limit
The function that defines the instantaneous rate of change at every value of x requires that Δx = 0. Since division by zero is undefined the Limit operator is used to define this derivative as Δx approaches zero. The derivative dy/dx equals the limit as delta x approaches zero for the difference of functions f of x plus delta x minus f of x over delta x
The Derivative Definition can be used with a wide variety of functions and variables. So, for the freely Falling object you have
Divide by Δt before it reaches zero in the Limit Expression
Then let Δt reaches zero to eliminate any term containing Δt
Thus, the Limit operator notation and the delta t terms disappear leaving a calculatable function
A Derivative operating on a function results in a function defining the rate of change of that function. Thus the first derivative of Position is the Velocity and applying the derivative operation to the Velocity results in the Acceleration which can also be called the second derivative of Position.
Position
Velocity
Acceleration
The "derivative of f" has many names: "d dx of f", "d f", "f prime", "dy dx" "y prime", "y dot", and some other name mangling to designate the second, third, fourth derivative, and so on. A sampling of such notation is as follows
The derivative operator sheds light on the deeper structure of a function. The structure is there even when I don't know about it. Say the initial function was constructed from the observation of an apple falling from a tree. Or a thrown stone. Or the flight of a canon ball. Or the path of the Moon around the Earth. Or the orbits of the planets around the Sun. Truth be told, with careful measurement and an understand of what the symbols mean the Family of functions hold together the observations from apple to planets.
Other Families of Observed Phenomena can be mapped into other Equations of Physics which are much more complex than the ones for apples and planets. There are equations that describe heat, sound, electricity, pressure, fluids, and well just about anything you can perceive. They measure many factors interacting with each other. Once you get a hold of one of them the derivative can shed light on unifying principles that, usually after some messy looking mathematics reveals some measure of satisfying understanding. So, its worth the while to appreciate that the derivative operator can be applied to a very wide range of equations.
It is worth repeating, "The derivative dy/dx equals the limit as delta x approaches zero for the difference of functions f of x plus delta x minus f of x over delta x",
because it is the primary concept of Calculus. The f can be any function that defines a Stuff or Interaction in Physics. The x can be any quantity or group of quantities in Physics. The derivative defines how Stuff or Interaction change.
We perceive a Physical World of Stuff and Interaction which we intuitively and often unconsciously grasp. There are a few more mathematical paths to walk in order to speak clearly in the Language of Physics. The derivative however is a very important step. It is very large step and its importance can not be under estimated. If the concept seems simple and you might ask, "How can it be that big of a deal?", then you have grasped the idea.
The idea is simple. Implementing the idea and solving an equation can become very difficult. Without seeing a Physical meaning for the effort required to solve derivatives will dissuades most people from making the attempt. I need to learn Mathematics hand-in-hand with Physics or I, at worst lose interest in both out of shear frustration or at best feel a wow-that's-cool sense that I can't do anything with. Traditional methods of teaching Mathematics more often than not succumb to this downfall. I will indulge in this malady presently, but with the following disclaimers. First: I generated the ensuing graphic before I started writing these notes which you are currently reading. Second: Greek letters happen a lot in Physics and I have a hard time hearing the difference between psi Ψ ψ and phi Φ φ. Third: The derivatives are defined for continuous functions u and v, and the constant "a" by applying the Derivative Operation ![]() then skipping the messy Algebraic steps to resolve a nice and neat equation. Fourth: I sincerely apologies for displaying exponential, logarithmic, and trigonometric functions which i pulled out of my a-hat. And Finally Fifth: The square bracketed [Mass], [Length], and [Time] will be discussed shortly in section "OK, Physics" subsection "What does Physics measure?".
then skipping the messy Algebraic steps to resolve a nice and neat equation. Fourth: I sincerely apologies for displaying exponential, logarithmic, and trigonometric functions which i pulled out of my a-hat. And Finally Fifth: The square bracketed [Mass], [Length], and [Time] will be discussed shortly in section "OK, Physics" subsection "What does Physics measure?".

"Physics Speech" is consistently understandable from the Indisputably Obvious to the Furthest Edge
With sufficient awareness of how the world works I will find a recipe for ambient temperature superconductors, an "electron hill" which is a material in a state of equilibrium that maintains an electrical potential of 240 volts at 100 amperes, and build a Warp Drive.
Coordinate Systems
Physics is an experimental science. The numerical measurements produce vast amounts of data which need to be organized so patterns can be discerned. Graphing the data is a powerful method to illuminate patterns. Each data point on a graph is a group of two or more measured quantities. Each point is a coordinate of the graph. If no data is plotted on a graph, the graph still has an axis or two.
You are Here
Starting with a position one is confronted with the concept of something being "Over There". Beginning with a position and nothing came before this position I can go "Over There" I can come back to the original position. Being lazy and a poor typist I call the original position the "origin". In fact I can be at the the origin with out even having to go "Over There" right from the beginning. Recall the concepts of "neighbourhood" and "continuous" are a result of "a path not taken". They apply here. Two result are equally valid and both illustrate the meaning of "between".
There is a direction that starts from the origin that goes to "Over There" and beyond forever such that "Over There" is between the origin and forever. This mathematical structure is called a ray. There is over two thousand years of properties and implications concerning the ray and forever. Case in point, forever leads to the concept of infinity, ∞, which helped push the mathematician Georg Cantor (1845-1918) over the edge. This alluring path will be a path not taken.
Well, Just a few Steps
The structure at hand is a directed ray from zero to infinity, specifically from zero to positive infinity. By putting a little arrow over the variable x the shorthand, ![]() is read as "the vector x has an inclusive range of zero to positive infinity". So a vector has a length and a direction.
A vector retains the direction even when the length is zero. Now that I think of it, a vector of length zero is not that strange.
is read as "the vector x has an inclusive range of zero to positive infinity". So a vector has a length and a direction.
A vector retains the direction even when the length is zero. Now that I think of it, a vector of length zero is not that strange.
Consider the function that provides the general definition for the position of an object
.
The first derivative defines the velocity,.
The second derivative defines the acceleration,, where a sub x is a vector has a magnitude of a pointing in the x direction.
The third derivative defines the acceleration of the acceleration and is called the jerk,. The derivative is not talked about in polite company, but it does serve to illustrate the point about vectors of zero length.
It can be argued in some circles that what I just said about "the jerk" is incorrect. That the direction of the acceleration vanishes upon applying the derivative to the second derivative for the position of an object. This leaves behind a scalar having a magnitude of zero. My conservative argument is to agree that the magnitude does indeed become zero and the direction does vanish with the resultant scalar poised to take on the vector property of direction and when it does it is a vector of zero magnitude. This crazy idea is to say that zero is unstable and there is something to be said about nothing. Truth be told, there is more to be said about "Nothingness is Unstable" and "Zero is a meta-stable state".
The length of a vector is called the magnitude of a vector. A magnitude without a direction is called a scalar. These are two different objects that have specific properties and usefulness to hold the Physical world together. You can compare apples and oranges with scalars.
Fruit Stand Entrepreneurs
Two friends are walking into town one day having an equal but limited number of pennies in their pockets. One needs a bit more money to make a purchase of some item for an experiment that would advance her understanding of Physics. The other fancies himself a businessman, considers his pennies as Capital and would only invest them for a reasonable return. As they come to a roadside Pick-Your-Own Orchard the sign reads, " Apples and Pears 16 cents, Nectarines and Oranges 24 cents".
"Ha", snorts the young capitalist, "I know four brothers, well actually two sets of twins, that would pay 20 cents for apples and pears, and 32 cents for nectarines and oranges. Odd ducks they are".
After a short pause to consider,
Available Money = 200 cents sub physicist + 200 cents sub capitalist = 400 cents
Cost per Apples and Pears = 16 cents each
Cost per Nectarines and Oranges = 24 cents each
Revenue per Apples and Pears = 20 cents each
Revenue per Nectarines and Oranges = 32 cents each
Profit per Apples and Pears = 4 cents each
Profit per Nectarines and Oranges = 8 cents each
the physicist responds, "I have two dollars and you have the same. Lets pick 16 Oranges to sell at eight cents over cost, one apple to sell at four cents over cost and both make 66 cents".
"Well, that is the most profit we can make given what you know so far", agreed the capitalist. "These brothers are odd. You see each one only prefers one kind of fruit and not one will purchase any unless their brothers purchase the same amount according to his liking. I will invest in your venture providing you agree to three conditions". He paused for dramatic effect and the physicist sighed at this affectation. "You calculate the number of apples, pears, nectarines, and oranges to purchase, you pick the fruit while I recline under this tree, and upon returning my capital give me 25% of the profit".
The physicist agreed to the arrangement as was her custom concerning business dealing with him and picked up a stick to draw in the sandy shoulder of the road.
"Constrain one is money", she said, knowing he wasn't listening anymore
, 16 times A plus P plus 24 times N plus O equals 400
"Simplify this"
, 16A plus 16P plus 24N plus 24O equals 400
"Constrain two, would have been nice to know this at the out-set"
, A equals P equals N equals O equals x
"They all have the same units, yep Fruit is an age old legitimate unit"
, 16x plus 16x plus 24x plus 24x equals 400
"Add together all the x-es"
, 80x equals 400
"Divide both sides by 80"
, 80x over 80 equals 400 over 80 equals x equals 5
"Will this get me enough money for the Blacksmith?"
, 4 times A plus P plus 8 times N plus O equals Profit
, 4 times 5 plus 5 plus 8 times 5 plus 5) equals Profit
, 4 times 10 plus 8 times 10 equals 120
"25% for the venture capitalist is 30 cents", which caused her friend to stir from under the tree,
Satisfied that she would secure sufficient funds for her experiment, the physicist set off to pick five fruits of each kind. Idly she mused, "I wonder if the odd brothers will per chance pay a better price for the odd number of fruits".
So that's how Scalars are used, well, most of the time
The operators addition, subtraction, multiplication, and division are defined for the scalar on a ray, remember ![]() vector x has an inclusive range of zero to positive infinity, and illuminates another mathematical structure called a line. It was discovered that there can be a negative "Over There" such that 0 is between it and a positive "Over There". The range of a line is found to be from negative infinity
vector x has an inclusive range of zero to positive infinity, and illuminates another mathematical structure called a line. It was discovered that there can be a negative "Over There" such that 0 is between it and a positive "Over There". The range of a line is found to be from negative infinity ![]() to
to ![]() positive infinity. The Line is a 1-Dimensional Space and the ray is a special case of a Line called a Half-Line. Three operations on vectors that are consistent in this 1-D Space are addition, subtraction, and multiplication by a scalar. "Which came first, the vector or the scalar"? Go wander around in Set Theory and Number Theory. Be sure to bring Bread Crumbs and 50 feet of rope.
positive infinity. The Line is a 1-Dimensional Space and the ray is a special case of a Line called a Half-Line. Three operations on vectors that are consistent in this 1-D Space are addition, subtraction, and multiplication by a scalar. "Which came first, the vector or the scalar"? Go wander around in Set Theory and Number Theory. Be sure to bring Bread Crumbs and 50 feet of rope.
Coordinate Systems: We have 1; Lets go for 2
Each position on a line has the same properties of every other position on the line. Observation of a line is an interaction with the line and can manifest as a coordinate system.
Recall that I have no answer to the question "Are Stuff and Interaction two things?" though I might pursue that line of inquiry at a later time. I am content with a 1-Dimensional Coordinate System such as it is.
Observe the line from negative infinity to positive infinity ![]() , which is also a Set of all the number between and including the objects negative and positive infinities.
, which is also a Set of all the number between and including the objects negative and positive infinities.
Incidentally, I thought it would be cool to eat Date. I had watched numerous movies about ancient Rome and Greece, mythology, gods and heroes, histories and documentaries. So i purchased a Date Wheel and acquired a taste for the sticky sweet fruit. I still think it is cool to eat dates and I like them, but i do not eat them anymore. Similarly, I thought the symbols of Set Theory and Logic were cool.
Within those forms of arcane glyphs were some mysterious truth I thought. I have found that there are several Set Theories. Each have their utility to communicate ideas. All have axioms, which are nothing more than a really good guess about something that is then taken as a given fact. Many have internal references than neatly bind up a circular argument and some have paradoxes that their children theories try to resolve. I still find Set Theory and Logic cool but to safe guard my own sanity I tend to use it as a shorthand to describe objects and relationships. I only speak it as a broken language to glean out concepts that are on the edges of my own understanding.
Anyway, back to the line from negative infinity to positive infinity ![]() , which is also a Set. Pick a position to be the origin. Let the origin be zero, O = 0. Label this set X with elements from negative infinity
, which is also a Set. Pick a position to be the origin. Let the origin be zero, O = 0. Label this set X with elements from negative infinity ![]() to
to ![]() positive infinity where the element x = O x = 0, O sub x being an explicit label indicating that O is a member of set X with the unique value of zero. This can be written as
positive infinity where the element x = O x = 0, O sub x being an explicit label indicating that O is a member of set X with the unique value of zero. This can be written as
![]() , and read as "Set X equals elements x is greater than or equal to negative infinity and less than and equal to positive infinity where there exists O sub x, an element of X such that x equals zero". This is a mouthful of words needed to translate a handful of symbols.
, and read as "Set X equals elements x is greater than or equal to negative infinity and less than and equal to positive infinity where there exists O sub x, an element of X such that x equals zero". This is a mouthful of words needed to translate a handful of symbols.
Create another set of identical form and label it Y,
![]() .
.
Construct the union of X and Y, where the intersection of X and Y is uniquely defined by the ordered pair (x, y) as the origin where x = y = 0 for all ordered pairs,
![]() .
.
This statement defines the Origin of a general 2 Dimensional Space. The Origin is a specific Ordered Pair whose utility to organise and analyse physical phenomena is widely exploited.
All other ordered pairs (x, y) exist in this 2-D Space and define a surface in this general case. Technical speaking the the set of ordered pairs, call it S, could exist in a 1 dimensional physical space and appear to have 2 dimensions in what I can call a Label Space. For example, I am Jim and James in the same space that my body occupies.
So, a single physical object can have multiple Labels. The union of X and Y equals the ordered pair elements of set S, ![]() , defined by all values of x from negative to positive infinity and all values of y from negative to positive infinity for all x, y ordered pairs.
, defined by all values of x from negative to positive infinity and all values of y from negative to positive infinity for all x, y ordered pairs.
The physical element in set X having the value of zero and set Y having the value of zero is the same object with several labels including the element label of the ordered pair in set S,
![]() . All the ordered pairs that are the elements of the set S are unique labels that map into unique physical locations. From the discussion thus far, set X maps into a 1-D physical space, set Y maps into a 1-D physical space, X and Y have one point in common and all other element map into unique locations. The two lines that correspond to the sets X and Y define a neighbourhood of space where two lines intersect at one and only one point. Essentially, intersect two 1 Dimensional Spaces to produce the state of a 2 Dimensional Space when the intersection is one point.
. All the ordered pairs that are the elements of the set S are unique labels that map into unique physical locations. From the discussion thus far, set X maps into a 1-D physical space, set Y maps into a 1-D physical space, X and Y have one point in common and all other element map into unique locations. The two lines that correspond to the sets X and Y define a neighbourhood of space where two lines intersect at one and only one point. Essentially, intersect two 1 Dimensional Spaces to produce the state of a 2 Dimensional Space when the intersection is one point.
To organise and analyse physical phenomena it is convenient to define or rename set X in terms of ordered pair elements of set S as, ![]() , being the x-axis. Define or rename set Y in terms of ordered pair elements of set S as,
, being the x-axis. Define or rename set Y in terms of ordered pair elements of set S as, ![]() , as the y-axis.
, as the y-axis.
Experimental Evidence Trumps Theory
Data expresses the way it it. The "Way it is" is really what is going on and if a theory fails to be consistent with what is really happening it must be refined. Now, data can also be refined by additional experimental observations. Take a moment and look around at the environment. There might be floors, walls, ceilings; buildings and streets; hills, rivers, fields and lakes, but generally the Earth is flat. This observation has stood the test of time. Yes, the underlying concept of a Flat Earth was refined when it was observed that when Tall Ships are first observed at a great distance, it is their mast which is seen protruding from the ocean's horizon followed by the deck then hull. The refined theory of a Spherical Earth is consistent with the Observations of a locally Flat Earth.
The properties of a Curved Geometry, in the spherical case of the Earth, reduce to Flat Geometry in a small enough neighbourhood as a suitable approximation for utility. To define a Flat Geometry from the Set and Vectors it is useful to use the observations from the Flat Earth knowing full well that this will lead to Curved Geometry. The utility of curved geometry will be apparent if I mention a few observations which guide the refinement of Theoretical Physics.
When Christopher Columbus (1451 – 1506) under the auspices of the Catholic Monarchs of Spain completed four voyages across the Atlantic Ocean, he believed the Earth to be pear shaped and that he had sailed uphill from Europe to the Americas. Well, he was pretty much right, the rotation of the Earth causes it to bulge at the Equator and the greater mass of the Northern Hemisphere pulls the surface closer to the center of the Earth compared to the watery Southern Hemisphere. The distortion isn't much from spherical but is due to gravity, the distribution of matter and angular momentum. So I'm back to the notion of Stuff and Interaction being two things or the dynamics of one thing. Jumping backwards, sideways, and forward from the Columbus Voyages Event are found the relevant pieces of Logic, Geometry, relativity, Newtonian Mechanics, and General Relativity. I can't stop myself from mentioning springs, Maxwell's equations, Special Relativity, and Quantum Mechanics. Yes, springs, those little coils that you compress when you wide up a toy, or click a pen, or smooth the ride in a car or bus.
The point being this
Abstract mathematical concepts have an internal consistency that reflects the Physics of this particular Universe when you plug in some non-theoretical data from experimental observation. The theory that relies on the minimal number of observed measurements and accurately predicts the most parts of what really is going on is the best Theory.
When Last we left our Coordinate Systems
The x-axis and y-axis did not have a definite orientation in 2-Dimensional space. They define a 2-D surface but I want it easy to work with and extensible to map higher dimensions and the underlying properties of Quantum Mechanics and General Relativity that manifest in our Classical Universe. Our everyday experiences are Classical, so intuition is valid and tells us "What it is". When Theoretical Physics is taught it is said to be strange with difficult concepts that only the Mathematical Adept can understand. I want to thwart this impediment but have found that some choices I make to introduce a line of reasoning appears to be pulled out of thin air. This is not the case, as i move forward into the underlying structure hindsight will provide the rationale for the choices.
The y-axis goes up and down; the x-axis goes right and left
Pythagoras (570 – 495 BC) and Euclid (323–283 BC) drew their insights from the Flat Earth on which they lived. Literally, Euclid drew a flat geometry which is used today and is a consistent reduction of higher dimensional geometries. The x-axis and y-axis intersect at one point and are perpendicular to each other. They extend to infinity in a 2 dimensional surface that extends to infinity called a plane in the flat Euclidian Geometry. The reality of this abstract mathematical concept involving infinities come from observations of the Physical World credited to Pythagoras. The Pythagorean Theorem describes the relationship of the length of the sides of a flat 2-dimensional triangle where two sides of the triangle are perpendicular to each other. This type of triangle id commonly called a right triangle.
In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle)
where the x-axis and the y-axis are parallel to the legs and (0, 0) to (x, y) is the hypotenuse. Parallel lines in the flat Euclidian Geometry never intersect each other and are always equidistant from each other. Euclidian Geometry is rather rigid and none interaction with the Physical Environment, this idea of Absolute Space persisted for centuries, has its utility in today's physics and can be enhanced to incorporate additional observations as science advances. The "Enhanced Geometries" of today's physics validate Euclidian Geometry as a special case of their own general features. I will endeavour to keep mathematical abstractions relevant to measurable Physics. Some concepts will render a clearer understanding of the World while others will highlight difficulties in our current theories. This is just "the way it is" right now.
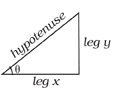 The lines leg y and leg x are perpendicular if the sum of the squares of the lengths are equal to the square of the length of the hypotenuse. This property of the right triangle is a property of all distances in Euclidian Geometry. This property is what makes this geometry flat. Any right triangle,
The lines leg y and leg x are perpendicular if the sum of the squares of the lengths are equal to the square of the length of the hypotenuse. This property of the right triangle is a property of all distances in Euclidian Geometry. This property is what makes this geometry flat. Any right triangle,  illustrates the relationship between the legs and hypotenuse,
illustrates the relationship between the legs and hypotenuse, ![]() . Notice that the illustration and the algebraic equation bear no reference to a coordinate system. Think of it this way, the properties of Set Theory and Geometry introduce thus far lend themselves to the development of a coordinate system. The Origin of the coordinate system can be placed anywhere in the Mathematical Space. All Ordered Pairs,
. Notice that the illustration and the algebraic equation bear no reference to a coordinate system. Think of it this way, the properties of Set Theory and Geometry introduce thus far lend themselves to the development of a coordinate system. The Origin of the coordinate system can be placed anywhere in the Mathematical Space. All Ordered Pairs, ![]() , have the same properties and I will constrain those properties to qualities observed in the Physical World. The Origin of a coordinate system is moved to wherever an observation is made. The results of an observation are not dependent on the coordinate system but are dependent on the space in which they are made. Our Universe exists in a Non-Euclidian Space, but it is easier to see the implications and grasp the non-intuitive concepts if I build upon Euclidian Space born of experimental observations in Physics.
, have the same properties and I will constrain those properties to qualities observed in the Physical World. The Origin of a coordinate system is moved to wherever an observation is made. The results of an observation are not dependent on the coordinate system but are dependent on the space in which they are made. Our Universe exists in a Non-Euclidian Space, but it is easier to see the implications and grasp the non-intuitive concepts if I build upon Euclidian Space born of experimental observations in Physics.
Lines of reasoning and two sides of the same coin
The x,y coordinate system which is trying to define the 2-dimensional space is actually plucking out properties of the 2-D space so I can talk about the space, stuff it contains and the interactions within that environment. The reality is that the Space is independent of the coordinate system. The "Laws of Nature" are independent of the methods used to measure and analyse phenomena. It is a question of looking for the best fit and ensuring that the current "best fit" can be enhanced but further observation and understanding.
Combining the Pythagorean Theorem, derived by observing Stuff, with the Derivative underpinning Calculus, derived by observing Interactions,
Physics reveals a Geometry of the Observable Physical Universe. I understand this geometry to have a Reality separate from the abstract mathematical conceptions of my own thoughts. This being the case, the Flat, Continuous, Two-Dimensional Plane of Euclidian Geometry consisting of an infinite set of lines parallel to the y-axis and an infinite set of lines parallel to the x-axis 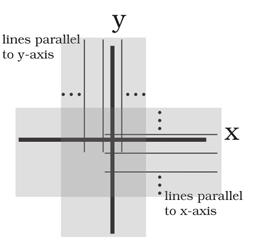 is subject to change. It can only change to become a better Model of the Geometry of the Observable Physical Universe, which is Energy manifesting as Space and Time. Space and Time are emergent properties of the the preexisting energy which imparts energy of our universe.
is subject to change. It can only change to become a better Model of the Geometry of the Observable Physical Universe, which is Energy manifesting as Space and Time. Space and Time are emergent properties of the the preexisting energy which imparts energy of our universe.
The questions of what happened before the Big Bang or is the universe continuously banging or is the universe only one universe in a multiverse are currently debatable and to a point are answerable. Modern Theoretical Physics is a work in progress where the words of abstract mathematical concepts have a Reality supporting our perceptions.
Calculus, Algebra, Geometry, Trigonometry: Much of the Foundation is in Place
I started with a limited introduction to Calculus because it is a very useful language for describing the positions of material objects. Using some algebraic manipulations a description of forces and interactions can be understood. With some basic concepts of Calculus in hand, I drifted into Set Theory and Geometry in an attempt to show that the notion of Neighbourhood and Continuous are common properties to these three branches of mathematics. It is hoped that the logical underpinning and organization of Physics (Reality) are reflected in Mathematics (Concepts).
The x-axis and y-axis can be considered two basis vectors associated with the two sets containing the scalar values from negative to positive infinity. A basis vector is a vector having a direction and a length of one unit, also called a unit vector, and provides a fundamental element to describe the space in which it is placed. In a two dimensional space there are two basis vectors ![]() . Consider ice cream for a moment. It comes in a variety of flavours; chocolate, vanilla, and strawberry to name three. When these three flavours are placed side by side in a single container it is often referenced as Neapolitan Ice Cream. The name "Neapolitan Ice Cream" encapsulated the flavours and orientation of the ice cream within the container. It is a shorthand expression that replaces a mouthful of descriptive words. Simply put, the set of two basis vectors encapsulates all the properties described thus far and is called a tensor. This tensor is consistent with all the piecemeal mathematics that is currently taught and understood. It is a very short shorthand for a mountain of books. There are more concept stuffed into this tensor that I have not mentioned. The concepts I am concerned with are those that have Physical Reality in our Universe. I will not work through mathematical proofs. My assumptions and interpretations are based on what is perceived and measured.
. Consider ice cream for a moment. It comes in a variety of flavours; chocolate, vanilla, and strawberry to name three. When these three flavours are placed side by side in a single container it is often referenced as Neapolitan Ice Cream. The name "Neapolitan Ice Cream" encapsulated the flavours and orientation of the ice cream within the container. It is a shorthand expression that replaces a mouthful of descriptive words. Simply put, the set of two basis vectors encapsulates all the properties described thus far and is called a tensor. This tensor is consistent with all the piecemeal mathematics that is currently taught and understood. It is a very short shorthand for a mountain of books. There are more concept stuffed into this tensor that I have not mentioned. The concepts I am concerned with are those that have Physical Reality in our Universe. I will not work through mathematical proofs. My assumptions and interpretations are based on what is perceived and measured.
The 2-Dimensional space is a 2-D vector since X and Y are both 1-D vectors defining the ordered pair which technically is ![]() but the "e hat" vector notation generally is dropped. The variables x and y in the ordered pairs are scalars multiplied by what are called the basis vectors ê x and ê y of the Cartesian Plane. The distance to any point on the plane from the Origin is given by the magnitude of the vector with its Tail at the Origin and its Head at the Coordinate (x, y). From the Pythagorean Theorem
but the "e hat" vector notation generally is dropped. The variables x and y in the ordered pairs are scalars multiplied by what are called the basis vectors ê x and ê y of the Cartesian Plane. The distance to any point on the plane from the Origin is given by the magnitude of the vector with its Tail at the Origin and its Head at the Coordinate (x, y). From the Pythagorean Theorem
In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle)
where x and y are the legs and (0, 0) to (x, y) is the hypotenuse, call it s, ![]() . Writing the relationship as
. Writing the relationship as ![]() looks better on the page and means the same thing. If s = 1, then x2 + y2 = 1 defines a set of coordinates called the unit circle with center at (0, 0). The nice thing about 2-space is 2-D objects can exist. A vector having a magnitude of 1 with its tail at (0, 0) has its head on the circumference of the circle and is called the radius, r, of the circle. With the tail of vector r remaining at (0, 0) the head can start at (1, 0) and rotate counter-clockwise through (0, 1), (-1, 0), (-1, -1), and back to the initial orientation (0, 1). From the Pythagorean Theorem the length of the circumference is c = 2πr. So rotating an object through an angle of 360°, also written as ∠ 2π radians, returns an object to the initial orientation.
looks better on the page and means the same thing. If s = 1, then x2 + y2 = 1 defines a set of coordinates called the unit circle with center at (0, 0). The nice thing about 2-space is 2-D objects can exist. A vector having a magnitude of 1 with its tail at (0, 0) has its head on the circumference of the circle and is called the radius, r, of the circle. With the tail of vector r remaining at (0, 0) the head can start at (1, 0) and rotate counter-clockwise through (0, 1), (-1, 0), (-1, -1), and back to the initial orientation (0, 1). From the Pythagorean Theorem the length of the circumference is c = 2πr. So rotating an object through an angle of 360°, also written as ∠ 2π radians, returns an object to the initial orientation.
The equation ![]() of the Pythagorean Theorem is the equation for the distance between any two points in the space. The distance equation is called the metric. In a Flat Space or a small enough neighbourhood of a Curved Space it can be a rather simple equation. One of the things I really like about this metric is that when I go from 2-D space to 3-D space I only have to add another term, call it z,
of the Pythagorean Theorem is the equation for the distance between any two points in the space. The distance equation is called the metric. In a Flat Space or a small enough neighbourhood of a Curved Space it can be a rather simple equation. One of the things I really like about this metric is that when I go from 2-D space to 3-D space I only have to add another term, call it z, ![]() . To bring along all the properties of a third coordinate the tensor
. To bring along all the properties of a third coordinate the tensor ![]() also needs another term,
also needs another term, ![]() . The three coordinate axes are perpendicular to each other and all is fine,
. The three coordinate axes are perpendicular to each other and all is fine, ![]() . So accounting for additional dimensions is not big deal and you can do a lot with four. It is completely reasonable that time is a fourth spatial dimension,
. So accounting for additional dimensions is not big deal and you can do a lot with four. It is completely reasonable that time is a fourth spatial dimension, ![]() , perpendicular to the intuitive three dimensions of height, width, and depth.
, perpendicular to the intuitive three dimensions of height, width, and depth.
Since a brought up the topic of 3-D Space and said that mathematics is consistent among branches of mathematics, I want to mention something I just noticed. The formula to calculate the volume V of a sphere having a radius r, ![]() , is four thirds pi r cubed. The derivative of this equation gives the surface area of the sphere,
, is four thirds pi r cubed. The derivative of this equation gives the surface area of the sphere, ![]() , as four pi r squared. This is a very nice thing because it helps tie together many physical phenomena. Two words of caution will follow the next revelation I had. The formula to calculate the area A of a circle having a radius r,
, as four pi r squared. This is a very nice thing because it helps tie together many physical phenomena. Two words of caution will follow the next revelation I had. The formula to calculate the area A of a circle having a radius r, ![]() , is pi r squared. The derivative of this equation gives the circumference of the circle,
, is pi r squared. The derivative of this equation gives the circumference of the circle, ![]() , as two pi r. This is also a very nice thing because it helps tie together many other physical phenomena. The first word of caution is to be aware of what is being measure and how the calculation is being interpreted. The second word is that the relationship between a circle and a sphere is not as simple as intuition seems to promise which opens up a Can of Worms called Group Theory. On the other hand, The bizarre objects and operations of Group Theory render to physical stuff and interactions. Peel back the onion skin of our Classical World and we will find Real really existing particles, waves, fields, uncertain point particles, loops of energy, strings, knots of space and time, or something that Real really exists.
, as two pi r. This is also a very nice thing because it helps tie together many other physical phenomena. The first word of caution is to be aware of what is being measure and how the calculation is being interpreted. The second word is that the relationship between a circle and a sphere is not as simple as intuition seems to promise which opens up a Can of Worms called Group Theory. On the other hand, The bizarre objects and operations of Group Theory render to physical stuff and interactions. Peel back the onion skin of our Classical World and we will find Real really existing particles, waves, fields, uncertain point particles, loops of energy, strings, knots of space and time, or something that Real really exists.
I have to reign it in and finish this Math to apply it to Physics
A Closer look at Vectors
Consider the set X which has a basis vector of length one and scalar values from -∞ to +∞, X = { ê x ∧ -∞ < x < +∞}. For all scalars a, b, c, and d in X the following operators are defined
a + b = b + a = c
a × b = b × a = ab = ba = Σ 1b a i = Σ 1a b i = d
"multiplication is addition done many times for integers, the sigma, Σ, is a symbol for summation
Σ 1b a i = a 1 + ... + a b, where b ≠ 0 and Σ 1b a i = 0 where b = 0"
a × 0 = 0 × a = 0
a × 1 = 1 × a = a
b × (-1) = -b
a - b = a + ((-1) ×b) ≠ b - a = b + ((-1) ×a), ∀ a ∧ b, "for all a and b"
"subtraction is addition of a negative number and is non-commutative"
d / a = b, where a ≠ 0 and d / a = 0, where a ≠ 0 and d = 0
"d/a can be an integer, fraction, rational, irrational, computable, 'more numbers, than are dreamt of in your philosophy', and numbers named due to their virtue fundamental to the universe such as π"
"the scope of multiplication as defined by the Σ operator is actually broader due to the ramifications of division and the basic concept remains intact"
Vectors in X = { ê x ∧ -∞ < x < +∞} point in a direction and have a length. The direction of the basis vector, ê x, is that direction. The length of ê x is the scalar value 1.
1 × ê x = ê xThe vectors a, b, and c are all parallel to each other and the magnitude of a vector exists in the range of (0, +∞).
a × ê x = aê x
aê x + bê x = (a + b)ê x = cê x, where a + b = c
"graphically the head of a is placed at the tail of b and the length of c is from the tail of a to the head of b"
(-1) × ê x = -ê xmeans that -ê x is anti parallel to ê x. If ê x points in that direction, then -ê x points in the other direction. To be consistent with the mountain of mathematics climbed so far multiplication of a vector by -1 rotates the vector through an angle of 180°, also written as ∠π radians.
aê x - bê x = (a - b)ê x = cê x, where a - b = c
"graphically the head of a is placed at the tail of b and the length of c is from the tail of a to the head of b"
Think of rotates through an angle in a 1-space as quantum mechanical states where ê x points ∠ 0 and -ê x points ∠ π with nothing between.
Vector Multiplication comes in Two Forms
The Pythagorean Theorem, "In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle)" defines the relationships of the component magnitudes of a right triangle in 2-D space.
hypotenuse xy2 = leg x2 + leg y2In 1-D space leg y does not exist and the relationship reduces to hypotenuse x2 = leg x2 This relationship gives rise to the useful definition of Absolute Value
|x| ≡ √x2Interestingly, |hypotenuse| = |leg x| = |h| = |xê x| for a 1-D triangle for xê x directed ∠ 0, parallel to ê x, and xê x directed ∠ π, anti parallel to ê x. By considering all the mathematical properties, spaces, structures, and operations discovered thus far, it is reasoned that ratio
leg x, the leg adjacent to ∠ 0 or ∠ πis proportional to ∠ 0 or ∠ π in a significant and fundamental manner.
-----------------------------------------
hypotenuse x
x
--- ∝ ∠ θ
h
", where θ = 0 and π in 1-space and θ = (0, +∞) in 2-space"
This is the bare minimum to define one form of vector multiplication, called the dot product.
x
--- = cos θ
h
a ⋅ b ≡ |a| |b| cos θIn 2-space, a plane, vectors a and b can have an angular separation of any arbitrary value of θ. Recall that a rotation of ∠ 2π returns an object to its initial orientation, not surprisingly the range of the cosine function exhibits the same nature. Reducing the domain θ from (-∞, +∞) to 0 ≤ θ ≤ 2π maintains the full set of the range -1 ≤ cos θ ≤ 1. Cosine is a periodic function having a period of 2π.
No matter what the angle between a and b is, b can be written as the sum of two vectors that are perpendicular and parallel to the vector a
b = b ⊥ê a⊥ + b ¶ê a¶The Dot Product can be calculated from ordered pairs in a Cartesian Plane. Since each (x, y) coordinate is a vector with its Tail at the Origin and the Head at the point (x, y) where x is the projection onto the x-axis and y is a projection onto the y-axis.
"the parallel part, b ¶ê a¶ is called the projection of b onto a and equals"
|b| cos θ
"in the definition of the Dot Product"
For any two points (a x, a y) and (b x, b y)This pattern of the Dot Product extends to 3 and higher dimensional spaces.
a ⋅ b = a xb x + a yb y
a ⋅ b = (a x, a y, a z) ⋅ (b x, b y, b z)
a ⋅ b = a xb x + a yb y + a zb z
Vectors are used extensively in Physics such as Work which is defined as the scalar product of force and displacement.
A Coordinate System in 3-Space to Finish Vector Multiplication
1-D Space
X = { ê x ∧ -∞ < x < +∞} |O x ∈ X : x = 0
2-D Space
X = { ê x ∧ -∞ < x < +∞} |O x ∈ X : x = 0
Y = { ê y ∧ -∞ < y < +∞} |O y ∈ Y : y = 0
(X ∪ Y) ∩ {O x = O y= 0} ≡ (0, 0) ∀ (x, y)
3-D Space
X = { ê x ∧ -∞ < x < +∞} |O x ∈ X : x = 0
Y = { ê y ∧ -∞ < y < +∞} |O y ∈ Y : y = 0
Z = { ê z ∧ -∞ < z < +∞} |O z ∈ Z : z = 0
(X ∪ Y∪ Z) ∩ {O x = O y = O z= 0} ≡ (0, 0, 0) ∀ (x, y, z)
There is probably a more compact way to write three orthogonal sets of infinite numbered vector spaces but this verbose way maintains the visibility of the base properties. The unit vectors ê x, ê y, and ê z orient the x-axis, y-axis, and z-axis. The coordinated of the unit vectors are
ê x = (1, 0, 0)Using the Dot Product show the 3 axes are perpendicular to each other
ê y = (0, 1, 0)
ê z = (0, 0, 1)
ê x ⋅ ê y ⋅ ê z = (1 × 0 × 0) + (0 × 1 × 0) + (0 × 0 × 1) = 0But, why is the x-axis positive to the right and negative to the left with the y-axis positive in the up direction and negative directed down having the z-axis positive coming out of the page and negative going into the page?
ê x ⋅ ê y= 0
ê x⋅ ê z = 0
ê y ⋅ ê z = 0
ê x ⋅ ê y ⋅ ê z = 0
The result of Vector Multiplication by the Dot Product is a scalar. The Dot Product addresses parallel components of two vectors. The other form of Vector Multiplication is called the Cross Product which resolves to a vector. The Cross Product addresses perpendicular components of two vectors. Starting with the Pythagorean Theorem
hypotenuse xy2 = leg x2 + leg y2The leg of interest is
leg y, the leg opposite to ∠ θThe significant and fundamental proportionality
----------------------------------
hypotenuse xy
yis defined as the periodic function called sine
--- ∝ ∠ θ
h
yThe Cross Product
--- = sin θ
h
a × b ≡ |a| |b| sin θResults in a vector pointing in the right direction. To ensure the direction is correct there are two properties of the Cross operator that need to be addresses, right? The vector product is not commutative
a × b ≠ b × aand the measured angle progresses from the first listed vector to the second listed vector. The left hand side of the equation measures θ from a to b and the right hand side measures θ from b to a, right?
"Truth be told,"
a × b = - b × a
To find the right direction of the resulting vector, take your right hand and wrap your fingers from the first vector to the second vector. Your thumb points in the fight direction. This technique is called, "The Right Hand Rule".
A Coordinate System in 3-Space...
The basis vectors ê x, ê y, and ê z all have a positive magnitude and are perpendicular to each other. The most ergonomic way to draw a line on a page to represent the x-axis and possessing the foreknowledge that "The Right Hand Rule" will be applied to determine the directions of the other two axes is to draw a horizontal line with positive going to the right. This leads to positive y values traveling up the page and positive z values coming out of the page.
...to Finish Vector Multiplication
Calculating the vector product with basis vectors looks algebraically daunting, only because of the bookkeeping. It is worth walking through the operation to build some vector intuition which is very useful in Physics.
The following list of properties are apparent from the concepts described thus fara × b = (a xê x + a yê y + a zê z) × (b xê x + b yê y + b zê z)
= a xb x(ê x × ê x) + a xb y(ê x × ê y) + a xb z(ê x × ê z)
+ a yb x(ê y × ê x) + a yb y(ê y × ê y) + a yb z(ê y × ê z)
+ a zb x(ê z × ê x) + a zb y(ê z × ê y) + a zb z(ê z × ê z)
a × (ab) = (aa) × b = a(a × b)after some concentration
a × (b + c) = a × b + a × c
a × b = - b × a
a × a = 0
ê x × ê x = ê y × ê y = ê z × ê z = 0
ê x × ê y = −ê y × ê x = ê z
ê x × ê z = −ê z × ê x = −ê y
ê y × ê z = −ê z × ê y = ê x
a × b = (a yb z − a zb y)ê x + (a zb x − a xb z)ê y + (a xb y − a yb x)ê zbut this can be written as a determinant that is easy to remember and easy to use. The Determinant comes from Linear Algebra. To set up a determinant and calculate a × b Right Hand System
Multiply diagonal entries together going uphill from right to left for adding
| ê x ê y ê z | a × b = det a x a y a z b x b y b z
+ (b za y)ê x + (b ya x)ê z + (b xa z)ê yMultiply diagonal entries together going uphill from left to right for subtracting
- (b xa y)ê z - (b ya z)ê x - (b za x)ê yCollect the terms
a × b = (b za y − b ya z)ê x + (b xa z− b za x)ê y + (b ya x− b xa y)ê zWhich is the same as the standard algebraic result
a × b = (a yb z − a zb y)ê x + (a zb x − a xb z)ê y + (a xb y − a yb x)ê z
but many fewer steps.
Coordinate Systems: A Last Word for now
Space has properties. A lot of Physics fits into this 3-D Euclidian space. As the need arises other properties of space will be explored. A Coordinate Systems is a mapping onto a space so the tools of mathematics can be used. The Laws of Physics do not depend on the Coordinate System used to express them.
2-D Space
Coordinates are operational functions the relate every point in space to the Origin of a Coordinate System. For a point, P, in a plane Cartesian coordinates are (x(P), y(P)) and Polar coordinates are (r(P), θ(P)).The functions are defined
x(P) ≡ the distance from the y-axis parallel to the x-axis
y(P) ≡ the distance from the x-axis parallel to the y-axis
r(P) ≡ the distance, radius, from the Origin, called the Pole
θ(P) ≡ the counter-clockwise angle, azimuth, from a fixed ray,
called the Polar Axis
and the symbol (P) are dropped from the notation. The placement of the Origin for Cartesian coordinates and Polar coordinates is completely arbitrary as is the orientation of the polar axis. The choice of coordinates is a matter of convenience.
3-D Space
Three convenient coordinate systems used in Physics are
Cartesian (x, y, z)
Cylindrical (ρ, φ, z)x ≡ the distance from the y-axis parallel to the x-axis
y ≡ the distance from the x-axis parallel to the y-axis
z ≡ the distance from and perpendicular to the x-y plane
Spherical (r, θ, φ)ρ ≡ the distance from the Pole and perpendicular the z-axis
φ ≡ the angle from the Polar Axis about the z-axis
"Polar (r, θ) = Cylindrical (ρ, φ, z) where r = ρ, θ = φ, z = 0"
z ≡ the distance from the Pole and parallel to the z-axis
r ≡ the distance from the Pole
θ ≡ the angle from |(Polar Axis)×∠φ|
"that is to say, θ ≡ the angle from the perpendicular projection of the reference plane resulting from the Polar Axis and the angle φ"
φ ≡ the angle from the Polar Axis
with the choice of which to use as dictated by simplicity and clarity of the Physical Processes. When transforming between these coordinate systems it is convenient to set Pole = Origin and Polar Axis = x-axis ≥ 0.
OK, Physics
A body in motion tends to stay in motion and a body at rest tends to stay at rest unless acted on by an external force. Centuries of experimentation to prove or disprove this statement led to the conclusion that the assertion is correct. This observation has stood the test of time and its implications have grown deep roots on Physics.
First Experiment
Imagine sitting in an airplane flying through calm sky at a velocity of 600 miles per hour. Place a coin on the tray-table, then trace its circumference with a pen. lift then coin and drop it several times. It falls straight down and hits the target within the experimental error of the setup.
Second Experiment
Now take the spring out of the pen and an ice cube from the complimentary beverage provided by the airline. Place one end of the spring against the lip of the tray-table. Place the ice cube on the table and at the free end of the spring. Move the ice cube toward the lip of the table to compress the spring. Release the ice cube. In less than half-a-blink-of-an-eye, a very short time indeed, the ice cube is moving across the table.
Repeating this experiment several times and at various angles on the tray-table:
side to side being left to right and right to left, front to back, back to front, corner to far corner, ...
and measuring the speed of the ice cube anywhere along its path just after a "blink" from release to just before colliding with the lip of the table
finds the path of the ice cube to be straight and the speed to be constant within the experimental error of the setup. It is also determined that lighter ice cubes move faster than heavier ice cubes.
Third Experiment
Since the pen is already in pieces place the ink cartridge flat in the table. Balance a rule across the cartage so that it is horizontal and the distance markings are visible. Select two ice cubes such that when each is placed on the rule equidistant from the cartridge the rule remains horizontal. The two ice cubes will have the same weight within the experimental error of the setup.
Forth Experiment
It is possible to set up the ice cube experiment and place the second cube on the table and predict whether or not there will be a collision between the moving and stationary ice cubes. The prediction is not Clairvoyance it is Physics.
Set up the second ice cube experiment such that a collision occurs each time it is repeated and the two cubes remain in contact after the collision. Measuring the velocity of the moving cube before the collision with the stationary cube and then measuring the velocity of the two cubes moving together reveals that the velocity decrease by a factor of two within the experimental error of the setup. Repeating the experiment with the two ice cubes already in contact with each other results in a constant velocity that is equal to the final velocity recorded for the collision experiment.
Image the airplane will be landing soon and being an honourable individual you clean up the mess made on the tray-table. After the airplane lands you await your ride sitting at a restaurant table moving at 0 miles per hour and order a beverage. Repeating the experiments done on the airplane render the same results.
A Handful of Fundamentals
Though the two sets of experiments were done in different environments, the airplane (A) traveling at a velocity of 600 miles per hour and the restaurant (R) traveling at 0 miles per hour, they share important similarities. In both A and R each "tick" of time is the same everywhere. In both A and R all points have the same properties and are uniform in all directions. What, at first glance, looks like the "difference" is actually a similarity. Both A and R are moving with a constant velocity.
The set of "ticks" and "points" moving with constant velocity is called an Inertial Frame.Physics today rests on a foundation of philosophy, history, mathematics, and experimentation. The final arbiter of the Validity of Physics is Experimental Reproducibility. Physics may not be the Truth (Capital "T" Truth) but it points in the direction of what is true (Small "t" truth). Our understanding of the "Laws of Nature" are Physics Equations and subject to refinement. Some fundamental concept may very well be Truly Fundamental while other are truly fundamental in utility and guidance.
When a Coordinate System is mapped onto an Inertial Frame it is called a Frame of Reference.
Safer Physics ≡ retain a "so far so good" attitude and an eye toward Critical ThinkingThe prospect of determining the laws that govern the physical world is based on a centuries old concept.
Principle of Relativity ≡ Physics Equations describing the Laws of Nature must have the same form for any Frame of Reference.This extremely broad definition requires that all the special cases that are derived from it are consistent with each other.
The motion of the airplane (A) can not be detected by an observe in the airplane because the Coordinate System use to make observation is moving with the Inertial Frame A. The same holds true in the restaurant (R) even though Frame R is is moving about 1000 miles per hour relative to the Sun and stars. The coins fall straight down and the ice cubes move in straight lines in both Frame A and Frame R. The dropped coin does not change position along the airplane axis from tail to nose(X A) for the Frame A observer. However Observer R sees the entire Frame A displaced along the Flight Path(X R).
In the restaurant (R), Observer R tracks objects with (x R, y R, z R, t R) and records an airplane(A) flying with a velocity xR. Observer A, aboard the airplane(A), tracks objects with (x A, y A, z A, t A). Both Observers Agree:
Each determines themselves to be at rest and the other is movingObserver R derives the following coordinate transformation:
Lengths are the same for each
Time is the same for each
x A = x R - v xRt R
y A = y R
z A = z R
t A = t R
and gives them to Observer A to review. Both observers conclude that the coordinate transformation is valid when the subscript "R" stands for the "Observer at Rest", not restaurant (R), since each finds themselves at rest and the other is moving. This transformation is old news that stood for about 300 years.
Galilean Transformation
Galileo Galilei (1564 - 1642) treated time as an absolute and equated Reference Frames by four relationships now called the "Galilean Transformation". This was later refined by Hendrik Lorentz (1853 - 1928) due to experimental evidence that an Observer A and an Observer R may measure different distances, elapsed times, and even different orderings of events. The Galilean Transformation is a special case of the "Lorentz Transformation". The Principle of Relativity remains fundamental and valid.
What does Physics measure?
There is a large technical vocabulary used in Physics but a lot can be understood with only three words. In the four experiments
Dropping a coin,in two Frames of Reference several Physical Properties can be determined. The Principle of Relativity is a fundamental truth (Small "t" truth) which can be taken for granted as long as it is not violated by an error in reasoning. Velocity is calculated from a measure of Length[L] and a measurement of Time[T].
Propelling an ice cube to a constant velocity,
Balancing two ice cubes, and
Colliding two ice cubes
A measure of Length can be measured in shorter or longer distances but Length itself is what it is. A measure of Time can be measured in smaller or larger duration but Time itself is what it is. "so far so good"
[L]
-----
[T]Velocity =
In less than half-a-blink-of-an-eye, in the second experiment, the ice cube is moving at a constant velocity. It took a bit of Time for the ice cube to get up to speed. The result of this brief passage of Time is velocity. Something multiplied by Time resolves into velocity. This something is
While the spring was in contact with the ice cube and decompressed it accelerated the ice cube to a velocity which remained constant once the spring was no longer in contact. There is something in the compressed spring that is transferred to the stationary ice cube resulting in an uncompressed spring and a moving ice cube. There is also another something missing just about the ice cube. It the first state it is at rest. In its second state it is in motion. A closer look at history and the other experiments can reveal what this transfer is and what these two "somethings" are.
[L]
---------
[T][T]Acceleration =
For countless ages it has been observed that it takes effort to start an object moving and it takes effort to stop its motion. To understand this need for effort the concept of Inertial Mass [M I] was invented. A concept must be testable and provide valid predictions of events to be accepted in Physics.
The "effort" is provided by the spring where the "transfer" is expressed by force acting on the Inertial Mass of the ice cube. When the ice cube is in contact with the spring, the ice cube experiences and acceleration. Force can be defined in terms of Inertial Mass and acceleration.
The theory states that the force accelerates the ice cube to a constant velocity which is verified experimentally. Since the spring provides an equal amount of force on an ice cube for each repetition of the experiment the theory predicts that changing [M I] will change the velocity in a specific way.
[M I][L]
---------
[T][T]Force =
The resultant velocity is inversely proportional to the magnitude of the Inertial Mass. This is also confirmed in the experiment when it was observed that lighter ice cubes move faster than heavier ice cubes. This line of reasoning and collection of experimental evidence validates the existence of [M I] at least qualitatively.
[M I][L]
---------
[T][T][M I][L]
---------
[T]× [T] =
In the first experiment the coin starts at rest, acquires motion upon release then returns to rest on the table. Holding the coin suppresses its motion until it is released and then the table suppresses the motion again.
The scientific investigation into gravity dates back to at least the 4th century BC. The physics of Aristotle (384 BC - 322 BC) is a philosophy broader in scope than Modern Physics. It set forth principles of change that govern the natural world and laid the foundation of scientific reasoning. Aristotle's concept of gravity was refined by Galileo (1564 - 1642), Isaac Newton (1642–1727), and physicists to the present day.This experiment demonstrates gravity acting on the coin. When released the coin accelerate into a state of motion until it comes to rest again on the table. Centuries of experimentation have determined that all bodies accelerate at the same rate near the surface of the Earth. Yet all bodies do not weigh the same. Gravity is acting on some property of the body. That something about matter is named Gravitational Mass [M G]. Acceleration due to gravity is a property in Space surrounding a body of matter. The acceleration produces motion unless it is restrained by something equal and opposite to the direction of the acceleration. The magnitude and direction is called the
Normal Force = - (Gravitational Mass) × (acceleration due to gravity)thus what we experience as weight is the retarding effect the normal force on the motion of an of a body acted on by the acceleration due to gravity. Without a normal force between the table and the coin, the coin would move though the table at an ever increasing velocity. The concept of Gravitational Mass [M G] is consistent with the principles and calculations based on experimental measurements thus far and it offers a testable explanation of weight. "so far so good" Rearranging the equation for the Normal Force
reveals an equation in the same form which was derived to describe the properties of Inertial Mass [M I].
[M G][L]
---------
[T][T]- Normal Force = Weight = Force =
This formalism explains some observed phenomena. The force needed to hold the coin above the table is the same amount of force the table exerts on the coin when it is lying motionless. This is commonly called weight and specifically called the weight of the coin in this experiment. It appears the acceleration due to gravity acts on [M G] when objects are in contact and at a distance from each other.
The conclusion that the force needed to hold an ice cube motionless in contact with a compressed spring is derived from the measurement of its velocity when it is released. The acceleration experienced by [M I] exists during the brief time of contact with the spring after the effort to hold the ice cube stationary is removed explains why the ice cube moves with a constant velocity. Acceleration stopped when contact stopped.
A strange thought just occurred. Is a Falling Object Weightless? There is no Normal Force acting on the object to give a perception of Weight.
A conclusion can be made from the results of the third experiment that when two ice cubes are in balance on equidistant points from the center of the rule they experience the same amount of Normal force to arrest the motion that the acceleration due to gravity would impart. Their weights are equal and their [M G] are equal. Using the ice cubes from the third experiment in the forth experiment allows the comparison of [M G] to [M I]. After the collision of ice cubes the final velocity of two ice cubes traveling in contact together was found to be half of the initial velocity of the single ice cube traveling alone. When two ice cubes were already in contact and accelerated into motion by the spring their velocity was equal to the final velocity of the collision experiment. Inertial Mass [M I] and Gravitational Mass [M G] appear to be proportional based on the experiments and the theoretical construction of Physics derived thus far.
Centuries of experimentation verify that [M G] = [M I] to an accuracy of about twenty decimal places. That is [M G] = [M I] to one part in a hundred thousand thousand thousand billion which is one part over twenty orders of magnitude which is a ratio of 1 : 1020 which is rather unimaginable. OK, a billion is 109 and light travels about 1 foot in a billionth of a second. A billionth of a second is called a nanosecond, 10-9 second. Global Positioning Satellites (GPS) measure time in nanoseconds to calculate positions on Earth. Modern Physics Equations models this stuff and interactions, but for now... Mass [M] is Mass[M]. It interacts with farces and gravity.
Length[L], Time[T], and Mass[M] are Fundamental for now
The square bracket notation is used to designate dimension with reference to a coordinate system. Length can be measured in feet, meters, or whatever is convenient. Time can be measured in seconds, years, or whatever is convenient. Mass can be measured in slugs, grams, or whatever is convenient. A lot of Physics can be understood by comprehending the relationship of [L], [T], and [M].
Perception and Prediction: Part I
The Observer affects the Observed is consistent with the Principle of Relativity and taken together form a Philosophical Basis of Physics. The truths of Physics are validated by experimental evidence and may well point to the Truth of what the Universe is and how it works. What follows in these sections "Perception and Prediction: Part ..." are interpretations of observations consistent with Physics Equations.
It takes more effort to lift a ball from the ground to a waist high position than to simply support it waist high above the ground. It takes some skill to catch a thrown ball. Sometimes it will sting your hand upon impact but other times it seems to gently come to rest. It both cases after a successful catch you support the weight of the hall in your hand. The weight of the ball remains constant during the interactions yet the ball "feels" different at times. The weight is the force due to the acceleration due to gravity directed towards the ground interacting with the mass of the ball
for short. The "F" and "a" are in bold type to represent vector quantities, having both magnitude and direction. The ball has a different feel when you change its velocity. At the moment you pick the ball up it feels slightly heavier, then "normal", then slightly lighter for an instant when you stop its motion at your waist. You accelerated it into motion, "heavier", and decelerated it to a stop, "lighter", while most of the time it felt normal. The sensation of heavier and lighters more dramatic if you have the opportunity to take a freight elevator from say the Loading Dock up to the third or forth floor.You will feel heavier when it starts and lighter when it stops while feeling motionless when traveling upwards at a uniform speed.When you catch a ball by stopping it quickly it can sting your hand. If you cradle the ball during the catch it stops more slowly and you do not hurt your hand.
[M][L]
---------
[T][T]F = ma =
We seem to have an intuitive perception of acceleration, velocity, and force. We also have a lot of words to describe these three thing, so many in fact that it would make Physics sloppy. Acceleration and decelerated are simply referred to as acceleration. Velocity is a vector which has a magnitude called speed. Say a race car is traveling on a mile long circular track. It completes a lap every 18 seconds, so it has an average and instantaneous speed of 200 miles per hour because speed has no directional component. Its average velocity per lap is zero because the directional component rotates 360° with each lap and sums to zero per lap. Note of caution: The instantaneous velocity at every point on the car's path of 200 miles per hour. Check both vectors before crossing the track.
The way the ball "feels" is related to it mass and velocity which is called momentum, specifically linear momentum
and the change of momentum is felt as a force. Note that "lifting" the ball from the floor and "impact" of the ball when catching it are two different words but in physics are the same word, "force".
[M][L]
-------
[T]p = mv =
Newton's Laws of Motion are mathematical expressions of perception experimentally verified by Physics. By the IOTTMCO Theorem
The IOTTMCO Theorem ≡ Intuitively obvious to the most casual observer
Newton's First Law: Every object will remain at rest or in uniform motion in a straight line unless compelled to change its state by the action of an external force.
Newton's Second Law: The rate of change of momentum, acceleration, produced by a particular force acting on a body is directly proportional to the magnitude of the force, inversely proportional to the mass of the body and in the same direction of the particular force.
Newton's Third Law: To every action there is always opposed an equal reaction; or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts. "For every action there is an equal and opposite reaction."
but, it is not warranted to use such a Powerful Mathematical Theorem.
A Closer Look at Newton's Laws of Motion
The support for these three laws can be found in the preceding words of this paper which draws from multiple sources including
Philosophiæ Naturalis Principia Mathematica, Latin for "Mathematical Principles of Natural Philosophy", often referred to as simply the Principia, is a work in three books by Sir Isaac Newton, first published 5 July 1687. After annotating and correcting his personal copy of the first edition, Newton also published two further editions, in 1713 and 1726. The Principia states Newton's laws of motion, forming the foundation of classical mechanics, also Newton's law of universal gravitation, and a derivation of Kepler's laws of planetary motion (which Kepler first obtained empirically). The Principia is "justly regarded as one of the most important works in the history of science".such that
http://en.wikipedia.org/wiki/Philosophi%C3%A6_Naturalis_Principia_Mathematica
Newton's First Law: p = mv
Newton's Second Law: F = ma
Newton's Third Law: F 12 = - F 21
is comprehensible within the scope of this paper.
This Should Really Be A Footnote: E1
What is work? Something you do to make money. Something you do to make a change. The active effort to stop a change from happening. I worked as a Nurse for more than two decades, it did not seem like work most days because I enjoyed it. Perception along with the observed effecting the observer slips into the definition of work. Work is the observed effect of effort. Among the many definitions of work there are consistencies that "work" in Physics. The effort of the spring makes a change on the ice cube. The work, W, done by the spring is the result of the force, F, effecting the ice cube during the contact distance, d, producing motion in the direction parallel to F and d. Work does not have a direction. It is a positive magnitude indicative of what is interesting to the observer.
W = Fd
the dimensions of mechanical work
[M][L][L]
-----------
[T][T]W = Fd =
and the scalar product of two vectors is governed by mathematical reasoning
w = F⋅d ≡ |F| |d| cos θ = F xd x + F yd y + F zd z
the Dot Product.
The choice of coordinates is a matter of convenience made by the observer. The use of square bracket has introduced the field of Dimensional Analysis. This field will be explored further as needs in Physics arise.
This Should Really Be A Footnote: E2
What is energy? The ability to do work. The follow up question, "But, what is it?" usually elicits a rather long list including: acoustic, chemical, elastic, electric, gravitational, luminous, magnetic, mechanical, nuclear, optical, radiant, solar, sound, thermal, vibrational, and mass itself which are all forms of energy. They come with their own units of measurement, some of the words in the list have overlapping meanings and some can be divided into sub categories. Through this confusion of observation and nomenclature it can be stated that energy is indeed one "thing" and the cacophony of units can be stated in one relationship.
Newton's First Law: p = mv is validated by observation and reason. What unobserved quantity maintains the objects momentum, p, and velocity, v, while being consistent with the Physics developed thus far? This unobserved quantity is a property of the object "maintaining" the velocity of the object. This is a very simplistic interpretation of the unobserved quantity, energy, and has limited usefulness. Energy, E, is hypothesised to be a scalar with the following dimensions
When the moving ice cube collided with the stationary cube it did work as measured by the change in motion of the stationary ice cube. Interestingly, the total momentum before and after a collision does not change. It is distributed between the objects. Momentum is said to be conserved property within a system that does not experience external forces. This turn out to be true for any number of colliding objects. The same concepts of conservation, interactions by forces, work, distribution of motions, and maintaining of the velocity of objects is shared by the unobserved quantity defined as energy.
[M][L][L]
-----------
[T][T]E = pv = mvv =
Defining energy with the dimensions [M][L]2/[T]2 based on an intuitive philosophical leap or an IOTTMCO guess based on algebraic manipulation and observation turned out to be a "really good guess". The most recognized equation in the World
E = mc2has the same dimensions. It is credited to Albert Einstein from his 1905 paper "Does the Inertia of a Body Depend upon its Energy-Content?" which surprisingly does not has the equation written in its famous form.
E
---
c2hν
---
c2mc2
----
hm = = <=> ν = <=> E = mc2
The important point in this Footnote is that "Energy is Energy. All the names and units used to measure it are really the same. Energy can be neither created nor destroyed, only change from one form to another". As for Einstein's Equation with Plank's Constant, h, frequency, ν, and speed of light, c, keeping mass, m, and energy, E, in proportion will require a bit more Physics to grasp.
A Comment On Refinement
Billy Pilgrim is a character in the book, "Slaughterhouse-Five" written by Kurt Vonnegut Jr., who has come unstuck in time. Comprehending Physics Equations share this quality with Billy Pilgrim. If you find a book or three by Kurt Vonnegut Jr. you will find them multi-facetted, woven with rich textured layers of storylines and plot making them all thought provoking and entertaining.
The understanding of the construction of a universe can be told in a historical chronology of discovery or built from fundamentals. However, certain fundamentals require a historical context to be made understandable. Physics is and always has been a developing science of discovery and refinement. A telling of this tale combining the chronology and the build feels reasonable. The six basis elements: existence, observation, length, time, relativity, and mass have yielded explanations for and relationships among a handful of physical phenomena. Everything stated in this paper so far is valid and consistent, but some of these thing will be found to be special cases of a more general or refined principle. It all still works and it works more completely when more is observed and understood. The need for further refinement will be addressed in the following pages to the extent that I am able. Further refinement where needed will be through the efforts of the reader. To this end I say "Thank you".
IOTTMCO Discoveries Explained
Everything is in motions. When I say something is at rest, not in motion, it underscores the bias I have that it is not moving relative to me. After all, I am the center of the Universe. This bias is acceptable because anyone can say it and determine the fundamental Laws of the Universe and be in agreement with everyone else. Newton's Three laws of Motion
Newton's First Law: p = mvEvery object will remain at rest or in uniform motion in a straight line unless compelled to change its state by the action of an external force.Newton's Second Law: F = maThe rate of change of momentum, acceleration, produced by a particular force acting on a body is directly proportional to the magnitude of the force, inversely proportional to the mass of the body and in the same direction of the particular force.Newton's Third Law: F 12 = - F 21To every action there is always opposed an equal reaction; or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts. "For every action there is an equal and opposite reaction."
communicate the the base principles between moving frames. Using algebra and calculus to combine these Three Laws render a large number of models for the Physical World. Many phenomena look and feel different but they are essential the same.
Acceleration due to Gravity, Weight, Normal Force, and Friction
When you stand on the floor you feel the Force of Gravity pulling you down. Actually, there is no "Force of Gravity". There is an Acceleration due to gravity that is retarded by the Normal Force of the object that is supporting you, but it is convenient and practical to calculate the acceleration as a force. Say, a friend drops a baseball out of a second story window. You catch it, momentarily retarding its acceleration, and then drop it. No big deal. But say your friend, drops a grand piano out the window. You do not want to repeat the experiment even though the ball and piano would have the same acceleration at the height of your hand.
Or consider, you are walking up a steep hill of about 30 degrees. You feel a resistance to each step taken which is not felt when walking on a level surface. If you slip, you accelerate downhill parallel to the grade. The perception of a force parallel to the slant of the hill and opposite to the direction you are walking is undeniable; but what is generating this force? Gravity is accelerating you straight down, vertical, and the hill is exerting a normal force to support you. The Normal Force is perpendicular to the surface of the hill and is 30 degrees less than vertical. The magnitude of the Normal Force is less than your weight, N = mg cos θ, proportional to the angle of elevation. Adding your Weight (force) and the Supporting force (Normal Force) reveals the small perceived force tugging you downhill. When you are able to stand motionless on the incline it is because the tugging force is balanced by an equal and opposite Frictional Force. A frictional force is proportional to the Normal Force, the substances in contact and their relative motion perpendicular to the Normal Force.
Static Frictional Force: F s ≤ μ sNNewtonian Mechanics provides a framework for describing the Universe defined by the Kinematics and Dynamics of a System. Where the System is a neighbourhood of the Universe that can be measured. The measurements may be made directly or indirectly depending on its scale relative to Humans and Technology. Kinematics is a complete description of the Present: Length[L], Time[T], and Mass[M] are Fundamental for now. Dynamics is the cause of change from past to present to future.
Kinetic Frictional Force: F k = μ kN
A wise man once said, "Think about Physics with a pencil". To this I would add, "Expand and contract the drawings and equations to capture the Detail and Fundamental".
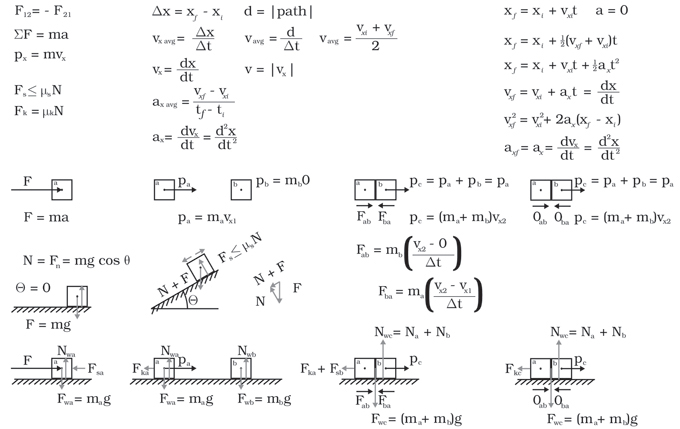
Motion and Gravity
Everything is in motion. Planets move around suns. Solar Systems orbit their neighbours, which in turn orbit the Galaxy. Clusters of galaxy dance their waltz through light years of distance. The web of galactic clusters hurtle through the Universe as far as the eye can see. Going small, the surface of the Earth is traveling about a thousand miles per hour around its core. We see objects moving all about us daily. We know about motions we cannot see and perceive them as pressure and temperature. By the "Principle of Relativity" we can pick a point and call it Zero. The chair next to the table are at rest. They have zero motion relative to each other. Many motions fade into the background and can be ignored, however Fundamentally the vast array of motions are present in the description of the System. Details ignored in the past become significant in the future when they are understood for their influence in the present.
p= mv, demands a rewrite of the first sentence of this paragraph. Motion is inherited in our world. The best fit theory of the origin of motion is the "big Bang". The transfer of motions from "stuff" to "stuff" traces back to when only Energy existed and prior to the creation of stuff.
Newton's Law of Gravity has stood the test of time for over 300 years.
m 1m 2
------
r2[L][L][L]
-----------
[M][T][T]F = G G = G = 6.67 × 10-11 m3kg-1s-2
This law provides a description of how Gravity works and has always been silent as to what Gravity is. Objects move on an inert, unchanging stage where Time "ticks" uniformly from past to future and "now" is the same everywhere. Length and Time are two separate Fundamental entities in Newton's description which are immutable everywhere and every when.
The Theory of Gravity was refined in the early 20th century by Albert Einstein to account for the motion of a relatively small mass object very close to a very large mass object. The implication was that the stage of Length and Time was not inert nor were Length and Time two separate Fundamental entities.
Einstein's Field Equations are a Piece of Cake
He developed a Notation System where one letter can stand for a set of equations. The set of equations are then consistent with the Operations defined by an equation of larger scope. Each term is more than arbitrary variables like y = f(x), though y is constrained by the value of x and x itself is constrained by the operation of f(). These steps of Constraints form a path to Concepts. Now step along a path of Concepts guided by the considerations laid down thus far, existence, observation, length, time, relativity, and mass.
Einstein's Field Equations Solutions come in various forms based on the level of detail desired and the application. Here is a form that serves as a basic comparison to Newton's Law of Gravity which is a specific case of Einstein's Field Equations for General Relativity
where G measures curvature, G is the Newtonian gravitational Constant, c is the speed of light, and T measures matter content of the system.
8πG
----
c4G = T
The terms G and T are sets of equations imbedded in G = (8πG/c4)T which if expanded would obscure the concepts of curvature and matter content. "Matter tells Spacetime how to curve, and Spacetime tells matter how to move", said John Wheeler because he saw the link between G and T and knew what G and T are.
We will start with G and build Newton's stage out of Wooden Blocks, rows and columns to make a layer and then layer upon layer to fill a space. Every rigid block has its identical rigid neighbours. The edges of the blocks make up a rigid coordinate system identifying up-down, right-left, and forward-backward. No matter where you are Time "ticks" simultaneously and uniformly from past to future. If you are here and someone is over there, then something happens elsewhere. Everyone in Newtonian Space and Time agree when and where "it" happens. Observations revealed details that show Newton's Law of Gravity is a special case solution of the large scope description of gravity encapsulated by Einstein's Field Equations.
Replace the Wooden Blocks by soft stretchy spongy cubes. Each cube continues to "tick" Time from past to future. Each tick is the amount of Time it takes for light to traverse an edge from corner to corner. This "time scale" applied to Newton's Blocks by Einstein comes from Maxwell's Equations. There is much to be said about Maxwell's Equations, but for now all we need is the maximum "Speed of Light", c. The block can now be squished, stretched, twisted, dimpled, bumped, curved, concaved, convexed, and even flattened to resemble rigid Wooden Blocks. When a volume is compressed the lines of spacetime (space and time) get closer to each other, When stretched they diverge to increase the distance between events in space and time (spacetime).
In our everyday world we experience the lines of spacetime as parallel and evenly spaced. We each live on our own line of spacetime. If I agree to met you at Joe's Market a 3 o'clock and we both arrive on time our spacetime lines have converged. After picking up our Lottery Winnings we leave to go our separate ways, our spacetime lines have diverged. The distance of our spacetime paths we traveled to and from Joe's Market are determined by the soft stretchy spongy cubes of spacetime that envelope our Neighbourhood. The spacetime cubes are so close to the Newtonian Wooden Blocks that we get the same results we calculating the distances traveled and the time spent to pick up our Lottery Winnings. Truth be told, Newton's Wooden Blocks work for describing the orbit of the Moon and the Planets around the Sun. Except for a small detail about Mercury's Orbit.
The Wooden Blocks of Newton were somewhat squish and twisted. What's more, time played into the proper squish and twist of the Blocks so they could be dynamic enough to work at Joe's Market, the Moon and the orbit of the other Planets. The un-parallel-ness and un-evenly spaced lines of spacetime in the Neighbourhood of the Sun cause Mercury to fall in the observed orbit it has around the Sun.
So, "Spacetime tells matter how to move" is the G part of Einstein's Field Equation. "Lets have some Cake".
You come home one day and smell someone has been baking. A 9 by 13 inch White Cake is near. The aroma is intoxicating. Upon entering the kitchen a golden cake with just the hint of chocolate swirls on top meets your gaze. "No frosting, the deliciousness is in the Details", the Master-Baker slices a piece of Cake. A dense Brownie Mix had been swirled in to the lighter White Cake Batter. You can not fathom how they could have baked together. But, I digress. The textures delight your Taste. There is something else, robust and tantalisingly gooey. Yes, it's peanut butter but there is more. Small, sharp, hard, well defined. "My God, its full of heath toffee."
And that's what matter content T is, the ingredients keeping their distance one from another by their nature (mass and a few more) yet influencing the baking in the distance between (spacetime).
Paths not Taken
Here are things which fascinate me and slip from my grasp. My understanding of them is not deep nor wide enough to explain them to myself or in explaining one I lose my understanding of the world. These are the concepts in my realm of contemplation. I accept their shadows as guideposts to Understanding. The shadows are tools I humbly use to explain what I can, yet I am justified in do this by a Powerful Mathematical Theorem
The IOTTMCO Theorem ≡ Intuitively obvious to the most casual observer
The Mathematical Reasoning used to define the cosine function results in the Taylor serie
The Mathematical Reasoning used to define the sine function results in the Taylor serie
x2
---
2!x4
---
4!x6
---
6!cos x = 1 - + - + ⋅⋅⋅
∞
Σ
n = 0(-1)nx2n
----------
(2n)!cos x =
Linear Algebra provides many mathematical tools used in Physics.
x3
---
3!x5
---
5!x7
---
7!sin x = x - + - + ⋅⋅⋅
∞
Σ
n = 0(-1)nx2n + 1
----------
(2n + 1)!sin x =
The number π is a Fundamental Relationship.