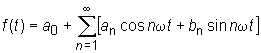
FOURIER SERIES

Any periodic function f(t) with period T can be presented as a sum of sines and cosines of argument nwt, where n is an integer number, t is time, w =2p/T (so called Fourier series):

where          


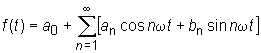
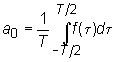
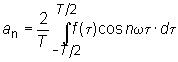
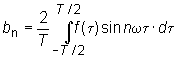
Fourier components of this series are called as harmonics. Any even function is expanded in a series of cosines and any odd function is expanded in a series of sines. In some cases the even harmonics are absent.

 

 

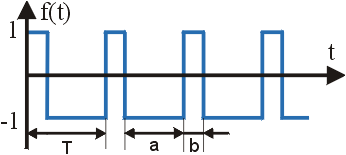
1. Let us consider meander with angular frequency w as it is shown in the figure (where a=b=T/2). This function is expanded in a series:

Animation below shows sum of the first 10 harmonics of Fourier composition of meander. We can see from this animation that first harmonic component is a sinus. Adding the higher harmonics we distort this sinus and, finally, the sum of first ten harmonics (the highest of which is of the frequency 19w ) gives the practically ideal meander.

2. Let us consider the other example of the function shown in the figure where T/b=4. This function can be expanded in Fourier series as follows:

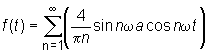
image92.gif

Animations below shows the sum of the first 20 harmonics of the Fourier series. We can see in this figure that the function is mainly built by the first several harmonics. The high-order harmonics improve the sharpness of the fronts.

impuls