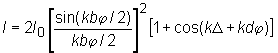
where I0 is the intensity of the light in the center of diffraction
pattern when only one slit is opened, b is the width of the slit, d is
the distance between the slits, k=2p /l is the wave factor, l is the
wavelength, D is the difference of the optical lengths of
the interfering rays (in the case, for example, when the wave is incident not
perpendicularly to the screen or one slit is covered by glass). The first multiplier of
the equation in the square brackets describes the Fraunhofer diffraction on one slit and
the second multiplier describes the interference from two point sources. The total energy
of the light getting through the slit is proportional to b, while the width of
the diffraction pattern is proportional to 1/b. For this reason the intensity of
the light I0 in the center of diffraction pattern will be proportional
to b2. In the limits of the first diffraction maximum we can see N
interference fringes, where N=2d/b.
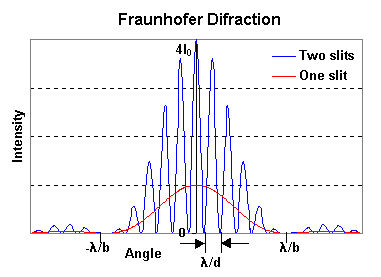 This figure shows the dependence of the light
intensity on the angle in the case of diffraction on one slit (red curve) and for two
slits diffraction (blue curve). We can see in this figure that the maximal intensities of
the interference fringes follow the curve for diffraction on one slit.
This figure shows the dependence of the light
intensity on the angle in the case of diffraction on one slit (red curve) and for two
slits diffraction (blue curve). We can see in this figure that the maximal intensities of
the interference fringes follow the curve for diffraction on one slit.
Talking about "Fraunhofer" diffraction we mean the far-field diffraction,
i.e. when the point of observation is far enough from the screen with the slits.
Quantitatively the criteria of the Fraunhofer diffraction is described by the formula:
z >> d2/l
where z is the distance from the screen with the slits to the point of
observation. In the close proximity to the screen with the slits the diffraction pattern
will be described by the Fresnel's equations.
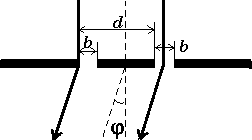 Let us consider the screen with two slits
illuminated by a flat monochromatic wave. Calculations show that the intensity of the
light getting pass through the slits will depend upon the angle j
between the direction of the light propagation and the perpendicular to screen:
Let us consider the screen with two slits
illuminated by a flat monochromatic wave. Calculations show that the intensity of the
light getting pass through the slits will depend upon the angle j
between the direction of the light propagation and the perpendicular to screen: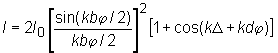
 This figure shows the dependence of the light
intensity on the angle in the case of diffraction on one slit (red curve) and for two
slits diffraction (blue curve). We can see in this figure that the maximal intensities of
the interference fringes follow the curve for diffraction on one slit.
This figure shows the dependence of the light
intensity on the angle in the case of diffraction on one slit (red curve) and for two
slits diffraction (blue curve). We can see in this figure that the maximal intensities of
the interference fringes follow the curve for diffraction on one slit.

