Plots of one joint angle against the simultaneous value of another joint angle give insight into intersegmental coordination.  Here are some common interpretations: 

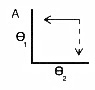
Horizontal and vertically aligned segments indicate a decoupled coordination, with one joint angle changing very little relative to the other (Figure 1A). 

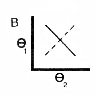
If a trajectory segment is a diagonally oriented straight line, the two angles are changing at a constant ratio (Figure 1B). 

- if this straight line segment has positive slope, the joint angles are moving in phase (flexion in one with flexion in the other) 

-if this segment has negative slope, the joint angles are moving out of phase (flexion in one with extension in the other)

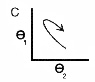
Another important feature of these plots is termed turning point synchronization, in which two joint angles reverse direction nearly simultaneously (Figure 1C). 

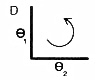
In contrast, segments with large curvature correspond to epochs in which there is significant alteration in the relative rates of change of the two joint angles (Figure 1D). 
 
 

SHAPE	DESCRIPTION	INTERPRETATION
	Horizontal or vertical segments	One joint angle changing while the other is held constant
	Diagonally oriented straight line with negative (positive) slope	Two joint angles coordinated out of phase (in phase); changing at a constant ratio
	Both joints reach their maxima and switch simultaneously	Turning point synchronization; intersegmental coordination at switching point
	Rounded trajectory	Phase offset; decoupled coordination

Figure 1.  Selected shapes of trajectory segments in angle-angle space with dynamical interpretations.  Adapted from Winstein and Garfinkel (1989). 
 
 

top

  

Melissa Gross , Ph.D. - mgross@umich.edu
The University of Michigan, Division of Kinesiology

Revised 9/99
©1996 Melissa Gross, Ph.D.