UofM NERS/BIOE 580 - 10_Image

NERS/BIOE 580
Lab10 - Image Module B

Purpose:

In the previous module we examined the contrast to noise ratio ( CNR ) associated with a small target object embedded within the tissue structure being radiographed. The kVp that optimizes the CNR in relation to the subject exposure was determined for both chest imaging and mammography.
Computed tomography uses radiation transmission measurements made at many positions and angles to deduce the interior material properties of the object. The measured data has noise and contrast similar to that of a radiograph. When reconstructed, this leads to noise and contrast in the reconstructed tomogram. In this lab, we will learn how the noise in the acquired projection data propogates to noise in the reconstructed tomogram and will evaluate the CNR of a reconstructed tomogram in related to subject exposure.

Discussion:

For x-ray computed tomography (CT), the material property determined is the linear attenuation coefficient. When using a broad spectrum of radiation to make the transmission measurements, this is the effective linear attenuation coefficient, µ_eff, that we determined as a part of the prior lab module (Lab09). For medical devices, this is normalized by the µ_eff of water and expressed as the Hounsfield Unit ( HU ):
HU = 1000 * [ ( µ_obj^eff - µ_H₂O^eff ) / µ_H₂O^eff ]
HU = 1000 * ( µ_obj^eff / µ_H₂O^eff ) - 1000

Thus 1 HU is a 0.1% change in the attenuation coefficent and the scale is offset such that water has HU = 0. To analyze CT signal characteristics, we will use in this lab a modified unit of HU' = HU + 1000 which is 0 for a vacuum and increases linearly with the effective attenuation value.
The signal difference between HU' for a small target region, HU'_t, and for surrounding background regions, HU'_b, divided by HU'_b is the relative contrast, C_r. The CNR is the product of C_r and the CT signal to noise ratio, SNR_CT, determined using the noise in the background region of the reconstructed CT image;

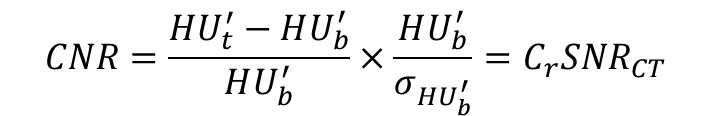
where σ_{HU'_b} is the standard deviation of the noise in the reconstructed image.

Based on the definition of HU', it is easy to see that;

and;

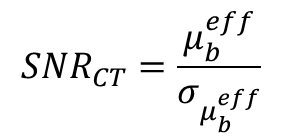
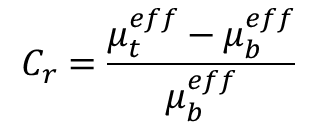
For CT, the SNR and relative contrast, Cr , are thus seen to be analogous to the definitions used for radiography. For SNR , the CT expression reflects estimates of µ_eff wheras the radiographic expression reflect the measured detector signal. The radiographic relative contrast for a small target is given by Δ µ_eff times the object thickness wheras the CT expression is the relative change in µ_eff . CNR for a CT system can thus be evaluated using scripts similar to those used for radiographic systems.
The projection measurements made by a CT scanner derive from detector signals that are the same as those recorded by a radiographic detector. The projection values correspond to the line integral of the linear attentuation coefficient along various paths through the object and are deduced from the natural log of the ratio of the detected signal with and without the object. As such, the noise for the CT projection values, σ_p , can be shown to equal the relative noise associated with the detected signal, i.e. 1/SNR_p.
The noise in the measured projections propagates through the image reconstruction algorithm to produce the noise in the reconstruction. From an analysis of the propogation of noise for a filtered backprojection algorithm under the assumption that the reconstructed pixel size is matched to the spacing of the detector elements, it can be show that;
σ_ct = σ_p / ( 2.0^1.5 δ N_v^1/2 )
where δ is the size of the reconstructed pixels and N_v is the number of projection views. The derivation assumes a parallel projection beam, but is applicable to a fan projection beam for targets near the center of the object. The constants in this term are specific for a reconstruction done with a sinc filter function. Further information on the derivation of this expression can be found in ctNoise_v4.pdf

Task Img-B1: Computation of SNR_ct from radiographic SNR.

The extension of a radiographic CNR analysis to a CT analysis is facilitated by the fact that SNR_ct is linearly related to the SNR associated with radiographic signals. The equations above can be rearranged to give;
SNR_ct = µ_eff ( 2.0^1.5 δ N_v^1/2 ) SNR_p

A utility program is availabe to evaluate SNR_ct from it's independant variables. A description of this program, ct_snr.txt , is in the documentation directory. The tcl procedure to call this program has 5 arguements;
ctSNR {deltaCT Mu_bgd SNR viewsCT prtFlag}
Read the documentation before starting the following task.

Task Img-B2: Model for CNR in patient vascular CT.

As a part of Lab09, you were asked to save the script model associated with the evaluation of radiographic CNR for an ideal detector and a 14 cm thick object (12cm tissue and 2cm fat, 40 to 250 kVp). This model used a tungsten target x-ray source with intrinsic filtration consisting of .24cm glass-pyrex, .31cm oil, .27cm lexan (GE Maxiray 125). We will use this for all tasks in this lab. However, the added filtration which was 0.15 cm of al_1100 will be changed.
Begin by renaming the saved script and changing the model identification in the header to describe the CNR analysis of a computed tomography system. If the script from Lab09 had the model parameters nicely collected at the beginning, most of the modifications needed for this module will be simple to make. If not, take a few minutes to collect the model parameters to facilitate the model changes needed in the next section. The table at the end of this module can be used as a guide for parameter names and values for the various input variables that need to be defined. For this task we will use the column for 'patient CT'. The values of computed parameters are listed at the bottom of the table.
Next the parameter definition need to be change in a manner consistent with the equations above in the Discussion section. For the previous radiographic model, the target contrast was determined from the altered transmission through a target with specified thickness. For the CT problem, the target contrast is determined from the change in the attenuation coefficient for the target in relation to the surrounding tissue. The CT target has a specified diameter but no thickness since the reconstruction is done in a two dimensional plane.
Make the following modifications to the general radiography CNR script in the section where parameter values are assigned.

*NOTE: The capital labels below, OBJ:,TAR:,..., refer to the parameters shown in the table at the end of this module. The items with an * are computed values.

Change the previously defined parameters as described below:

OBJ: Change the muscle thickness to 15 cm,
add a bone2.2 thickness of 1.0 cm,
and leave the fat tissue at 2 cm
for a total object thickness of 18 cm.
TAR: Change the target background material to muscle
and the target material to bone2.2.
TAR: Change the target diameter (i.e. thickness) to 0.1 cm.
*TAR: Compute the target area as the area
of a circle with the above diameter.
DET: Change the detector to 'ideal.det'.
DET: Change the detector element size to 0.04 cm.
*DET: Compute the detector element area,
as the square of the above element size
(i.e. detector elements of .4 mm by .4 mm)
GEOM: Change the detector distance to 120 cm.
GEOM: Add a variable for the distance to the object center
and set it to 90 cm.
(This is the CT rotation center)

*GEOM: Compute the distance to the front of the object such that
it is centered at a distance of 90 cm.
(i.e. 90 - (15 + 1 + 2)/2 = 81)

RAD: Change the added filtration to 0.10 cm of al_1100.
RAD: Reduce the mas per projection to 0.5, and

Add new parameter values for the number of CT views and the spacing of values in the CT reconstruction. The CT reconstruction spacing should be computed by reducing the detector element size, deltaCT, by the magnification. (i.e. detSize * (objCtrDist / detDist) )

CT: set viewsCT 720
*CT: compute deltaCT

The object size and composition is similar to the head, neck or thigh of a person. The target is typical of the cortical bone in the femur or a vertebra. The ma-S specified is for each of the 720 views. For a device that completes the 720 views in 1 second, this requires 360 mA average current for the x-ray tube. The value computed for the reconstruction spacing, deltaCT, will be .030 cm (i.e.the detector size of .040 cm when scaled to the object center to account for the use of a fan beam projection). Since medical CT detectors have very high detector efficiencies, the use of an ideal detector is a reasonable approximation. In the next section, this will be changed to an actual detector of the type that is used for cone beam tomography.
In the body of the prior script, inside the loop over kVp, make the following changes;

In the prior script, detect (detect.tsp) was used to evaluate the noise equivalent quanta, NEQ, which is understood to be SNR_p². Immediately following this section, add a procedure call for ct_snr (ctSNR .....) and use the square root of NEQ as the input SNR_p. Otherwise input the deltaCT and viewsCT values defined above along with the effective linear attenuation coefficient, mu_eff, for muscle which was previously computed.
For this model, we will need to know the effective attenuation coefficient for water, fat and muscle. In the section where mu_eff is evaluated, add calls to mu_eff to determine these values and assign them to named variables.
Change the expression for the relative contrast, Cr, such that Cr is equal to the difference between the mu_eff computed for the target material and the background material divided by the mu_eff for the background material.
i.e. (µ_bone^eff -µ_musc^eff) /µ_musc^eff)
Revise the final expression for CNR to reflect the desired CT result of Cr * SNR_ct and change the results written to a file and used for plots.
Specifically report;

CT CNR adjusted for the target area,
Average exposure from all views in R,
mR_avg = (mR_input + mR_exit)/2 (i.e. average mR per view)
R_avg = (mR_avg/1000.0) x viewsCT (i.e. average R, all views)
Dose normalized CNR,
i.e. CNR / SQRT(R_avg)
Optionally report mu_eff values for muscle, fat, and bone, and
Optionally report projection NEQ and SNR_ct.
For CNR, the results computed for each pixel needs to be adjusted for the target area as was done in the prior lab. In this case, the target needs be adjusted using the reconstruction spacing, deltaCT, which is the pixel size of the CT image,
... [expr $CNR*sqrt($targA/($deltaCT*$deltaCT))]
For the exposure, the result computed for each projection view should be multiplied by the number of views to get the total average exposure.
Finally modify the loop around the body of the script to compute values every 2 kVp from 40 to 160 kVp.

Run the script and plot the CNR normalized by the square root of the average exposure. From the output data, identify the kVp producing the maximum value for the exposure normalized CNR (i.e. CNR/sqrt(exposure). A maximum of 52 should be found at 120 kVp when the exposure is expressed in Roentgen units (i.e. R as opposed to mR as was done in Lab09). For human subject imaging, 120 kVp is commonly used.

Task Img-B3: Models for small object CT.

For this final task, we will just change the model parameters to determine the optimal kVp for two CT systems used to examine small objects. To make this easier, move the the model parameters collected at the beginning of your script to a text file with a name such as Params-patientCT.txt. Then insert a command to source these parameter definitions;
source Params-patientCT.txt
Then make two copies of this file named Params-animalCT and Params-specimenCT and change the parameter values to those in the two right columns of the table below. Note that the minimum, maximum, and increment for the kV loop are defined as parameters and need to be changed. The new models can now be run simply by changing the file sourced to set the parameter values
The detector used for both of these models is a Selenium direct digital radiography panel, SeTFT-lorad.det, capable of rapid sequence acquisitions. This type of detector is often used in cone beam CT systems where the detector and x-ray source rotate about the object in a circular orbit. The geometries for these two models involve more magnification than was used in the model studied above. With a smaller detector element size, 0.1 mm x 0.1 mm, and with the higher magnification, the reconstruction pixel size is much smaller.
The 'animal CT' system is typical of devices used to examine mice and rats in medical research facilities. The object size is 8 cm and the geometry uses a magnification of 100/70. A tungsten target x-ray source that is similar to the first model studied above is used. The target size is set to represents the cortical bone found in in the skeleton of these small animals. The maximum dose normalized CNR of about 50 occurs near 38 kVp.
The 'specimenCT' system is typical of devices used to examine tissue specimens. The object size is set at 1.2 cm and the geometry uses a magnification of 100/20. The bone target for this model has a size similar to the trabecular structures in cancellous bone (i.e. spongy bone) for which the bone marrow material is similar to fat. Specimens of this type are obtained from the iliac crest at the side of the hip using a biopsy tool. Since we expect a lower kVp due to the small size of the object, the added filtration should be changed to 0.0050cm of tin (i.e. tinpure). The maximum dose normalized CNR of about 17 occurs at near 28 kVp. Note that higher kVp values can be used with little penalty.

- patient CT - - animal CT - - specimenCT -

OBJ: muscle thickness,cm muscleT = 15.0 7.0 0.0

OBJ: fat thickness,cm fatT = 2.0 1.0 1.0

OBJ: bone thickness,cm boneT = 1.0 0.0 0.2

TAR: target material target = bone2.2 bone2.2 bone2.2

TAR: background material backgd = muscleNBS muscleNBS fatNBS

TAR: target diameter,cm targT = 0.1 0.050 0.015

DET: detector file name detector = ideal.det SeTFT-lorad.det SeTFT-lorad.det

DET: det. element size,cm pSize = 0.04 0.01 0.01

GEOM: dist. to object ctr. dist1 = 90.0 70.0 20.0

GEOM: dist. to detector,cm dist2 = 120.0 100.0 100.0

CT: number of proj. views viewsCT = 720.0 720.0 720.0

RAD: ma-S per proj. view mas = 0.50 0.50 0.50

RAD: added filter material filter = al_1100 al_1100 tinpure

RAD: filter thickness,cm filterT = 0.10 0.10 0.0050

SRC: Anode atomic No. anode = 74 74 74

SRC: Anode takeoff angle angle = 10 10 10

SRC: Spectrum energy incr. incr = 1.0 0.5 0.5

ITR: kVp minimum minKV = 40.0 20.0 20.0

ITR: kVp maximum maxKV = 160.0 80.0 50.0

ITR: kVp increment kvincr = 2.0 2.0 1.0

*OBJ: Object thickness,cm tissueT = 18.0 8.0 1.2

*TAR: Target area,cm2 targA = 0.00785 .00196 0.00018

*DET: det. element area,cm pArea = 0.0016 0.0001 0.0001

*GEOM: dist to object,cm dist0 = 81.0 66.0 19.4

*CT: recon. pixel size,cm deltaCT = 0.030 0.0070 0.0020

* Total object thickness from muscle, fat, and bone thicknesses
* Target area computed as area of a circle with the target diameter
* Detector element area computed from element size
* Detector distance to object surface is the object center distance less 1/2 the object thickness
* reconstruction spacing computed from detector size and magnification (dist2/dist1)

Lab10 Results:

For this module, turn in the final script and the plots for normalized CNR showing the optimal kVp for the three scenarios (patient CT, animal CT, and specimen CT).

L10-Img-B2.png : Dose normalized CNR vs kVp, patient CT.
L10-Img-B3_1.png : Dose normalized CNR vs kVp, animal CT.
L10-Img-B3_2.png : Dose normalized CNR vs kVp, specimen CT.
L10-Img-B3.tcl : final script for Lab10.

L10-Img-B3 Reference script: Lab10_Img-B3.tcl

Note: this reference script includes a tk window in which the model type is first selected;

patient CT
small animal CT
specimen CT

and then a second window presents the default variable values in entry widgets which can be used to make parameter changes. Rather than sourcing the parameter values from text files, they are set at the beginning of the script as three groups for each of the model types. An if {...} elseif {...} elseif {...} structure is used to set the selected parameters.

NERS/BIOE 580 Lab10 - Image Module B

NERS/BIOE 580
Lab10 - Image Module B