J.F. Wambaugh¹, F. Marchesoni^1,2, and Franco Nori^1*
    1. Department of Physics, University of Michigan, Ann Arbor, Michigan 48109-1120
    2. Istituto Nazionale di Fisica della Materia, Universit'a di Camerino, Camerino, I-62032, Italy

We study via computer simulations the motion of magnetic flux-line vortices (fluxons) confined to a straight pin-free channel in a strong-pinning superconducting sample.  We find that, when a constant current is applied across this system, a very unusual oscillatory shearing manifests, in which the fluxons at the edges of the channel repeatedly trail behind and then suddenly leapfrog past the inner rows.  For small enough driving forces, the oscillatory shearing dynamic phase is replaced by a continuous shearing phase in which the distance between initially-nearby fluxons grows in time, quickly destroying the order of the lattice.
 

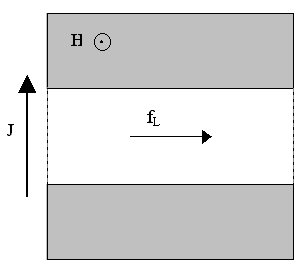Simulation --- Unless otherwise specified, each figure refers to simulations conducted in the following way:  Initially fluxons were placed uniformly across the sample in a minimum-energy, field-cooled triangular lattice and the fluxons in the channel were subjected to a current along y; producing a Lorentz driving force F º f_L / f₀ = 15.  The square sample had side 18 l and the central straight channel was parallel to the x-axis, centered in the sample and 7 l wide.  This configuration is schematically depicted in Fig. 1.  The initial triangular distribution resulted in roughly two thirds of the fluxons being fixed in the very strong pinning region outside the central channel.  The square sample had periodic boundary conditions, allowing free fluxons in the channel to continue moving along the x-axis indefinitely.  Because of the channel walls, periodic boundary conditions along the y-axis did not affect the dynamics.  Typically Dt = .01 was used. giving the unit of time t = 100 MD steps.





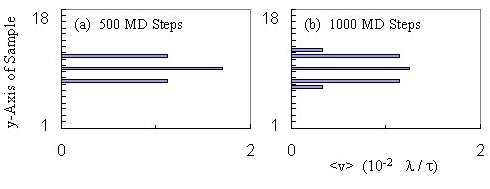
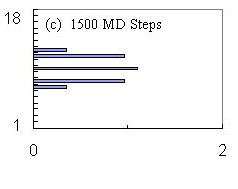
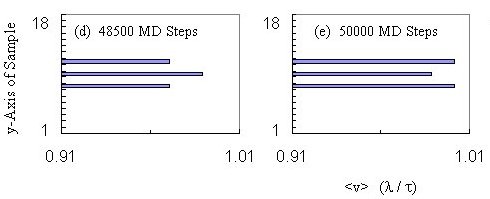
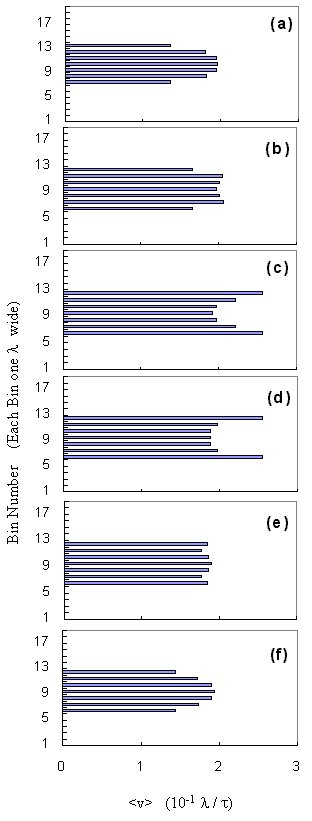
Fluxon Velocities inside the Channel --- Figure 2 shows a "velocity profile" computed by dividing the sample into 1 l wide, horizontal "bins" and averaging the velocity of those fluxons in each bin.

We want to monitor the time evolution of v(y), since shear implies a non-zero gradient along y of v(y).  We have found that binned velocity snapshots, like the ones shown in Fig. 2, are useful because they illustrate the shear-induced presence of gradients in v(y).  Thus, we binned the fluxon velocity along y and integrated the velocities along x.

The two sequences [(a--c) and (d--f) in Fig.~2] of velocity profiles across a channel are successive velocity snapshots.  These snapshots are made every 500 MD steps during the course of a simulation: (a--c) shows three successive snapshots, while in (e--f) every third snapshot is shown. These two particular chronological sequences show two different types of behaviors that we have found when a perfect triangular lattice of fluxons is placed and then forced to move on a superconducting sample with a straight channel.

Continously Sheared Dynamic Phase for Low Driving

Sequence (a--c) in Fig. 2 corresponds to a relatively weak driving force of magnitude F = 0.02, and displays the expected "beer-belly" curved velocity profile.  Here the shear between the edge fluxons of the channel and the pinned fluxons outside the channel induces a curvature in the velocity profile.  In (a), the edge rows, interacting with the infinitely pinned fluxons experience drag, resulting in the inner row moving slightly faster.  The interaction between the inner (bin 9) and outer (bins 7 and 11) fluxon rows pulls the outer rows along, eventually pushing outwards a few fluxons in the edge rows---as they catch on the pinned fluxon potential, as shown in (b).  This outward displacement of a few edge fluxons creates defects in the moving fluxon lattice and also the appearance, in the velocity profile in (b), of moving fluxons (in bins 6 and 12) where there were previously none.  For this low density of fluxons, and for our chosen fine-grained bins, there are no fluxons in bins 8 and 10.  A higher density example will be discussed below.  In (c), the velocity profile has remained "fanned out" as the fluxons continue to be driven.  The original triangular lattice arrangement has not been preserved because the fluxon lattice has been continuously sheared, producing many defects.  Indeed, the distance between initially nearby fluxons grows with time, for low driving forces.

Oscillatory Shearing Dynamic Phase for Higher Driving

At a higher driving force, however, a novel dynamic fluxon phase is observed.  Sequence (d--f) in Fig. 2 has the same number of fluxons as in (a--c), but driven by a higher driving force; F = 1 instead of F = 0.02.  Now, instead of allowing fluxons to slip from the outer rows as they catch on the interactions with pinned fluxons, the outer rows of fluxons actually leapfrog forward past the inner row, by temporarily moving more rapidly than the inner row.  Here, (e) clearly shows the outer rows actually move faster than the inner rows.  Eventually, the faster edge rows slow down and, as shown in (f), this results in a brief effective uniform velocity across the channel.

This unexpected cycle repeats periodically and it is even more pronounced when there are higher fluxon densities, corresponding to higher magnetic fields.  The three-row arrangement shown here is just the simplest example that illustrates this novel fluxon dynamic phase.

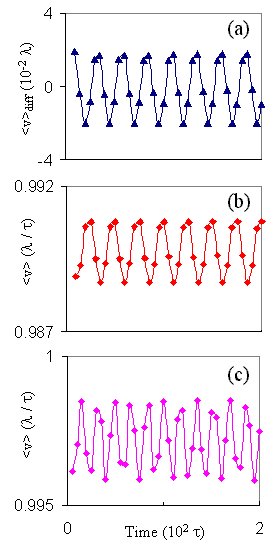Further Characterization --- Figure 3 shows the temporal evolution of the difference in velocities v_diff between the inner and outer rows (a).  The overall average velocity in the channel has also been plotted, in (b) to show how v_diff correlates to v.  The velocity in (b) changes to (c) when the number of vortices is increased from 80 to 340.  Below is a contour giving the evolution of velocity across the channel with time.

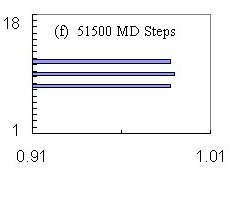
Leapfrogging Edge Fluxons at Higher Fluxon Densities --- The very unusual cycle of "trail-behind" and leapfrogging edge fluxons seen in Fig. 2 very clearly persists at much higher  field strengths, as indicated in Fig. 4.  There, the density of fluxons is about four times higher than in the case shown in Fig. 2.

The chronological sequence of "snapshots" in velocity space in Fig. 4 depicts the time evolution of the velocity of fluxons across the channel.  This situation is similar to Fig. 2 (d--f), but now there is a much higher field strength: 340 fluxons have now been placed in a triangular lattice on the sample with a straight central channel.  This combination of field strength and channel width results in the channel being filled with seven horizontal rows of seventeen fluxons each.

The behavior exhibited in Fig. 4 is the result of inner rows of fluxons being locked together with the outer rows despite the interactions of the outer rows with the pinned fluxons outside the zero-pinning channel.  Intuitively one would expect that profiles like (a), (b) and (f) are the norm---the outer rows snag on the pinned fluxons and lag behind the less restricted inner rows.  The surprising behavior is that profiles like (c) and (d) indicate that the slowed fluxons in the outer rows suddenly "catch up" or leapfrog by momentarily exceeding the velocity of fluxons in the inner rows.  Panel (e) in Fig. 4 shows that this can also result in a much flatter velocity profile than otherwise expected, albeit just briefly.

Simulations at both field strengths discussed here (80 and 340 fluxons on the sample) demonstrate continuous shearing under low driving forces, but unusual oscillatory shearing under higher driving forces.  In addition to higher field strengths, simulations with smaller Dt's were used, producing the same results (e.g., 0.001 instead of 0.01).  The animation shows the change in velocity profile during a simulation with smaller Dt (the velocities are larger than those in the snapshots because the particular simulation animated was conducted with F = 1 instead of F = .2 as in the snapshots).



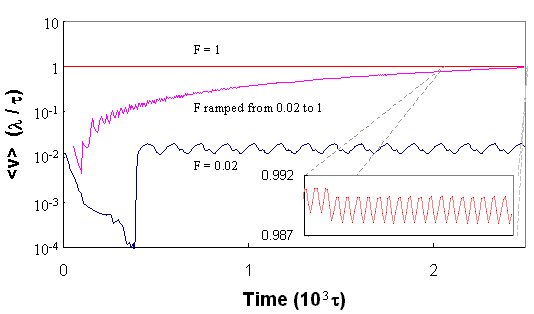Velocity versus Time for Several Driving Forces --- Figure 5 shows the fluxon velocity, now averaged over the entire sample, for the oscillating shearing phase (top curve, F = 1), the continuous shearing phase (bottom curve, F = 0.02), and an intermediate ``ramped driving" case, where the driving force is slowly increased to monitor the crossover (not a sharp dynamic phase transition) between these two dynamic phases.  Several simulations were done, but only three representative ones are shown here.

The lowest curve shown in Fig. 5 corresponds to a weak-driving case; here with force F = 0.02.  First, there is a transient.  Afterwards, the average velocity of the entire lattice, not just the edge fluxons anymore, shows marked oscillations with time.  This corresponds to a "stick-slip"-type motion of the fluxon lattice impinging upon a succession of potential energy bottlenecks as it is pushed through the channel.  Notice that strictly speaking, the "stick" phase is really moving, and never stuck.  Thus, it is more appropriate to describe it as a phase with an oscillating sine-like average velocity.  Notice also that the velocity oscillations in this low-driving "continuous shearing" dynamic phase span about 1/3 of an order of magnitude (the vertical axis has a logarithmic scale).

The highest curve in Fig. 5 shows a typical large-driving, F = 1, case.  There, the system is in the oscillating shearing dynamic phase, and the average velocity of the entire system oscillates, as shown in the magnification of this plot located in the lower right inset.  The average velocity appears to be constant in the main panel of Fig. 5 because its vertical axis spans five decades!

To monitor the crossover between these two dynamic phases, Fig. 5 also shows an intermediate curve, where the driving force was slowly increased from an initial value of  F = 0.02 to a final value of F = 1.  While the average velocity oscillations of the continuous shearing phase, the low-driving-force-regime, initially persist, it is clear that the amplitude of the velocity oscillations decrease until there is no discernable oscillation (without magnification) in the logarithmic plot.

In other words, when the average velocity of the moving fluxons is plotted over time, while the driving force is slowly increased, the average velocity eventually becomes relatively stable, in the sense that there is not much overall relative shifting in the lattice.  Thus, the lattice, while sheared with oscillating velocities,
is not completely torn apart at higher driving forces---because of the periodic "leapfrog" jumps of the trailing edge fluxons.

For the measurements shown in Fig. 5, the average displacement of all moving fluxons was recorded every 500 MD steps, over the course of 250,000 MD step simulations.  We also studied many more values for the driving force, including very high values.  For all cases where F was approximately larger than 0.05, oscillating shearing was found.

Since the oscillations in the average velocity are caused by the interaction between the moving and pinned fluxons, we have found that the frequency of the oscillations depends on the density of the fluxons (they are inversely proportional).  Thus, careful measurements of the average velocity (e.g., as a voltage), might provide an indirect way of determining the fluxon density and magnetic field strength.  Indeed, in Fig. 3, the system that produces the signal (c) is the same one as in (b) but with about four times the number of vortices.  Notice how the period decreases.
 

* Corresponding author.