Five Videos of River-Like Vortex Motion

• At very low pinning strengths, vortices flow throughout the sample in channels that braid together.
• At moderately low pinning strengths, the channels become more well defined, but still braid significantly.
• At moderately high pinning strengths, the width of the channels begins to collapse, and the amount of braiding in the channels decreases.
• At high pinning strengths, the main channels are very well defined and isolated, with little braiding.
• Quicktime movies of river-like vortex motion (Science, 1996).

Topological Invariants in Microscopic Transport on Rough Landscapes: Morphology, Hierarchical Structure, and Horton Analysis of River-like Networks of Vortices.

A.P. Mehta, C. Reichhardt, C.J. Olson, and Franco Nori,
Physical Review Letters 82 , 3641 (1999).

PS file (with no figures) of the paper is available here, while a DVI file (also with no figures) is available here

River basins as diverse as the Nile, the Amazon, and the Mississippi satisfy certain topological invariants known as Horton's Laws. Do these macroscopic (up to 10^3 km) laws extend to the micron scale? Through realistic simulations, we analyze the morphology and statistical properties of networks of vortex flow in flux-gradient-driven superconductors. We derive a phase diagram of the different microscopic network morphologies, including one in which Horton's laws of length and stream number are obeyed---even though these networks are about 10^9 times smaller than geophysical river basins.

Postcript Figures are available here:

• Fig. 1: Snaphots of northbound vortex pathways.
  
• Fig. 2: Vortex River Network Morphological Phase Diagram.
  
• Fig. 3: Pin Occupancy, Length Ratio, Fractal Dimension for vortex pathways.
• Fig. 4: The number of streams and their lengths for vortex river networks.

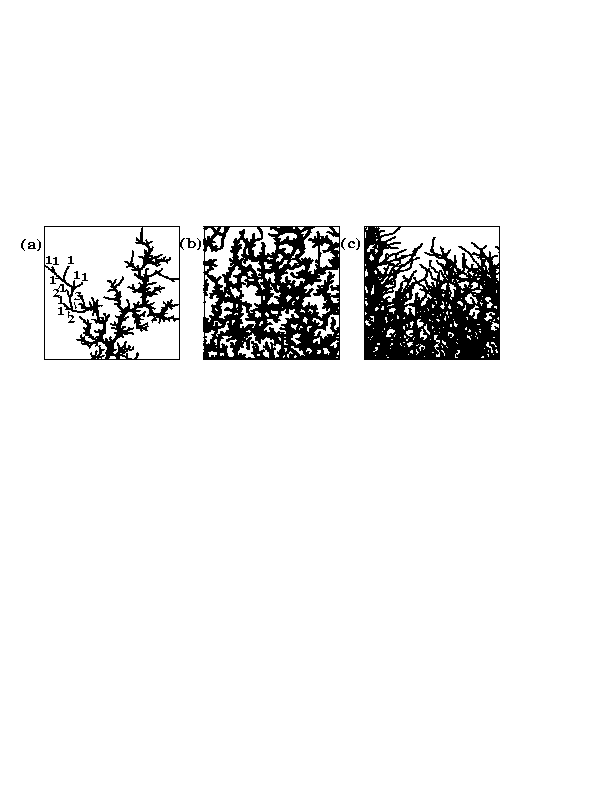
Snapshots of northbound vortex pathways: (a) Hortonian (when the pinning force, f_p, is stronger than the vortex-vortex repulsion f^{vv} ; i.e., at low B and high f_p); (b) braided (when f_p is comparable to f^{vv}: B \approx 3 B_{\phi} / 2 ); and (c) dense (when pinning is much weaker than f^{vv}; i.e., for B > 2 B_{\phi}, or at any field for low f_p). Here, n_p = 0.75 / \lambda^2. Here (a) shows a (low local B) flux-front region and (b) shows an intermediate-B section of the same sample.

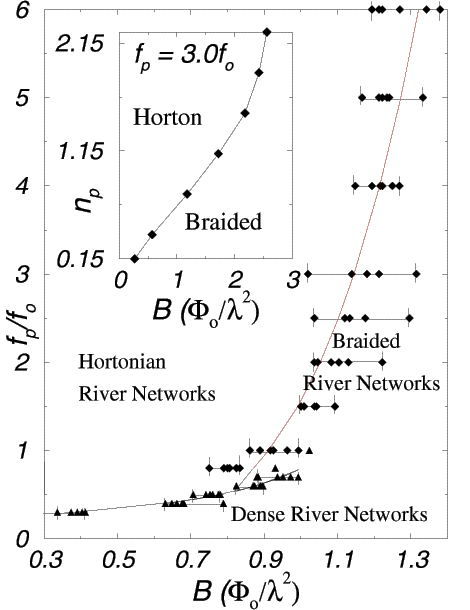
The vortex river network morphological phase diagram for pinning force, f_p, versus magnetic field, B, for n_p=0.75 / \lambda^2 (thus, here B_{\phi} = 0.75 \Phi_0 / \lambda^2). In regions of very low pinning force f_p, dense (space-filling for t \rightarrow \inf) vortex river networks dominate. For higher pinning f_p's, the Hortonian rivers become braided when B grows. For samples with higher pinning, it is the initial front (with low local density of field lines B, B < 3 B_{\phi} / 2, and thus dominant pinning force f_p) which branches out in a Hortonian manner. Behind this initial front follows the (intermediate-B) braided region. Further behind, follows the (large-B) dense-flux regime. The inset shows the shift in the Horton-braided boundary f_p = 3 f_0 as the pinning density, n_p, is changed. As n_p is increased, the Horton-braided boundary shifts towards higher B. The broad crossover boundaries are in the region of triangles and rhombuses. The (power-law fit) lines are just guides to the eye. The dense-braided crossover at high-fields (dashed) is an extrapolation of the power-law fit for low fields; the former is very difficult to compute because it requires a large number of vortices monitored over very long times.

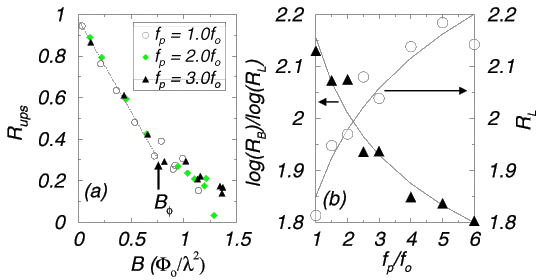
(a) Fraction R_{ups} of unoccupied pinning sites (ups) versus B for six samples with different f_p's. (and five realizations of disorder for each f_p). We find a change in the rate at which pins become occupied with increasing B: it decreases noticeably for B > B_{\phi}. (b) The length ratio R_L and fractal dimension D_F = d_c \log{R_B} / \log{R_L}, versus the pinning force, f_p. Here, the average stream dimension, d_c, is one. Only the trends in R_L and D_F can be observed here because their error bars are +/- 0.05. The lines are power-law best fit curves, which only provide a guide to the eye. The formula for D_F, namely D_F / d_c = \log{R_L} / \log{R_B}, gives values slightly above the space-filling value of 2, because it assumes that Horton's laws hold at all length scales, while our vortex basins only span a very limited range of length scales. Open circles: The length ratio R_{L} versus the pinning force f_p. Filled triangles: The ratio D_f / d_c versus f_p. The lines are best fit curves.

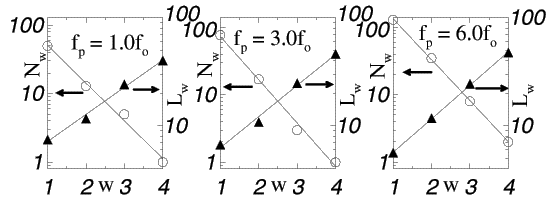
The number of streams N_w of order w, and their lenghts L_w, for vortex river networks with three different pinning forces f_p. Six different f_p's gave virtually identical plots---all obeying Horton's laws. Open circles indicate the number N_w of streams with order number w. Filled triangles indicate the average length L_w of streams with order number w.