We study stochastic transport of fluxons in superconductors by alternating current (AC) rectification. Our system provides a fluxon pump, "lens", or fluxon "rectifier" because the applied electrical AC is transformed into a net DC motion of fluxons. Thermal fluctuations and the asymmetry of the ratchet channel walls of the simulated samples induce this "diode" effect, which can have important applications in devices, like SQUID magnetometers. While many of the behaviors observed are consistent with previously studied one-dimensional (1D) ratchets, certain features are unique to this novel 2D geometric rectifier.



Unless otherwise specified, each figure refers to simulations conducted in the following way: Initially fluxons were randomly placed inside the channel and subjected to an alternating current along y --- producing a square-wave Lorentz driving force along x with F º f_L / f₀ = 15, and period P = 2 t (here, t = 100 MD steps). This means that in the absence of thermal noise (T = 0) and channel walls, a single fluxon would alternate traveling 15 l (where l is the Landau penetration depth) in one direction (e.g., +x), and then 15 l in the other (-x).  The period 9 l of the horizontal ratchet teeth was such that the driving force F = 15 should be sufficient to allow for a rectification, or diode effect, because it moves the fluxon back and forth through the bottlenecks indicated in the inset of Fig. 1. Ten runs, of 250 000 MD steps each, were used to find the average current and standard deviation for each plotted point. When a standard deviation is not shown, it was significantly smaller than the plotted point.  All samples had a 2D geometric ratchet made of asymmetric walls.  The simulated sample was an 18 l by 18 l square, with periodic boundary conditions. The channel is 7 l wide, with saw-teeth of period 9 l (four teeth per unit cell) and slope 1/3 (except in Fig. 5 where geometry was varied).  This leads to a bottleneck that is one l wide.  This construction is a novel 2D ratchet that uses geometry, instead of potential energy, to cause rectification.



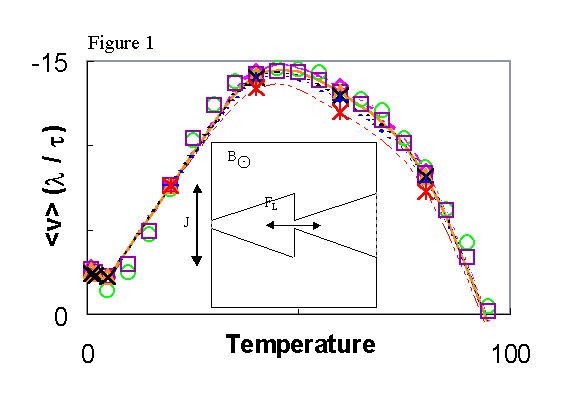Temperature dependence of the fluxon rectification. --- Figure 1 shows the rectified average fluxon velocity <v>, which can be measured as a voltage, versus temperature T for the ratchet geometry in the inset.  The magnetic field B is directed out of the figure.  J is a vertically applied alternating current square-wave that drives the fluxons back and forth horizontally along the channel.  The number of fluxons is: 1, circle; 25, diamond; 50, box; 75, triangle; 100, times; 150, plus; 250, asterick.The dimensionless temperature T was varied over two orders of magnitude, from 1 to 100.

These simulations clearly indicate an optimal or "resonant" temperature regime in which the DC fluxon velocity is maximized by the fluxon pump or diode.  This optimal temperature regime can be explained as a trade-off between allowing the fluxons to fully explore the ratchet geometry (i.e., T must not be too low) and washing out the driving force (i.e., T must not be too large).  At low temperatures, the alternating driving force will cause a fluxon to migrate to the center of the channel and no longer be impeded or assisted by interactions with the geometry; while at high temperatures the driving force becomes irrelevant and thus the fluxon is no longer pushed through bottlenecks regularly.  The <v>(T) curve for many randomly placed fluxons is similar to the single fluxon case, but the magnitude of <v>(T) decreases when the fluxon density B increases.  This is because the repulsive force produced by a large number of fluxons act to restrict each other's motion.  Note that at the optimal temperature, the fluxons travel nearly 15 l every 100 MD steps.  The general shape of the curve was established with two fine scans with one and fifty fluxons.  Conformity of other field strengths to this curve was judged by performing a coarser scan, then connecting the points with a spline.  The small dip in the <v> for low T will be discussed separately (see Fig. 3 below).

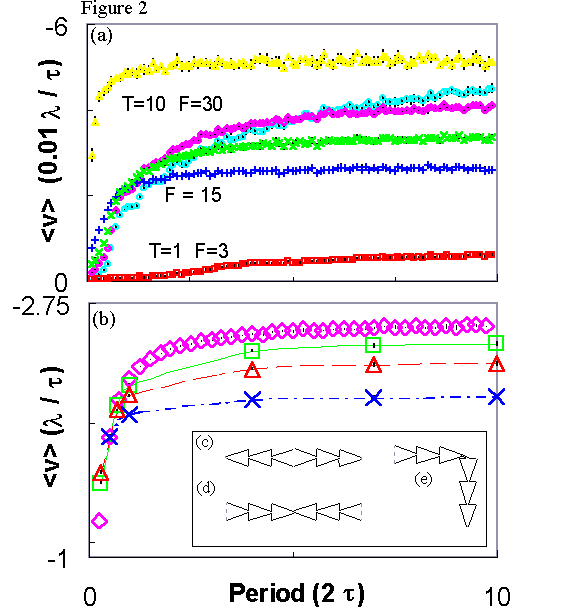Driving period dependence of the flux pump. --- Average fluxon velocity <v>, versus driving force period P for (a) one fluxon and (b) many fluxons. For very low periods little rectification occurs, and for higher periods, <v> slowly increases.  The four F=15 curves in the middle of (a) show similar behavior and correspond to (top to bottom at t = 10): T=1, bullet; T=2, diamond; T=3, times; T=2, plus. In (b), similar <v> occur for 50 (diamond), 100 (box), 150 (triangle), and 250 (times) fluxons.

Fig. 2(a) shows <v>(P) for six different combinations of driving force amplitudes F and temperatures T for a single fluxon.  Interestingly, as the period P of the driving force was varied from low to high (from P = 20 MD steps to 2000 MD steps) no optimal peak in <v> was discovered.  This is in contrast with previous work on ratchets, which provide a peak in <v> versus either P or frequency.  Instead, we find that while a high frequency driving force yields a very small ratchet velocity, the velocity quickly converges to a nearly stable value with increasing P.  This result corresponds to the idea that a fluxon must be forced through the bottleneck of the geometric 2D ratchet in order for it to be a rectifier.  At high frequencies, a fluxon does not travel far enough to interact with the bottleneck.  Once the frequency is low enough to force it through a bottleneck, however, the net velocity changes little by forcing it through further bottlenecks.

All of the simulations in Fig. 2(a) were conducted at relatively low temperatures to allow the effects of the driving force to dominate.  In addition to trying F = f_L / f₀ = 15, the value typically used in this paper, two combinations of driving force and temperature magnitudes were tried that both also had an F/T ratio of 3/1.  While varying P at the low-T regime had little effect upon the period dependence curve, varying F very clearly did have an effect: The higher F, the greater <v>.

Fig. 2(b) shows the dependence of <v> on P, for T = F / 3 = 5 with many fluxons instead of one.  Initially, fifty randomly placed fluxons were simulated.  As with the single fluxon case, a high frequency driving force resulted in a low <v> because the fluxons were not being forced through the ratchet bottleneck. Increasing P produced a rapidly plateauing <v>.  Once the shape of the curve was determined, similar sets of observations were made of different fluxon densities B at six different periods.  These simulations of many fluxons demonstrate that, as with one fluxon, there was no optimal peak.

The inset demonstrates a few constructs made possible by ratchets.  By coupling two ratchets that rectify in opposite directions, fluxon lenses that could either (c) disperse or (d) concentrate fluxons in chosen regions of a sample can be created.  Corners (e) can also be constructed.  Such remarkable devices, and modifications of them, would allow the transport of fluxons along complicated nanofabricated channels: a microscopic network of fluxon channels in superconducting devices.  This type of configuration could be very important to get rid of unwanted, trapped flux in SQUID magnetometers, and also move fluxons along channels in devices.



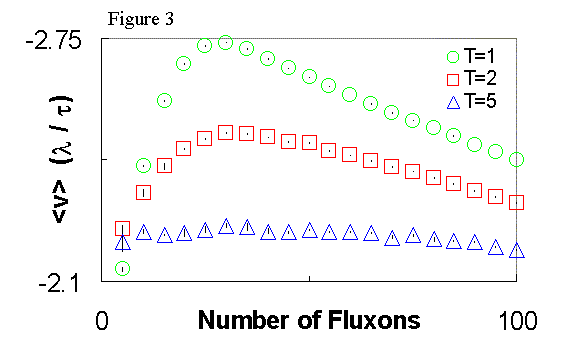Fluxon pump effect versus field. --- By varying the density of fluxons B, we found a maximum in <v> at very low temperatures (see Fig. 3). This is due to an enhanced interaction with the ratchet geometry: at extremely low T the driven fluxons eventually work their way to the middle of the channel and then no longer interact with the ratchet. A small increase in B can drive fluxons from the middle of the channel, causing these fluxons to increase their interaction with the sawteeth, without significantly increasing the resistance due to fluxon-fluxon interactions. Aside from this low-T resonance, increasing B slowly decreases <v>, because, as the fluxons repel one another, at high densities they block the bottleneck.  At high-temperatures (e.g., T = 50) the ratchet velocity decreases slowly with increased fluxons. In this case, the slight maximum in <v> found at low T is not present because the resistance due to fluxon-fluxon interactions is always larger than the gains from increased exploration of the geometry of the ratchet.



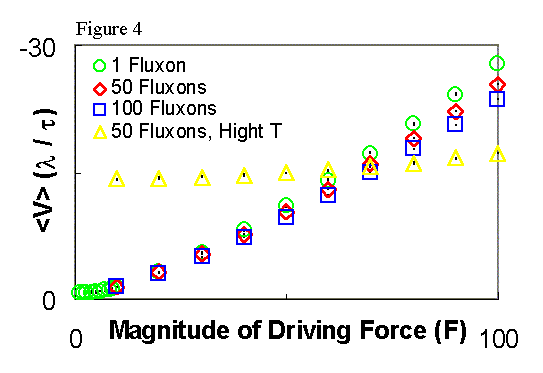Flux pump response to the driving force. --- Increasing the amplitude F of the square-wave driving force increases the average velocity <v> of a fluxon in the ratchet, as shown in Fig. 4.  This monotonic increase in <v> versus F for 2D geometric ratchets is different from the peak observed in 1D potential ratchets.  This makes it fairly easy for any particular 2D geometric ratchet to be continuously tuned to desired values of <v>.  This would be an advantage of 2D geometrical over 1D potential ratchets for potential practical designs of devices.  A reason for their different response is because the resistance to motion due to successive bottlenecks does not add like the resistance due to successive potential barriers.

If a fluxon happens to remain for some time in the center of a bottleneck, unlikely to happen at high-enough temperatures, then it will not be rectified; while the potential barrier rectifies at every period. Increased fluxon density again increases resistance, reducing <v>.



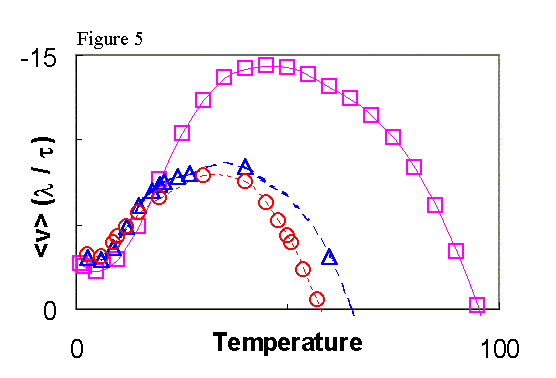Geometry dependence. --- To determine the generality of the simulation results presented here with respect to varied ratchet geometries, in Fig. 5 we compare <v>(T) for fifty fluxons in two alternate geometries with the <v>(T) shown in Fig.1 (open squares in both figures).  The geometries are characterized by (S, P_st), where S is the slope with respect to x, and P_st the spatial period of the sawtheeth.  The curves shown correpond to (1/3, 9), box; (2/3, 9/2), triangle; and (1, 3), circle.  Increasing the slope, and correspondingly decreasing the period, of the saw-teeth clearly shifts the optimal temperature to lower values.  Despite this shift, however, the qualitative behavior of the first geometry studied carried over to other ratchet slopes and periods. Additional samples and parameters, including wider bottlenecks, were also studied (but not discussed here due to space limitations), giving consistent results.



* Corresponding author.