|
Contra is a publicly available code that calculates the
contraction of a dark matter halo in response to condensation of
baryons in its center. The code is based on the modified
contraction model of Gnedin et al. (2004).
 The following assumptions are made: The mass distribution of
a dark matter halo is spherically symmetric and the velocity
distribution is isotropic. The final baryon distribution does not
need to be spherical. The code also calculates a line-of-sight
velocity dispersion for a tracer population with a given density
profile and velocity anisotropy (isotropic, constant
The following assumptions are made: The mass distribution of
a dark matter halo is spherically symmetric and the velocity
distribution is isotropic. The final baryon distribution does not
need to be spherical. The code also calculates a line-of-sight
velocity dispersion for a tracer population with a given density
profile and velocity anisotropy (isotropic, constant
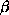 , Osipkov-Merritt, or
Mamon-Lokas model). , Osipkov-Merritt, or
Mamon-Lokas model).
Input options: There are two ways of specifying the initial
dark matter distribution and the final baryon distribution.
(i) Analytical distributions commonly used in astronomy: NFW,
Exponential, Hernquist, Jaffe, Sersic, or generalized Spherical
Sersic models. Tracer population can be one of the above profiles
or a power law with a given slope. (ii) Numerical
distributions in an optional input file.
Units: G=1, Rvir=1, Mvir=1 for
analytical distributions. For numerical input profiles, the unit of
mass is arbitrary but the radii should be in units of the virial
radius. All output quantities are in the input units, i.e.
the velocity unit is (GMvir/Rvir)1/2.
If you use this code for a publication, please acknowledge the
original paper of the modified model:
O. Y. Gnedin, A. V. Kravtsov, A. A. Klypin & D. Nagai, 2004, ApJ, 616, 16
"Response of dark matter halos to condensation of baryons:
cosmological simulations and improved adiabatic contraction model"
|
|
Download contra here
NOTE: a new version of Contra with adjustable parameters A and w, referenced in
O. Y. Gnedin, D. Ceverino, N. Y. Gnedin, A. A. Klypin, A. V. Kravtsov, R. Levine, D. Nagai & G. Yepes, 2011, ApJ, submitted
"Halo Contraction Effect in Hydrodynamic Simulations of Galaxy Formation",
is included in this distribution.
The User Guide will be updated shortly and will explain the usage.
|
|
|
Contra User Guide (PDF)
Install:
Untar the distribution and type make. It will create an
executable contra.
Command line arguments:
contra MAC DM BAR TRACE ANIS c serdm fb rb serb ra [in_file]
MAC (model of adiabatic contraction) :
0 = standard model, 1 = modified model Gnedin et al. (2004), -1 = no contraction
DM (initial dark matter profile) :
1 = NFW, 2 = Navarro et al. (2004), 3 = truncated satellite (Kazantzidis et al. 2004)
BAR (final baryon profile) :
1 = Exponential disk, 2 = Hernquist model, 3 = Jaffe model, 4 = Sersic (same m as DM)
TRACE (tracer population) :
1 = Exponential, 2 = Hernquist, 3 = Jaffe, 4 = Sersic (same m as DM), <0 = slope of a power law
ANIS (type of anisotropy distribution) :
0 = isotropic, 1 = constant 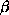 , 2 = Mamon-Lokas, 3 = Osipkov-Merritt , 2 = Mamon-Lokas, 3 = Osipkov-Merritt
c = initial halo concentration parameter, Rvir/rs
serdm = index of a spherical Sersic profile for dark matter
fb = baryon fraction within the virial radius, Mb/Mvir
rb = final baryon scalelength, rb/Rvir
serb = index of a Sersic profile for baryons (if TRACE=6), otherwise baryon truncation radius
ra = radius of velocity anisotropy for tracer population,
ra/Rvir
(or 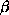 , for ANIS=1) , for ANIS=1)
in_file = (optional) file with numerical profiles for initial dm and final baryons
six input columns:
ri, mbi, mhi, rbf, mbf,
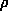 tr tr
Note: the calculation of the line-of-sight velocity
dispersion is the most computationally intensive part. If the
dispersion is not needed, set TRACE=0 to avoid its
computation.
Output:
ri = initial grid of radii
rf = contracted radii
mi = initial dark matter mass enclosed within ri
mf = final dark matter mass enclosed within ri
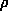 i
= initial dark matter density at ri i
= initial dark matter density at ri
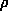 f
= final dark matter density at ri f
= final dark matter density at ri
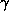 i
= initial logarithmic slope of dark matter density at ri i
= initial logarithmic slope of dark matter density at ri
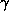 f
= final logarithmic slope of dark matter density at ri f
= final logarithmic slope of dark matter density at ri
Vc = circular velocity at ri
 los
= line-of-sight velocity dispersion of the tracer population at ri los
= line-of-sight velocity dispersion of the tracer population at ri
|
 The following assumptions are made: The mass distribution of
a dark matter halo is spherically symmetric and the velocity
distribution is isotropic. The final baryon distribution does not
need to be spherical. The code also calculates a line-of-sight
velocity dispersion for a tracer population with a given density
profile and velocity anisotropy (isotropic, constant
The following assumptions are made: The mass distribution of
a dark matter halo is spherically symmetric and the velocity
distribution is isotropic. The final baryon distribution does not
need to be spherical. The code also calculates a line-of-sight
velocity dispersion for a tracer population with a given density
profile and velocity anisotropy (isotropic, constant
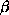 , Osipkov-Merritt, or
, Osipkov-Merritt, or
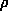 tr
tr
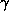 i
= initial logarithmic slope of dark matter density at ri
i
= initial logarithmic slope of dark matter density at ri los
= line-of-sight velocity dispersion of the tracer population at ri
los
= line-of-sight velocity dispersion of the tracer population at ri