Continuity and Differentiability

Daniel N. and Austin P.

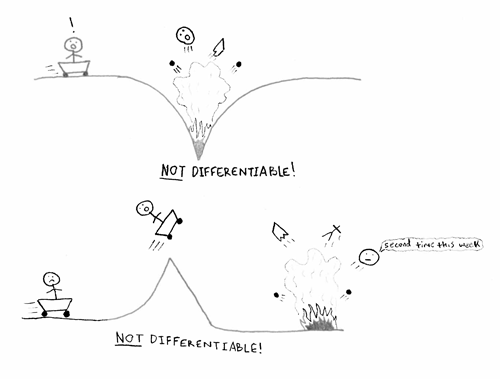
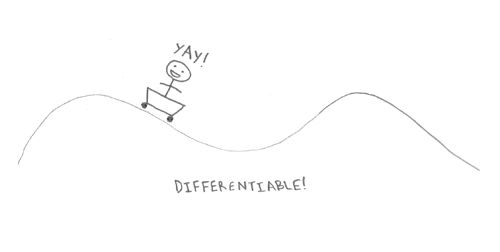
Think about a function as a roller coaster. If the function that defines the ride is continuous, you will have a great time! But, if it is not continuous there is, you will slightly fall off the track to a perilous end. If it is not differentiable that means there is a sharp bend in the track that will ultimately lead to whiplash.



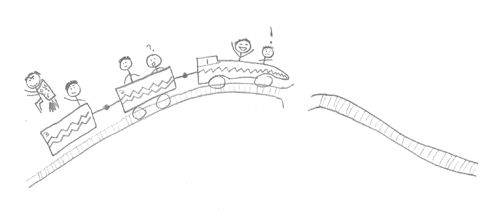
The blueprints for one roller coaster, called The Function, define the track by the equation:
$$f(x)=(x-a)(x+b)/(x-c)$$
where $a$,$b$, and $c$ are constants.



Is this track safe for passengers? Describe why it is or isn't.

Because $(x-c)$ is in the denominator there is a vertical asymptote there. Therefore the track is discontinuous.

Your manager, Archibald, wants to build a whole new roller coaster called, The Derivative of The Function. This track has an underground portion where $f(x)$ is less than zero. If The Function is increasing between $x=3$ and $x=6$ and decreasing between $x=6$ and $x=20$, when is the ride The Derivative of The Function below ground? * It is below ground between $x=6$ and $x=20$ because the slope of The Function is negative between those values.

With the information provided along with the fact that between $x=0$ and $x=3$ The Function runs parallel to the ground and that when $x$ is greater than 20 the slope increases again, draw the track of The Derivative of The Function. And determine if The Function is continuous. If it is not, make sure to mark your graph accordingly.


Between 0 and 3, the derivative would be zero but at three it is positive because the original is increasing. At $x=6$ the derivative would be negative because the original decreases. After 20 it would once again be positive. There are numerous ways to draw this track, but due to the fact that at x=3 the derivative goes from zero to positive, there is a sharp corner or a discontinuity. So, it is not differentiable. This means that at the points that it is not differentiable, the derivative must be marked with open circles.