Non-Newtonian fluids in the Faraday system
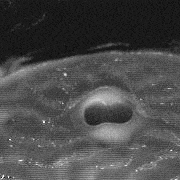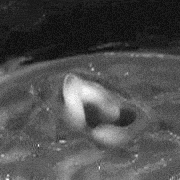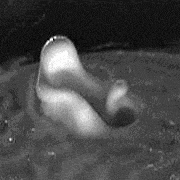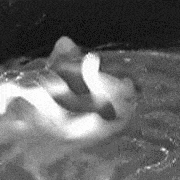

A Newtonian fluid subjected to parametric excitations develops wave patterns first described by Faraday. These waves are parametric excitations of waves a liquid surface can sustain. We study non-Newtonian fluids in the Faraday system, namely particulate suspensions, worm-like micellar solutions, emulsion. We find that these sustain a variety of soliton-like excitations (see example), and propose a theory of these based on hysteresis of the rheological properties and the ability of these fluids to sustain normal stresses.
Publications
- C. Falcon, J. Bruggemann, M. Pasquali and R. D. Deegan, "Localized structures in vibrated emulsions", Europhysics Letters 98, 24002 (2012)
- T. Epstein & R.D. Deegan, "Strip waves in Vibrated Shear-thickening Worm-Like Micellar Solutions ", Phys. Rev. E. 81, 066310 (2010). See also Kaleidoscope Images
- R.D. Deegan, "Stress hysteresis as the cause of persistent holes in particulate suspensions", Phys. Rev. E. 81, 036319 (2010)
- F. Merkt, R.D. Deegan, D. Goldman, E. Rericha, & H.L. Swinney, “Persistent holes in a fluid”, Phys. Rev. Lett. 92184501 (2004)



