Other Links

Institute for Social Research, Survey Research Center (U-M) "Monitoring the Future" Study and its sampling methodology

THE 2000 US CENSUS the 2000 Census questionnaires (both short and long forms) 2000 Census plans and operations

Some sources and readings on survey research:

course electronic reserve readings:
Babbie, Earl. "Ch. 4 Research Design, Ch. 5 Conceptualization, Operationalization and Measurement" in The Practice of Social Research. 9th edition, Belmont, CA: Wadsworth, 2003, pp. 90 - 147. [pdf]

Fowler, Floyd. "Sampling," in Survey Research Methods. 2nd edition, Sage, 1993, pp. 10-37. [pdf]

Nishikawa, Nancy . "Ch 2: Survey Methods for planners," in The Planner’s use of information, edited by Hemalata C. Dandekar Chicago, IL: American Planning Association, 2003, pp. 51-78. [pdf]

see also:
Babbie, Earl. 1994. The Practice of Social Research. 7th ed. Belmont, CA: Wadsworth.
Bailey, Kenneth D. 1987. Methods of Social Research. 3rd ed. New York: Free Press.
Dillman, Don A. 1978. Mail and Telephone Surveys. New York: Wiley.
Fowler, Floyd J. Jr. 1993. Survey Research Methods. Beverly Hills: Sage Publications.

1. Introduction to Survey Research

Survey Research -- a form of observation Why sometimes seen as boring: often associated with consumer attitudes, preferences, and other seemingly mundane topics questions often very simple and "dumbed down" to fit into a questionnaire format the design of survey research involves lots of minute details -- crucial when you are actually designing a survey, but boring in the abstract while sitting in a classroom  Why surveys sometimes fail -- several common mistakes: pick the wrong sampling strategy low response rate bad questionnaire:  too long, asked the wrong questions, etc. lots of data but no easy way to analyze

Some basic terms: primary data:  data that you collect (e.g., through a survey, an interview, etc.) -- that is, collecting original data. secondary data:  data that has already been collected by someone else (e.g., the US Census)  census:  "(1) a count of the population and a property evaluation in early Rome;  (2) a usually complete enumeration of a population..."  (Merriam Webster's 10th) sample: [ME, fr. MF essample, fr. L exemplum -- more at EXAMPLE]  "(1) a representative part of a single item from a larger whole or group esp. when presented for inspection or shown as evidence of quality:  SPECIMEN  (2) a finite part of a statistical population whose properties are studied to gain information about the whole"   (Merriam Webster's 10th) sample (N) vs. population (M) sampling fraction = N/M questionnaire survey instrument respondent unit of analysis longitudinal vs. cross-sectional panel survey Heisenberg Uncertainty Principle  -- for research, this implies that one cannot observe with disturbing in some way the observed.

The Culture of survey research: Conducting a survey is a form of communicative inquiry -- of asking questions. Both communication and inquisitiveness are shaped by culture. therefore the questions we ask (survey questions) the reasons we ask them (theory and hypotheses) the way we ask them  (survey design -- e.g., over the telephone, in-person on the street) whom we ask  (the sample) and the way they are answered (responses) are embedded in the culture where we live and work.  as a result, survey research is both a science and a social activity (a dialogue), and cannot be easily exported from one place to another.    Examples:  questionnaires on environmental awareness in post Cold War Poland interviews of U.S. defense contractors (and open- vs. closed-ended questions;  exploratory vs. more focused questioning)

Key Themes: surveys take a lot of time:  only engage in primary research if secondary data is not available (e.g., no data, data too old, not for the people / places of interest, not the right variables, etc.) keep the survey simple and very straightforward:   the challenge is to ask simple, clear questions (with easily tabulated answers) that help us understand complex, often messy social issues. surveys are the confluence of statistics and human nature:   be scientific, but also socially perceptive you want to know the framework of results before you start designing the questionnaire.  Avoid asking questions without knowing what you will do with the answers.  Surveys should start with clear research and policy questions.

 

Steps of Survey Research: A Hypothetical Survey Research Schedule Q     Questionnaire Construction FC      Formatting and Coding S          Sampling PT      Pretest A        Analysis PR      Presentation

 
 
 
 

Ways to Administer Surveys:
This will shape your questionnaire, as well as your sample.
 

How the Questionnaire gets to the Respondent: a. in-person survey b. mail c. telephone d. internet

How they answer the questionnaire: 1.  self-administered 2.  administered by staff

see also Trochim on the plus and minus of survey methods
 
 

Some Advantages and Difficulties with Each Approach (ordered from low to high-tech)

	In-person	Mail Survey	telephone	internet
Advantages	higher response rates the most personable of the approaches lots of control over the process	cost savings:  no interviewers time savings questionnaire can be done at the respondent's convenience greater assurance of anonymity standardized wording (no interview bias) respondents can check records accessibility:  can reach anyone with a mail address	fast lower cost than face-to-face more anonymous than face to face can use wide geographic area random-digit dialing facilitates an unbiased sample Computer assisted technology both accelerates the process and allows for complex filtering	answers already in electronic format can allow for complex filtering questions very quick response time can reach anyone with access to a computer worldwide perhaps the quickest to fill out (especially if multiple choice)
Difficulties	can be costly, especially if covering a wide geographic area time-consuming can be expensive requires good training of interviewers	lack of flexibility:  no probing, no corrections, no soothing reluctant respondents low response rate no control over the environment no control over question order no control over who fills out the questionnaire no control over date of response cannot use complex questionnaire format (e.g., complicated filtering)	lots of resistance to telephone interviews can be confused with marketing needs to be fairly short no good for long questions, long lists of answer categories can take many tries to reach someone at home no visual materials possible	bias introduced -- only some people have access to computers.  how do you determine the population? low response rate hard to get long answers to open-ended questions (as compared to in-person or telephone) a mistrust of the way the data might be used (e.g., for marketing?)

 
 

Which way would you recommend administering each survey below?

Population	Topic	Mail Survey	In-person	telephone	internet
homeless in New York City	their diet and eating habits	no	yes	no	no
New Yorkers	their view of the homelessness	yes	yes	best?	?
U.S. city planners	their use of computers	yes	yes	yes	best?
typical Americans	reactions to the recent bombings in Afghanistan	too slow?	yes	yes	no?
prisoners	prison life	yes	yes	?	no
New York subway riders	crime on the subway
Chicago residents	attitude about the Sears Tower
Chicago residents	attitude about a new proposed skyscraper design
8-year-old children in Ann Arbor	their favorite public places to play
8-year-old children in Mozambique	their favorite public places to play
college students	their feelings about racism
Muscovites	their views on Putin and democracy in Russia
U.S. Senators	their support of recycling laws
married women	their fear of violence from their husbands
college students	their recognition of 100 book titles

 
 

2. Sampling

What is Sampling Based on?   The Concepts of Probability and Randomness

that is, the probability of each individual being included in the sample.
We assume that randomness (random sampling) creates an equal chance of each element being selected.
 

A sample will be representative if all members of the population have an equal chance of being picked.

 
 

Sample Size
depends on:

• nature of the population
• purpose of study
• use of subcategories
• heterogeneity of the population:  the greater the diversity (e.g., standard deviation), the larger the sample size needed.

Sampling Fraction -- or -- why do we usually just care about the sample size, not the population size?
sample (N) vs. population (M)
sampling fraction = N/M

the actual formula for the standard error (standard deviation of the sampling distribution) is:

where f = sampling fraction = N / M

but since typically M >> N
then f --> 0

so 1-f becomes 1, and so the formula for the standard error becomes:

Comparison of Corrected and Uncorrected Standard Error Calculations of a Hypothetical Population of 38,000 (and standard deviation of 20,000).
 

sample size (n)	Population size (m)	sampling fraction (f)	standard deviation of the sample	std error (corrected)	std error (uncorrected)	Percent difference between corrected and uncorrected standard error
1	38,000	0.00003	20,000	19999.7	20000.0	0.00%
100	38,000	0.00263	20,000	1997.4	2000.0	0.13%
200	38,000	0.00526	20,000	1410.5	1414.2	0.26%
400	38,000	0.01053	20,000	994.7	1000.0	0.53%
800	38,000	0.02105	20,000	699.6	707.1	1.06%
1,600	38,000	0.04211	20,000	489.4	500.0	2.13%
3,200	38,000	0.08421	20,000	338.3	353.6	4.30%
6,400	38,000	0.16842	20,000	228.0	250.0	8.81%
12,800	38,000	0.33684	20,000	144.0	176.8	18.57%
25,600	38,000	0.67368	20,000	71.4	125.0	42.88%
37,999	38,000	0.99997	20,000	0.5	102.6	99.49%
38,000	38,000	1.00000	20,000	0.0	102.6	100.00%

Note that there is very little difference in using the corrected vs. uncorrected standard error until the sampling fraction gets large.  For example, even with a sample of 800 (out of a total population of 38,000), the difference is only 1 percent.  The two estimates of standard error only begin to deviate significantly when the sample size is more than several thousand (that is, when the sampling fraction approaches about 10% or more).

Moral of the story:   it is fine -- and more conservative -- to use the uncorrected estimate, which is easier to calculate anyway.
 
 

Constructing the Sampling Frame:  the actual list of units from the population from which a sample is selected (e.g., the membership list from the American Planning Association;  the New York City phone book)

A door-to-door survey was conducted in various U.S. suburban areas.
One survey question was:  "Would you prefer to live in a higher density town with more public transit, more front porches, more walkable space, even if it means smaller houses and lots?"

In the population as a whole, 25 percent would have answered yes.

Can we know how biased the respondent sample will be as compared to the population as a whole?
Answer?   Only if we can know (or at least estimate) the preferences of the nonrespondents and of the population as a whole.

Example:  Given a specific response rate (e.g., 80%) and knowledge of both nonrespondent preferences
(e.g., 40%) and the total population's preferences (25%), we can know what the respondent sample mean will be (21%),
and thus how biased this is (4% too low).
 

Respondent sample mean as a function of Response Rate and Percent of Non-Respondents who would prefer the higher density town (if the population mean = (µ = 25%)
 

	Percent of Non-Respondents who would prefer the higher density town  (µ = 25%)
Response Rate	10%	20%	25%	30%	40%	50%	75%
95%	26%	25%	25%	25%	24%	24%	22%	high response rate
90%	27%	26%	25%	24%	23%	22%	19%
80%	29%	26%	25%	24%	21%	19%	13%
70%	31%	27%	25%	23%	19%	14%	4%
60%	35%	28%	25%	22%	15%	8%
50%	40%	30%	25%	20%	10%	0%
40%	48%	33%	25%	18%	3%
30%	60%	37%	25%	13%				low response rate
			no bias

One can express this table as a graph:

 

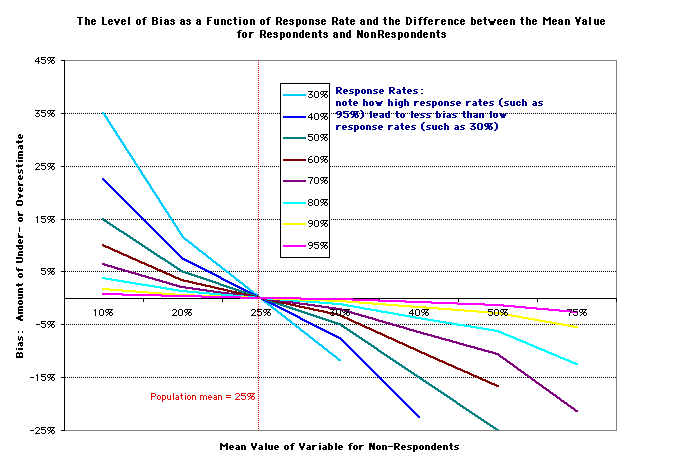
for more information on non-responses, see papers from the International Conference on Survey Nonresponse 1999
 
 
 

Two Approaches to Sampling:

• probability (where you can make assumptions about the probability of each case being selected -- e.g., that each case has an equal chance of being selected)
• nonprobability (where you cannot make these assumptions)

probability sampling

simple random sample (sampling without replacement -- that is, no-one can be picked twice)
Construct a list (a sampling frame) of the study population and randomly select, say, 100 individuals.

Each person, regardless of groupings, has an equal chance of being selected.

this is the ideal type;  but often hard to achieve.  It sounds easier than it is to do.
Why?  can you directly obtain a sampling frame?  (an actual list of sampling units).   Sometimes it doesn't exist, and to create it would be a terribly massive, frustrating undertaking.

Example:   how would you randomly sample and interview 50 people who might shop at Krogers over a given day using random sampling.
or:   randomly sample 100 Americans (would require a list of 274 million names).
 

A simple random sample of 20 cases

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100
101	102	103	104	105	106	107	108	109	110
111	112	113	114	115	116	117	118	119	120
121	122	123	124	125	126	127	128	129	130
131	132	133	134	135	136	137	138	139	140
141	142	143	144	145	146	147	148	149	150
151	152	153	154	155	156	157	158	159	160
161	162	163	164	165	166	167	168	169	170
171	172	173	174	175	176	177	178	179	180
181	182	183	184	185	186	187	188	189	190
191	192	193	194	195	196	197	198	199	200

A systematic random sample of 20 cases

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100
101	102	103	104	105	106	107	108	109	110
111	112	113	114	115	116	117	118	119	120
121	122	123	124	125	126	127	128	129	130
131	132	133	134	135	136	137	138	139	140
141	142	143	144	145	146	147	148	149	150
151	152	153	154	155	156	157	158	159	160
161	162	163	164	165	166	167	168	169	170
171	172	173	174	175	176	177	178	179	180
181	182	183	184	185	186	187	188	189	190
191	192	193	194	195	196	197	198	199	200

 

1. divide the population into strata (non-overlapping groups, hopefully fairly homogenous)
2. select a random sample from each strata (they need not be rank-ordered
3. aggregate (combine) the results from the strata to make inferences about the population

Over sampling leads to weighted samples, thus the use of weights.
The weight is proportional to the number of individuals in the population as a whole that each case in the sample "represents."

If you see weights for each case in a data set, that is an indication of a stratified survey with differential probabilities of each case being selected.
(Don't ignore the weights -- otherwise you will create biased estimates of the population.)

Stratified Sampling can also lower sampling error,
but only when the variable(s) used to stratify the data (e.g., faculty rank) are statistically related to the variables in the sample (e.g., faculty salaries).
 
 

Example:   use of weighted stratified sampling
a survey of planners, doctors and robbers in New York City.

Since planners and robbers both small subgroups of the population, a simple random sample would lead to only about 15 planners and 60 robbers included in the sample (too small to make accurate inferences about these subgroups -- especially planners)

Solution?
Divide into 3 occupational strata and over sample planners and robbers.   Since each strata has a different probability of being selected, use weights to adjust before aggregating to the population as a whole.

Visually, the 3 strata can be visualized as follows:

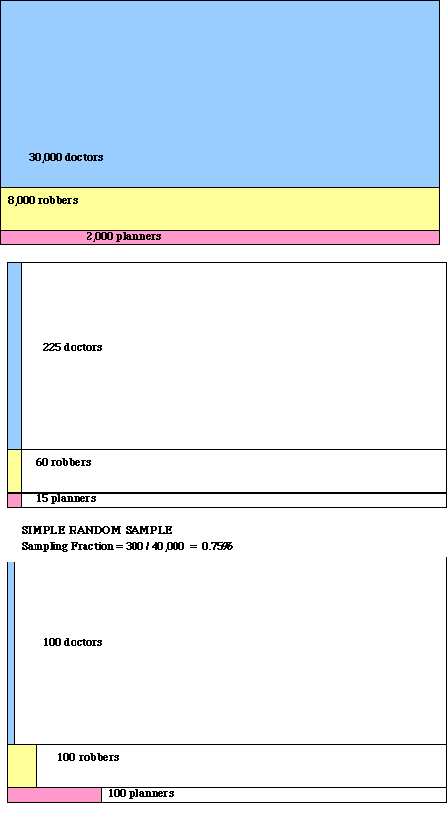
 0  ------  percent of each strata in sample ------>>>    100%

Above, one sees the effect of over-sampling planners (and undersampling doctors)

In table form:

	Population	Simple Random Sample (unstratified) n=300)	Stratified Sample n=300	Probability of Selection in Stratified Sample	Weight = 1 / probability of being selected
Planners	2,000	15	100	100/2000 = .05	20
Doctors	30,000	225	100	100/30000 = .0033	300
Robbers	8,000	60	100	100/8000 = .0125	80
TOTAL	40,000	300	300	---	---

How to interpret weights?   Each planner in the sample represents 20 planners in the population as a whole, while each sampled doctor represents 300 doctors in the population as a whole.
If you see survey data where all the cases have weights = 1, then no disproportional sampling.

1. determine one or more intermediate levels (sampling units) between the overall study population and the ultimate sampling elements.
2. for each level (sampling unit), take a random sample of each, and then a random sample within that larger "cluster", etc. (Since this process involves more than one stage or step of sampling, it is often called "Multistage Cluster Sampling".

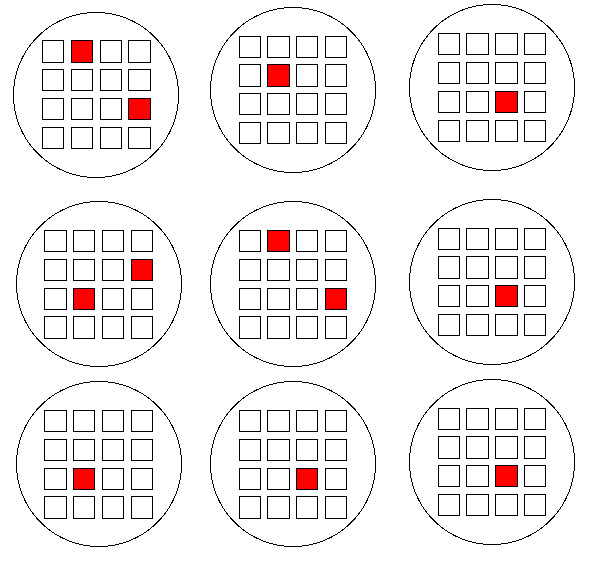
Example:  Imagine that you wanted to conduct in-person interviews with neighborhood organizations.
There are 9 cities scattered around the country with the relevant types of organizations, and 16 organizations within each of the 9 cities (or 144 total organizations).  You need to interview 12 organizations.  A simple random sample would likely require interviews in (and this travel to) these 9 distant cities:

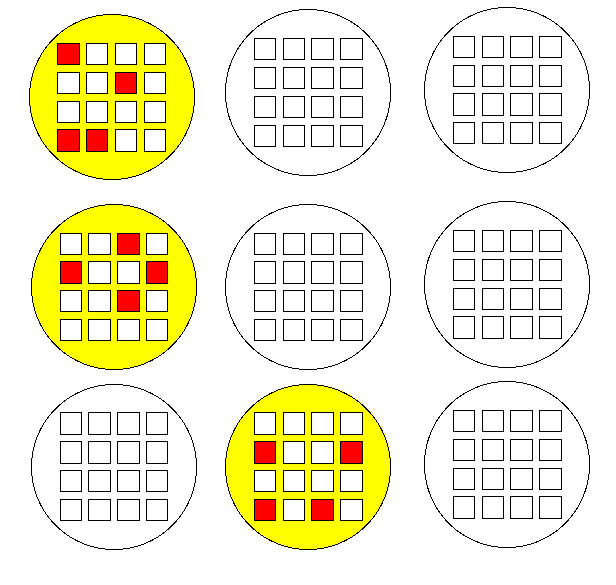
If you used multi-stage clustered sampling, you would first randomly select a certain number of cities (here three), and then randomly select four organizations within each of the three cities.  This saves travel time, and also makes it easier to assemble a sampling frame (a list of the ultimate sampling elements).

 
 

AN UNUSUALLY COMPLICATED EXAMPLE:  from United States to     8 states to        4 counties within each state to           4 school districts within each county to              4 schools within each district to                 3 classrooms within each school to                   5 students within each classroom.  (TOTAL number of sampling elements = 8 x 4 x 4 x 4 x 3 x 5 = 7680 students. each stage of sampling leads to the selection of a sampling unit (e.g., states, cities, schools).  the final stage is the actual selection of the sampling elements (school students).

Each stage also introduces sampling error (the chance that you might happen to pick the more urban states, the poorer counties, the richer schools, the brighter students, etc.).  With random sampling at 6 different stages, the chance for error is quite high.   To reduce this, you might reduce the number of stages.  For example:   go right from states to districts, and from districts to schools, and from schools to students.  Use only as many stages as needed to obtain the sampling frame.

So:  a trade-off:  clustered sampling makes some kind of survey research possible or at least easier, but you sacrifice some accuracy.
 

cluster and stratified compared:

nonprobability sampling

convenience
simply ask who is around (people sitting next to you on the bus, in the laundromat as you do your clothes, etc.)
as easy as it comes.

e.g., if Democrats were 60% of the population and Republicans were 40%, then ask, say, 120 Democrats and 80 Republicans.

danger:  potential of biased selection within these quotas.   (that is, biases based on other factors than party)

No need to make proportional.   just have at least 1 entry per cell.

EXAMPLE:

	Cities with Low Public Transit Use	Cities with high public transit use
Growing Cities	Phoenix	San Francisco
Declining Cities	Memphis	Philadelphia

allows for all pertinent combinations to be represented in a small sample, and hence allow for more in depth study of each.  (such as in case studies -- to be covered later in the semester)
 
 
 

one type:  reputational sampling.  select cases based on their reputation.
EXAMPLE:  a study interested in educational reform.   First select states, then districts within state, and then select schools that have the reputation of being innovative.
 

ask someone in the group, who then refers you to others in the group, etc.

good for deviant subcultures.  e.g., interviewing Hells Angels members, etc.
 
 
 
 
 
 

3. Measures and Indicators

Conceptualization: linking concepts to measures.

Conceptual summaries are based on real observations. (And yet observation is shaped by our mental preconceptions, so there is a two-way interaction between concepts and measures.)

face validity:  how well does the measure match the concept?

Danger: reification. "the process of regarding as real things that are not" [Babbie, 1994:  120]

Can everything be measured?  a philosophical question.  Babbie (110) argues that "... we can measure anything that exists. There are no exceptions. If it exists, we can measure it."  But others would say not.  There is often a difference between the ability to name something, to measure it, to understand it, and to affect it.   We sometimes falsely assume that just because we can name something and measure it, we therefore understand it.  (For example, it is far easier to measure crime, poverty, urban decline and urban despair than to understand it.)
 
 

EXAMPLE:  can everything be measured? Can we put a price on nature? (e.g., of a free flowing river) This raises a dilemma:  One may philosophically/ethically object to this, since it represents the commodification of nature -- the forced adaptation of nature into the human world of economic accounting and prices.  And yet the failure to price nature may lead to its undervaluation and exploitation.  So:  the economic value of a river may be a poor measure of its total "value" (ecological value, intrinsic value, etc.), but it may be the most practical solution.

 

Why are measures important?

• because we often confuse concepts with measures
• we often have no idea how to measure them
• or we use bad measures and then disprove a conceptual relationship when the measure is to blame

Why the gap between the data results and what you want to know?

• Complex indicators -- having more than one dimension.
• No obvious, easy measure that comes even close to the concept: so you use the best but still imperfect variable.
• Proxy variable: you know that there is a better variable out there (one than comes closer to showing a causal relationship), but you use this one as a kind of proxy because (a) it is easier to collect; (b) it's what you have. the best but still imperfect variable
• A controversial concept, so that there is no consensus on what the concept means, and therefore no easy agreement on what measures would fit.
• Over multiple periods of time
• Not standardized.

Some strategies to select and develop measures:

• begin by selecting a unit of analysis, a time-frame (one point in time, or multiple time periods),  a geographic location and a population.  These will all affect the selection of a measure.
• decide on a level of measurement:  nominal, ordinal, interval (ratio)
• use existing measures where available and appropriate --  it saves time and effort, and has the advantage of standardization.  But often this is not possible.
• some concepts are so complex (e.g., sustainability, livable city, urban despair, empowerment) that you must first more narrowly define them before being able to measure.
• divide the concept into dimensions.  For example, divide "citizen participation" into attitude, behavior and impact components.
• to make the various values of a measure more comparable, convert to standardized units:  e.g., per capita, percent of total, etc.

Other examples of complex concepts:
 

Concept	Unit of Analysis
Globalization	Cities
sustainability	Cities
High tech	Industry
Level of Economic development	City
Economic class	Person
Urban social alienation	person
Citizen participation	person
Productivity	person

 

interchangeability of indicators
sometimes you may want to, e.g., one is easier to collect than another.
They should have high correlations. Ideally perfect.

But a danger: sometimes we think certain indicators are interchangeable, but in fact they are different dimensions of a more complex, accurate indicator. (e.g., GPA and GRE scores for intelligence).
 
 
 
 

4. Constructing Questionnaires

[REFER to hypothetical schedule to show placement of questionnaire draft, testing, revision, coding, etc.]