geometry_tools is a Python package meant to help you work with and visualize group actions on hyperbolic space and projective space.

The package is mostly built on top of numpy, matplotlib, and scipy. Optionally, the package can use tools provided by Sage to perform (slow) exact computations.

geometry_tools can help you:

• perform numerical (or sometimes, exact) computations with objects in hyperbolic space, in multiple models (namely the Klein, hyperboloid, projective, Poincare, and half-space models)

• draw nice pictures in the hyperbolic plane, the real projective plane, and the complex projective line

• work with representations of finitely generated groups into $\text{O}(d,1)$, $\text{GL}(d,\mathbb{R})$, and $\text{GL}(d,\mathbb{C})$

• do hands-on computations with representations of Coxeter groups into $\text{GL}(d,\mathbb{R})$

• use finite-state automata to do some simple computations in word-hyperbolic groups

Some limited support for 3D figures is also provided (via matplotlib).

None of the functionality of this package is (mathematically) very deep. Mostly, the package just wraps more sophisticated tools in a way intended to make it easy to quickly draw good pictures in ${\mathbb{H}}^2$, ${\mathbb{H}}^3$, and $\mathbb{R}{P}^2$ and $\mathbb{C}{P}^1$.

A quick example

To draw a picture of a right-angled pentagon in the hyperbolic plane:

from geometry_tools import hyperbolic, drawtools
from numpy import pi

# make a right-angled pentagon
pentagon = hyperbolic.Polygon.regular_polygon(5, angle=pi/2)

# draw the pentagon
figure = drawtools.HyperbolicDrawing()
figure.draw_plane()
figure.draw_polygon(pentagon, facecolor="lightblue")

figure.show()

This code produces:

Installation

Right now, the easiest way to install geometry_tools is to download or clone the project from the git repository, and run

pip install .

from the directory where you've downloaded it. If you don't have pip installed, you should install pip first. Alternatively, you can try running python setup.py install from the project directory (this is not recommended).

Drawing hyperbolic group actions

The geometry_tools package is handy for drawing pictures of tilings in (\mathbb{H}^2). Here we will work with visualizing a (2,3,7) triangular tiling:

You can also download this example as a Jupyter notebook or a python file.

To get started, first instantiate the coxeter.TriangleGroup class to get a (2,3,7) triangle group, and compute its geometric representation into the isometries of the hyperbolic plane:

# get a representation for a triangle group.
# (these are built in to the program)
from geometry_tools import hyperbolic, coxeter, drawtools

triangle_rep = coxeter.TriangleGroup((2,3,7)).hyperbolic_rep()

We can draw the reflection walls for the group using the drawtools subpackage:

# find the fixed points at infinity for the generating reflections

reflections = triangle_rep.isometries(["a", "b", "c"])
walls = hyperbolic.Geodesic.from_reflection(reflections)

wall_a, wall_b, wall_c = walls

fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()

fig.draw_geodesic(wall_a, color="green")
fig.draw_geodesic(wall_b, color="blue")
fig.draw_geodesic(wall_c, color="red")

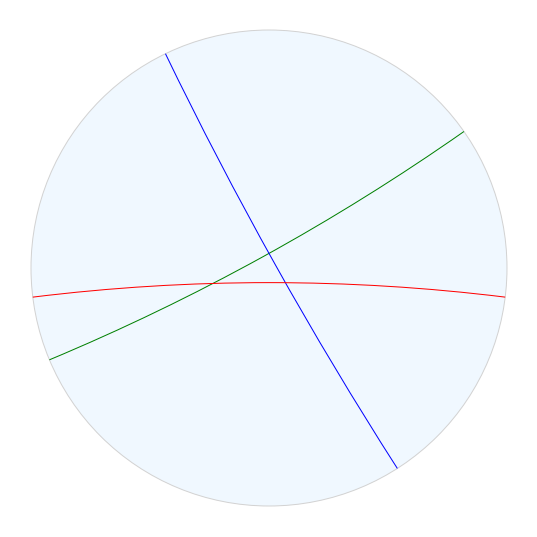
We can find a fundamental domain for the triangle group by taking the triangle whose vertices are the fixed points of length-2 elements of the group.

triangle_vertices = triangle_rep.isometries(["ab", "bc", "ac"]).fixed_point()

fund_triangle = hyperbolic.Polygon(triangle_vertices)

fig = drawtools.HyperbolicDrawing(model="poincare")

fig.draw_plane()
fig.draw_polygon(fund_triangle, facecolor="lightgreen")

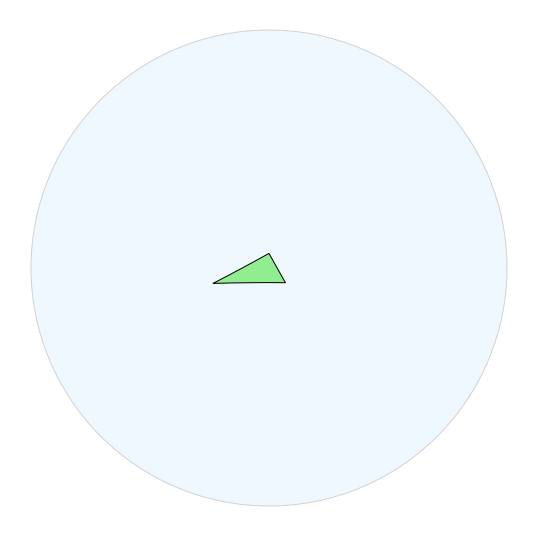
If we want to start visualizing the tiling of (\mathbb{H}^2) we get from this triangle group, we can start drawing translates of this fundamental domain. The easy (but less efficient and appealing) way to do this is to just draw copies of the fundamental domain translated by the images of freely reduced words in the group.

words = triangle_rep.free_words_less_than(5)
isometries = triangle_rep.isometries(words)

tiles = isometries @ fund_triangle

fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()

fig.draw_polygon(tiles, facecolor="lightgreen")

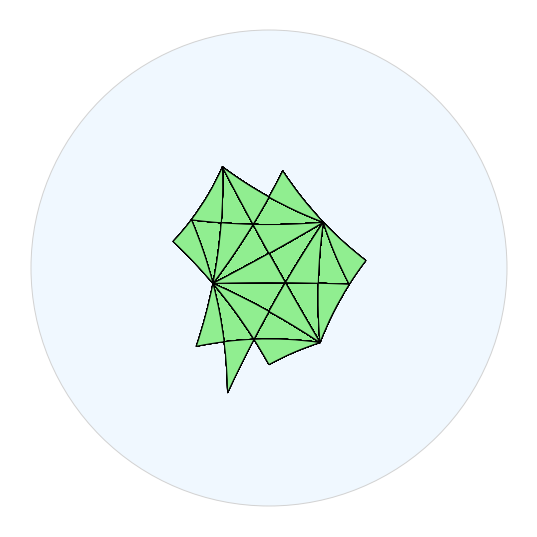
Speeding things up with finite-state automata

Drawing copies of the triangle translated by images of all freely reduced words is a little slow. And, we end up drawing the same triangle on top of itself many times. We can speed up the process by picking a unique word for each element of the group, using a finite-state automaton.

The geometry_tools.automata subpackage provides a handful of tools for working with finite-state automata. It can load and manipulate the automata generated by the kbmag program. While kbmag is not included with geometry_tools, the package does provide precomputed automata for a number of word-hyperbolic groups. To get the list of precomputed automata, import the automata.fsa submodule and call fsa.list_builtins(). Call fsa.load_builtin() to load an automaton.

Thanks to code provided by Florian Stecker, the geometry_tools package can also generate automata for any Coxeter group. So we can get an automaton for the (2,3,7) triangle group like so:

# construct the (2,3,7) automaton
triangle_fsa = coxeter.TriangleGroup((2,3,7)).automaton()

# get a unique word for each group element of length < 25.
# (we convert to a list since enumerate_words returns a generator)
words = list(triangle_fsa.enumerate_words(30))

free_words = list(triangle_rep.free_words_less_than(9))

# compare unique words of length <30 to freely reduced words of length <9.
# when we don't consider the relation, we get many redundant words!
len(words), len(free_words)

(5951, 585937)

To make the picture a little nicer, we can produce an automaton which only accepts words of even length. Then we can get the collection of all isometries which are images of words accepted by this automaton.

even_triangle_fsa = triangle_fsa.even_automaton()
pos_isometries = triangle_rep.automaton_accepted(even_triangle_fsa, 15)

tiles = pos_isometries @ fund_triangle

fig = drawtools.HyperbolicDrawing()
fig.draw_plane()
fig.draw_polygon(tiles, facecolor="royalblue", edgecolor="none")

To recap, here's all the code we need to produce the above picture:

from geometry_tools import hyperbolic, coxeter, drawtools

# make the triangle group representation
triangle_group = coxeter.TriangleGroup((2,3,7))
triangle_rep = triangle_group.hyperbolic_rep()

# find a fundamental domain for the action by finding 
# fixed points of length-2 elements
vertices = triangle_rep.isometries(["ab", "bc", "ca"]).fixed_point()
fund_triangle = hyperbolic.Polygon(vertices)

# find all orientation-preserving isometries of length at most 30 using an automaton
triangle_fsa = triangle_group.automaton(even_length=True)
pos_isometries = triangle_rep.automaton_accepted(triangle_fsa, 15)

# draw the translated triangles
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(pos_isometries @ fund_triangle, 
                 facecolor="royalblue", edgecolor="none")