By Shiming Duan, Last Update: 8/11/2010 3:03 PM
1.1 Motivation
As discussed in the book, time delay systems (TDS) arise from inherent time-delays in the components of the systems, or from the deliberate introduction of time-delays into systems for control purposes. Such time-delays occur often in systems in engineering, biology, chemistry, physics and ecology. Here we will provide two simple but well-known examples to show the presence of time delay.
Example 1.1 Hydraulic System
In Figure 1.1, a water tank and pipe with length L are shown. A linear model is considered for modeling the water tank:
![]()
where A is the cross-sectional area, ![]() is
the water density, g is gravitational acceleration, h is
the delay, t is time, R is the hydrodynamic resistance of the output pipe, uin
is the input flow rate and x(t) is the water surface level.
is
the water density, g is gravitational acceleration, h is
the delay, t is time, R is the hydrodynamic resistance of the output pipe, uin
is the input flow rate and x(t) is the water surface level.
The objective of the control is to maintain the level of water inside the tank at 0.5m. Assume a proportional state feedback control uin(t)=Kx(t), the closed loop system can be described via a delay differential equation (DDE):
![]()
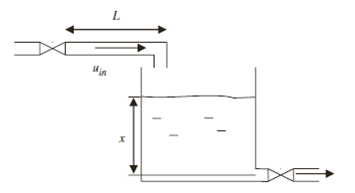
Figure 1.1. Water Tank (K. Moezzi, 2009)
Example 1.2 Pendulum Problem
Consider the equation of motion of a simple pendulum as follows:
![]()
where l is the length of the pendulum, g is gravitational
acceleration, m is the pendulum mass and T is the input torque. A
constant delay, h, between the sensor and the controller is considered
in the model. It is desired to keep the pendulum at ![]() .
One can show that, the nonlinear model can be linearized around
.
One can show that, the nonlinear model can be linearized around ![]() as
as
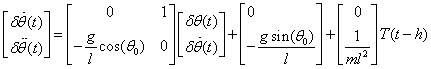
where ![]() .
The controller is designed to be
.
The controller is designed to be
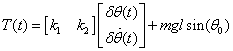
Thus, the closed-loop system can be described by the following matrix time-delay system:
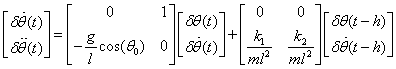
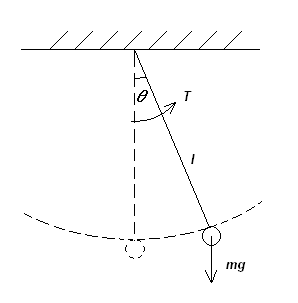
Figure 1.2 Pendulum System
Example 1.3 Modeling of Human Immunodeficiency Virus (HIV) Pathogenesis with an Intracellular Delay
For years people have been looking for accurate models based on differential equations for HIV pathogenesis dynamics. Such models can help in better analysis of the HIV pathogenesis and in designing better therapy regimes. As illustrated in Figure 1.3, the HIV infects target cells with a certain infection rate and causes them to become productively infected T-cells. Meanwhile, drugs (i.e., protease inhibitor) help inhibit the cleaving of viral polyproteins and render newly produced virions non-infectious with a certain effective rate. The immune system of the human also kills some of the infectious virions. Since it takes some time for the virus to enter a target cell and before the production of new virus particles, an delay (intracellular delay) is inherent in this biological process. When an intracellular delay is included, the models of HIV infection provide a more accurate representation of the biology since it better predicts the viral load dynamics.
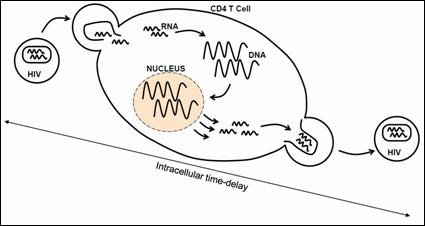
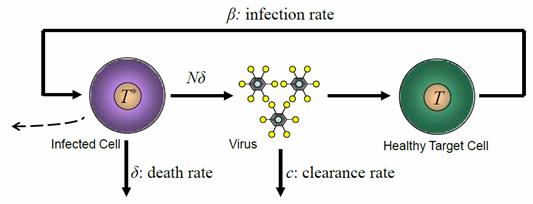
Figure 1.3 HIV-1 infects target cells (T) with a rate constant �� and causes them to become productively infected cells (T*). Time-delay results from the time between initial viral entry into a cell and subsequent viral production. (From Yi, et. al., 2010)
The HIV pathogenesis can be modeled via the coupled delay differential equations (Nelson et al., 2000).
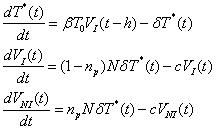
where t is the elapsed time since the treatment is initiated,
h is time-delay, T0 is the target T-cell concentration, T*
is the concentration of productively infected T-cell, VI
is the concentration of infectious virions in the plasma, VNI
is the concentration of non-infectious virions in the plasma, c is
rate of virion clearance, ![]() is
the rate of loss of the virus-producing cell, N is the mean number of
new virions produced per infected cell during its lifetime, and np
represents the drug efficacy of a protease inhibtor. It is assumed
that HIV infects targeted cells with a rate of
is
the rate of loss of the virus-producing cell, N is the mean number of
new virions produced per infected cell during its lifetime, and np
represents the drug efficacy of a protease inhibtor. It is assumed
that HIV infects targeted cells with a rate of ![]() and
causes them to become productively infected T-cell, T*.
and
causes them to become productively infected T-cell, T*.
The model can be further written as a matrix delay differential equation
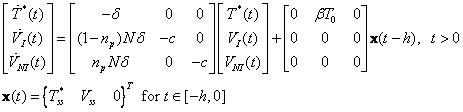
The parameters are estimated using the data from drug perturbation experiments (P.W. Nelson, et. al. 2001). For the detail of the modeling work, please refer to the Chapter 8 in the book.
|
Name |
Description |
Value |
|
T0 |
Target T-cell concentration |
408 cell mm-3 |
|
h |
Intracellular delay |
0.91 days |
|
|
Death rate of an infected T-cell |
1.57/day |
|
c |
Clearance rate of virus |
4.3/day |
|
N |
Bursting term for viral production after lysis |
480 virions/cell |
|
np |
Protease inhibitor efficacy |
0.7 |
|
|
Viral infectivity rate |
c/(NT0) |
1.2 Background
1.2.1 Delay differential equations
Time-delay systems can be represented by delay differential equations (DDEs), which are a type of differential equation where the time derivatives at the current time depend on the solution, and possibly its derivatives, at previous times. Here only retarded DDEs, where there is no time-delay in the derivative terms, are considered:
![]()
where
![]() and
and ![]() are
are ![]() coefficient matrices,
coefficient matrices, ![]() are
are ![]() coefficient
matrices,
coefficient
matrices, ![]() is an
is an ![]() state
vector,
state
vector, ![]() is an
is an ![]() input
vector,
input
vector, ![]() is an
is an ![]() preshape
function, t is time, and h is a constant scalar time
delay.
preshape
function, t is time, and h is a constant scalar time
delay.
1.2.2 Lambert W function
Definition: The Lambert W function, ![]() ,
first introduced in the 1700s by Lambert and Euler (Corless et. al.,
1996), is a complex valued function with a complex argument H and
an infinite number of branches denoted by k, where
,
first introduced in the 1700s by Lambert and Euler (Corless et. al.,
1996), is a complex valued function with a complex argument H and
an infinite number of branches denoted by k, where ![]() and satisfies
and satisfies
![]()
for all branches. The principal and all other branches of the Lambert W function can readily be evaluated using functions available in standard software packages such as Matlab or Mathematica.
Important Properties:
1. Figure 1.3 shows the range of each branch of the Lambert W function. For example, the real part of the principal branch, W0, has a minimum value, −1.
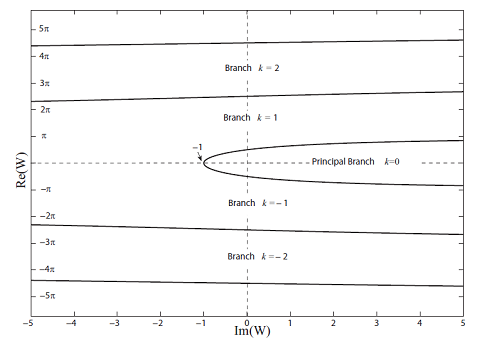
Fig. 1.3 Ranges of each branch of the Lambert W function (Corless et al., 1996). Note that real part of the principal branch, W0, is equal to or larger than −1.
2. The Lambert W function may be approximated using Newton's method:
![]()
3. The derivative and antiderivative of the Lambert W function can be evaluated using the equations below
![]()
![]()
4. The values of the principal branch, W0, of the scalar Lambert W function at certain points are listed
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(From Wikipedia)
Example 1.4 The Lambert W function can be used to solve the following equation for t:
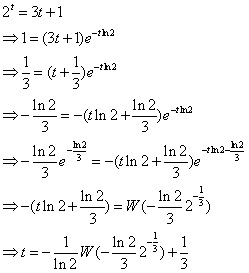
Links: Lambert W function - Wikipedia, the free encyclopedia
Lambert W-Function -- from Wolfram MathWorld
On the Lambert W Function (Corless et. al., 1993)
Matrix Lambert W Function
When the argument of the
Lambert W function is a square complex matrix, we can define a matrix Lambert W
function. The matrix Lambert W function can be calculated using similarity
transformations. If the argument, ![]() , of the
matrix Lambert W function
, of the
matrix Lambert W function ![]() is a
is a ![]() matrix, one needs to first transform H into Jordan canonical
form:
matrix, one needs to first transform H into Jordan canonical
form:
![]()
where J is the Jordan canonical form of H, and Z is the corresponding modal matrix. Then the Lambert W function value for each Jordan block can be obtained via the following equation (Pease, 1965):
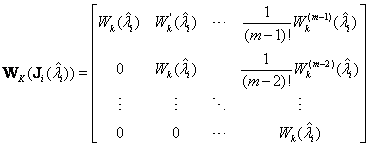
where ![]() is
an
is
an ![]() Jordan block and m is
the multiplicity of the eigenvalue
Jordan block and m is
the multiplicity of the eigenvalue ![]() .
Finally, one needs to transform the block diagonal matrix consisitng of Lambert
W function Jordan blocks back to the original basis:
.
Finally, one needs to transform the block diagonal matrix consisitng of Lambert
W function Jordan blocks back to the original basis:
![]()
Example 1.5 Compute  and
and

For ![]() , its Jordan canonical form can be written as
, its Jordan canonical form can be written as ![]() with the modal matrix
with the modal matrix ![]() satisfying
satisfying
![]() .
Since it has two distinct eigenvalues, it will have two Jordan blocks whose
Lambert W function values can be determined as:
.
Since it has two distinct eigenvalues, it will have two Jordan blocks whose
Lambert W function values can be determined as:
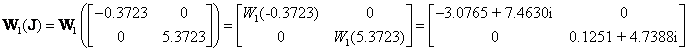
The matrix Lambert W function of H can be obtained as:
![]()
For  , it has a Jordan canonical form of
, it has a Jordan canonical form of 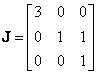 with modal
matrix
with modal
matrix 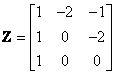 .
Note that it has a repeated
.
Note that it has a repeated
eigenvalue at -1 with the geometric multiplicity of one. Thus,
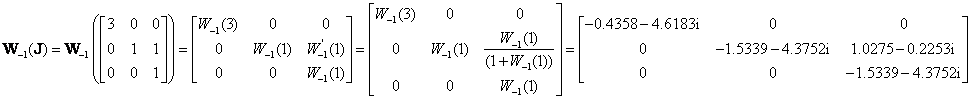
The matrix Lambert W function of H can be obtained as:

Remark: Note that the approach have for evaluating the matrix Lambert W function is analogous to the evaluation of the matrix exponential function.
Some Common Mistakes
a) exp(·) and expm(·) commands in matlab
In Matlab, one should use expm(·) instead of exp(·) to calculate the matrix exponential function
For exampl, if ![]() , the matrix exponential
functoin
, the matrix exponential
functoin ![]()
If one use exp(·) command to compute this, it will take the exponential function of each term of the matrix instead of treating the argument as a matrix.
Wrong way
exp([1 0;0 2])
ans =
2.7183 1.0000
1.0000 7.3891
Right way
expm([1 0;0 2])
ans =
2.7183 0
0 7.3891
b) eig(·) and jordan(·) commands
In order to calculate the matrix Lambert W function, one needs to transform the input matrix into Jordan canonical form and transform the results back after calculation. To realize such a similarity transformation, one can use either the eig(·) or the jordan(·) command if the matrix is diagonalizable. If the matrix is not diagonalizable, the eig(·) command will return an incorrect answer and one should use the jordan(·) command only.
A=[2 1;0 2] % an example of a matrix A, which is not diagonalizable
Wrong way
[v,d]=eig(A)
False=v*d*inv(v) % not same as A
False =
2 0
0 2
Right way
[v1,d1]=jordan(A)
Correct=v1*d1*inv(v1) % same as A
Correct =
2 1
0 2
Other Applications:
The Lambert W function is useful for the solution of DDEs, which is the subject of this book. However, it is also useful for other problems. Please see the links below.
Application to generation of generalized gaussian noise (François Chapeau-Blondeau and Abdelilah Monir, 2002)
Some applications to classical statistical mechanics (Jean-Michel Caillol, 2003)
Application to steady shearing flows of the Papanastasiou model (Z. You, R.R. Huilgol and E. Mitsoulis, 2008)
Application to Terrain-based Vehicle Localization(Sean Brennen, 2008)
Application to the SIR epidemic model (Frank Wang, 2010)