Phylogenetic Analysis

Analysis
Previous pages have laid out the taxonomic and morphological scope of our analysis. We will attempt to score as many of the published titanosaur species as possible for the 438 osteological characters we have selected from previous analyses (available here). We intend to score as many as possible species from first-hand observation. We hope that this approach will minimize the number of mis-scorings based on errors in the literature or difficulties interpreting figure and photographs, as well as provide opportunity to make alpha-level revision of relevant taxa and create novel characters.
Terminal taxa and outgroup taxa will be scored for the core characters to build a character-taxon data matrix MacClade 4 (Maddison & Maddison 2000). Outgroups to Titanosauria are found within Macronaria (Salgado et al. 1997; Wilson & Sereno 1998) and include Euhelopus, Brachiosaurus, and Camarasaurus. The final matrix will be examined and subjected to Safe Taxonomic Reduction (Wilkinson 1995) to remove redundant terminal taxa. The resultant character-taxon matrix will be evaluated in PAUP* (Swofford 2000) and NONA (Goloboff 1993). Strict consensus trees will be used to identify hypotheses of relationship common to the equally parsimonious source trees. The robustness of the cladistic hypothesis will be evaluated using decay analysis (Bremer 1994) and double-decay analysis (Wilkinson et al. 2000, 2003). The resultant topology will be compared to topologies suggested by previous analyses of Titanosauria and hypothetical topologies specific to evolutionary questions such as body size-specific clades (see below). Quantitative comparisons (e.g., Templeton test; Templeton 1983) between these alternate topologies and our most parsimonious topology will allow us to statistically evaluate specific evolutionary hypotheses.
Missing data is an important consideration in this analysis, and we attempt to limit its deleterious effects by our choice of terminal taxa, accurately distinguishing types of missing data in the matrix, and exploring its effects using data substitution methods. Our most complete species, Rapetosaurus krausei, could not be scored for 75 (17%) of the 440 characters. Other titanosaur species are more poorly known and will accrue higher levels of missing data. The high number of terminal taxa and the prevalence of missing data are likely to produce many most parsimonious trees and lower resolution (Huelsenbeck, 1991; Nixon & Wheeler 1992; Novacek 1992; Wilkinson 1995; Kearney & Clark 2003), although these are not always strictly correlated (Kearney 2002:table 1). Recent cladistic analyses of sauropods range between 44–63% missing data, but the number of most parsimonious trees ranges from 2–200,000:
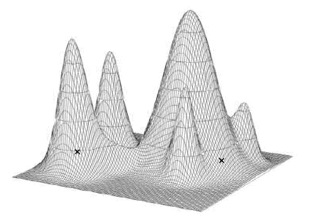
The analyses with the highest number of most parsimonious trees are those with the largest matrices, suggesting that effects of missing data are most pronounced in large data sets. Matrix size can be reduced by employing arbitrary “taxon cutoffs” (Rowe 1988) or “character cutoffs” (de Quieroz & Wimberger 1993). Culled taxa can then be “re-inserted” into the cladogram using synapomorphies discovered in analysis of more complete taxa (Grande & Bemis 1998; Wilson 2002). These measures equate missing data with uncertainty, but anatomical completeness is not an index for phylogenetic informativeness – a taxon or character with large amounts of missing data can be phylogenetically informative (Wilkinson 1995) and lack of resolution may indicate character conflicts (Kearney & Clark 2003). Although we agree that arbitrary completeness thresholds may remove important data from an analysis, not every specimen attributed to the ingroup can be included in an analysis. We will restrict our analysis to species that are well-diagnosed; that is, those taxa known from sufficient material to be robustly differentiated from other species. Although subjective, this criterion is not arbitrary; it will require detailed alpha-level information about each species and will establish a morphological threshold for terminal taxon selection. The species listed in Table 1 will be added to during the course of our study.
We will also profile our data matrix to examine the taxa and character types most affected by missing data. We will distinguish missing data entries (?) in our matrix from those in which information is polymorphic (P), unresolved homology (*), inapplicable (N), or inaccessible (X) (Grande & Bemis 1998). Missing entries will be tallied for each terminal taxon and character and separated by anatomical region. This type of profiling will allow us to try to bolster character coverage in a particular region or to preferentially include terminal taxa that preserve key anatomical regions.
We will attempt to identify nodes that may be susceptible to the effects of missing data using MERDA (Norell & Wheeler 2003). This method replicates analyses with missing data cells replaces by observed values, allowing the user to examine the universe of possible outcomes. The relative frequency of a particular clade in replicate trials yields an index of its robustness.
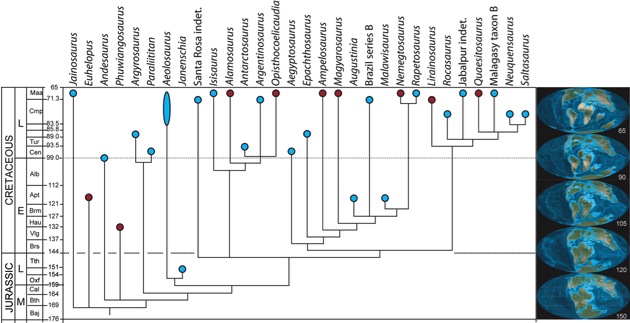
Calibrated phylogeny of titanosaur sauropods, based on the results of Curry Rogers (2005). Blue and red circles indicate Gondwanan and Laurasian species, respectively. Internode branches are vertically exaggerated for ease of reading. Paleocoastline reconstructions at right are from Ron Blakey, Northern Arizona University.

