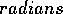Angular velocity is related to the rate of rotation, that is
the number of rotations per second. It is most convenient to
use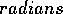 
to measure angles, because the angle in radians
of an arc of length 
is related to the radius of the arc by
For an entire circle, the angle subtendend by the circumfrence (360
) is
The units of angular velocity are r/s (radians per second). Angular velocity is a vector quantity. Clearly a rotating object (a bicycle wheel for example) has a plane of rotation and a sense of rotation. The vector angular velocity of a rotating object is, by convention, directed perpendicular to the plane of rotation and toward from the plane for clockwise rotation and away from the plane for counter-clockwise rotation. This is a right hand rule, that is curl the fingers of the right hand in the direction of rotation and the thumb points along the conventional angular momentum vector. Angular velocity is given the symbol
. We will most often consider motion in a plane, and it is convenient to eliminate the arrow indicating the vector.
Consider a rotating disk, the angle through which it rotates in a time
is
A piece of the disk a distance
from the axis of rotation will move along an arc a length
And the magnitude of the velocity of the piece of the object is
Angular acceleration is the rate of change of
. The basic description of angular motion directly parallels the description of linear motion which follows from Newton's calculus. The table shows the quantities of angular motion.
