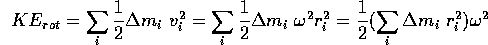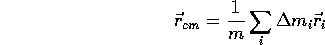Moment of Inertia



Next: The Parallel Axis
Up: Physics 125Fall
Previous: Angular Velocity and
The total  of an object is the sum of the
of an object is the sum of the  of each piece and is separated into rotational and translational
of each piece and is separated into rotational and translational
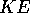 . We will first consider
an object with no translational
. We will first consider
an object with no translational 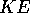 . The rotational
. The rotational 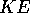 is then the total
is then the total 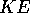 given by adding up
given by adding up 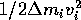 for each
little piece of mass
for each
little piece of mass  .
.
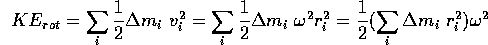
The quantity

is characteristic of the
mass distribution and is a measure of the rotational inertia. It is
called the moment of inertia,


The rotational

of an object is

Which is analagous to translational

.
The moment of inertia of an object depends on its mass, size, and
shape.

increases
as the mass is more concentrated toward the outside of the object.
Thus objects of equal masses and even equal radii can have different
moments of inertia. For a thin ring,

, and for a disk,

.
Integral
calculus can be used to find the moment of inertia of many objects.
The table below provides some results for objects of uniform density.
The mass of the object is

And the center of mass position is given by
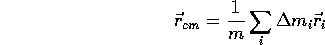
The distribution of mass of an object is partly characterized by these
so called moments:

,

, and

.
Fig 3 Moments of inertia for objects of several shapes calculated
about a specific axis. In all cases, the mass of the object is

Scott D. Dexter
Tue Dec 5 15:33:45 EST 1995
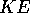 of an object is the sum of the
of an object is the sum of the 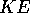 of each piece and is separated into rotational and translational
of each piece and is separated into rotational and translational
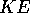 . We will first consider
an object with no translational
. We will first consider
an object with no translational 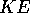 . The rotational
. The rotational 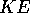 is then the total
is then the total 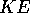 given by adding up
given by adding up 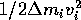 for each
little piece of mass
for each
little piece of mass  .
.