Idealized Dynamical Core Test Cases for Weather and Climate Models

Test of the Dynamical Core of General Circulation Models:
Short deterministic and long climate simulations

---

Professor Christiane Jablonowski (cjablono@umich.edu)

Weather Prediction modeling

Tests of the Dynamical Core

Workshops and DCMIP

DCMIP snapshots

Held-Suarez Test: The models GME, GM and IFS

Held-Suarez Test Results

Partners

  A few comments on weather prediction modeling

Weather prediction models or generally speaking atmospheric general circulation models are the discrete, numerical representatives of the underlying governing physical laws. The following two web sites provide first insight into the concepts of a weather prediction model and give some hints concerning its complex structures.

Numerical weather prediction models at the German Weather Services (DWD), Offenbach, Germany

Modelling and Prediction at the European Centre for Medium-Range Weather Forecasts (ECMWF), Reading, England

 

  Tests of the Dynamical Core of a General Circulation Model (GCM)

Atmospheric models consist of several components which describe the state of the atmosphere. Important model components are the dynamics package, the so-called dynamical core, and the physics package which strongly interacts with the dynamical core in a non-linear fashion. The dynamical core contains the large-scale adiabatic part of a model (the discretized equations of motion) and is explicitly resolved on the underlying grid, whereas the physics is characterized by diabatic, subgrid-scale processes. These physical processes such as radiation, clouds, friction and boundary layer interactions play an important role in the general circulation. However, their characterisic spatial scales are too small to be resoved on a typical GCM grid with grid spacings of order 50 km or wider. Therefore, the overall effects of the small-scale processes are estimated via so-called physical parameterizations. These are often derived empirically.

The interaction of the model components in a full GCM makes it difficult or even impossible to decide which phenomena are caused by which model component. Each attempt to gather information on a specific model component - so for example information on the dynamical core of a model - is influenced by the impact of the physical parameterizations. This difficulty is alleviated when testing the dynamical core in isolation. This can ve viewed as a 'unit test before coupling the dynamics to the physics parametrization suite. Dry dynamical core tests give valuable information about the characteristics of the numerical discretizations, such as the diffusive behavior, and are especially useful as a begugging tool during the model development phases. In addition, dynamical cores can be intercompared which provides information about the uncertainties in the numerical solutions.

Two groups of dynamical core tests need to be distinguished. First, dynamical cores can be tested with short deterministic test cases which typically cover a simulation period of about 10-30 days. Second, dynamical cores can be tested in a climate mode that assesses the statistics of the model simulations. These runs span a multi-year time period and are typically run with simple prescribed forcings (Rayleigh friction and Newtonian temperature relaxation) that replace the complex physics suite. Two such dry 'climate' forcings have been suggested in the literature. They are known as the Held-Suarez test and the Boer-Denis test which are briefly described below. We extended these dry test paradigms and developed a moist variant of the Held-Suarez test in Thatcher and Jablonowski (2016).

Deterministic Dynamical Core Tests

Short deterministic test cases for dynamical cores have become prominient over the last decade and our research group has played a paramount role in defining them. The key to their widespread use is that they need to be 'easy-to-implement'. Short dynamical core test cases start from prescribed initial conditions that are ideally provided in analytic form. The simulations are run in a 'forecast mode' for 10-30 day time periods and are either compared to analytic solutions (if available) or high-resolution reference solutions. Examples of dry dynamical core test cases are the Jablonowski-Williamson steady-state and baroclinic wave test (Jablonowski and Williamson, QJ 2006; Williamson et al., MWR 2009; Lauritzen et al., JAMES 2010), 3D advection, Rossby-Haurwitz waves, mountain-generated Rossby waves or gravity waves (Jablonowski et al. 2008, Ullrich and Jablonowski, JCP 2012). We also suggest a moist tropical cyclone test case in aqua-planet mode that can either be run in a full-physics or simple-physics setup (Reed and Jablonowski, JAMES 2012). These simulations are initialized with a weak axisymmetric vortex that is embedded into tropical environmental conditions (Reed and Jablonowski, MWR 2011). The vortex then evolves into a tropical cyclone over 10 simulation days. This collection and examples of the model simulations are provided in:

• Jablonowski, C. and D. L. Williamson (2006): A baroclinic instability test case for atmospheric model dynamical cores , Quart. J. Roy. Meteorol. Soc., Vol. 132, 2943-2975


• Jablonowski, C. and D. L. Williamson (2006b): A Baroclinic Wave Test Case for Dynamical Cores of General Circulation Models: Model Intercomparisons , NCAR Technical Note NCAR/TN-469+STR, Boulder, CO, 89 pp.


• Jablonowski, C., P. H. Lauritzen, R. Nair and M. Taylor (2008): Idealized test cases for the dynamical cores of Atmospheric General Circulation Models: A proposal for the NCAR ASP 2008 summer colloquium, May/29/2008, Technical Report


• Jablonowski, C., P. H. Lauritzen, M. A. Taylor and R. Nair (2008): An intercomparison of 10 atmospheric model dynamical cores, Presentation at AGU Fall Meeting, San Francisco, CA, USA, December 15-19, 2008


• Jablonowski, C., P. H. Lauritzen, R. Nair and M. Taylor (2009): A test suite for GCMs: An intercomparison of 10 atmospheric dynamical cores, Presentation at the Workshop on Solutions to Partial Differential Equations on the Sphere, Santa Fe, USA, April 27-30, 2009


• Williamson, D. L., J. Olson and C. Jablonowski (2009): Two dynamical core formulation flaws exposed by a baroclinic instability test case, Mon. Wea. Rev., Vol. 137, 790-796


• Lauritzen, P. H., C. Jablonowski, M. A. Taylor and R. D. Nair (2010): Rotated versions of the Jablonowski steady-state and baroclinic wave test cases: A dynamical core intercomparison, J. Adv. Model. Earth Syst., Vol. 2, Art. #15, 34 pp, Article Spotlight in Dec. 2009


• Reed, K. A. and C. Jablonowski (2011a): An Analytic Vortex Initialization Technique for Idealized Tropical Cyclone Studies in AGCMs, Mon. Wea. Rev., Vol. 139, 689-710


• Reed, K. A. and C. Jablonowski (2011b): Impact of physical parameterizations on idealized tropical cyclones in the Community Atmosphere Model, Geophys. Res. Lett., Vol. 38, L04805


• Reed, K. A. and C. Jablonowski (2011c): Assessing the Uncertainty of Tropical Cyclone Simulations in NCAR's Community Atmosphere Model, J. Adv. Model. Earth Syst., Vol. 3, Art. 2011MS000076, 16 pp.


• Reed, K. A. and C. Jablonowski (2012): Idealized tropical cyclone simulations of intermediate complexity: a test case for AGCMs, J. Adv. Model. Earth Syst., Vol. 4, M04001, doi:10.1029/2011MS000099


• Ullrich, P. A. and C. Jablonowski (2012): MCore: A Non-hydrostatic Atmospheric Dynamical Core Utilizing High-Order Finite-Volume Methods, J. Comput. Phys., Vol. 231, 5078-5108


• Kent, J., C. Jablonowski, J. P. Whitehead and R. B. Rood (2012), Downscale Cascades in Tracer Transport Test Cases, Geoscientific Model Development, Vol. 5, 1517-1530


• Ullrich, P. A., C. Jablonowski, J. Kent, P. H. Lauritzen, R. Nair, M. A. Taylor (2012): Dynamical Core Model Intercomparison Project (DCMIP) Test Case Document, Technical Report, version 1.7 from Jan/13/2013


• Jablonowski, C., P. A. Ullrich, J. Kent, K. A. Reed, M. A. Taylor, P. H. Lauritzen, and R. Nair (2012): The 2012 Dynamical Core Model Intercomparison Project (DCMIP), Presentation at AGU Fall Meeting, San Francisco, CA, USA, December 3-7, 2012


• Kent, J., P. A. Ullrich and C. Jablonowski (2014): Dynamical Core Model Intercomparison Project: Tracer Transport Test Cases, Quart. J. Roy. Meteorol. Soc., Vol. 140, 1279-1293


• Ullrich, P. A., T. Melvin, C. Jablonowski and A. Staniforth (2014): A proposed baroclinic wave test case for deep- and shallow-atmosphere dynamical cores, Quart. J. Roy. Meteorol. Soc., Vol. 140, 1590-1602


• Whitehead, J. P., C. Jablonowski, J. Kent and R. B. Rood (2015), Potential vorticity: Measuring consistency between GCM dynamical cores and tracer advection schemes, Quart. J. Roy. Meteorol. Soc., Vol. 141, 739-751


• Ullrich, P. A., K. A. Reed and C. Jablonowski (2015), Analytical initial conditions and an analysis of baroclinic instability waves in f- and beta-plane 3D channel models, Quart. J. Roy. Meteorol. Soc., Vol. 141, 2972-2988


• Hall, D. M., P. A. Ullrich, K. A. Reed, C. Jablonowski, R. D. Nair and H. M. Tufo (2016), Dynamical Core Model Intercomparison Project (DCMIP) Tracer Transport Test Results for CAM-SE, Quart. J. Roy. Meteorol. Soc., Vol. 142, 1672-1684, doi:10.1002/qj.2761


• Ullrich, P. A., C. Jablonowski, K. A. Reed, C. Zarzycki, P. H. Lauritzen, R. Nair, J. Kent and A. Verlet-Banide (2016): Dynamical Core Model Intercomparison Project (DCMIP2016) Test Case Document, Technical Report, version from June/10/2016


• Thatcher, D. R. and C. Jablonowski (2016), A moist aquaplanet variant of the Held-Suarez test for atmospheric model dynamical cores, Geosci. Model Dev., Vol. 9, 1263-1292


• Zarzycki, C. M., C. Jablonowski, J. Kent, P. H. Lauritzen, R. Nair, K. A. Reed, P. A. Ullrich, D. M. Hall, D. Dazlich, R. Heikes, C. Konor, D. Randall, X. Chen, L. Harris, M. Giorgetta, D. Reinert, C. Kühnlein, R. Walko, V. Lee, A. Qaddouri, M. Tanguay, H. Miura, T. Ohno, R. Yoshida, S.-H. Park, J. Klemp, and W. Skamarock (2019), DCMIP2016: The Splitting Supercell Test Case, Geosci. Model Dev., Vol. 12, 879–892


• Jablonowski, C., P. A. Ullrich, C. M. Zarzycki, K. A. Reed, J. Kent, P. H. Lauritzen and R. Nair (2018), Updated Results from the Dynamical Core Model Intercomparison Project (DCMIP-2016), presentation at the CESM Atmosphere Model Working Group (AMWG) Meeting, Boulder, CO, USA, February 12-14, 2018


• Jablonowski, C., P. A. Ullrich, C. M. Zarzycki, K. A. Reed, J. Kent, P. H. Lauritzen and R. Nair (2018), Analyzing Physics-Dynamics Coupling in an Ensemble of Simplified GCMs, presentation at the 3rd Workshop on Physics-Dynamics Coupling (PDC18), European Centre for Medium-Range Weather Forecasts (ECMWF), Reading, U.K., July 10-12, 2018


• Ferguson, J. O. and C. Jablonowski (2019), Assessing Adaptive Mesh Refinement (AMR) in a Forced Shallow-Water Model with Moisture, Mon. Wea. Rev., Vol. 147, 3673–3692 (Tests of a 'moist' 2D shallow water model)

Additional information is available on the following web pages that provide

• high-resolution reference solutions and the uncertainty estimates for the baroclinic wave test case (Jablonowski and Williamson, QJ 2006).
• an overview of our dynamical core research at the University of Michigan.
.

Held-Suarez Test

This test of the dynamical core has been designed by Isaac Held (GFDL, Princeton) and Max Suarez (NASA) who published the test method in 1994. The article is available online from AMS:
 Held, I. M. and M. J. Suarez (1994): A proposal for the intercomparison of the dynamical cores of atmospheric general circulation models, Bull. Am. Meteorol. Soc. 73, 1825-1830 .

The Held-Suarez test evaluates the dry dynamical core without any topography in a climate mode. 1200-day integrations are required that allow the assessment of climate statistics like the zonal-mean time-mean general ciculation and the Eddy fluxes. The basic idea behind the test method is to replace the complex physics package with simple forcing functions. These idealized forcings consist of a Newtonian temperature relaxation towards a prescribed thermal equilibrium temperature and Rayleigh friction for the wind at lower levels. Using these forcings a dynamical core can be tested on its own or can be compared with other dynamical cores because the dynamically induced circulation is no longer influenced by interactions with the physical parameterizations.

A variation of the Held-Suarez test has been developed by D. L. Williamson, J. G. Olson and B.A. Boville, NCAR, Boulder, USA, in 1998 and is here referenced as the Held-Suarez-Williamson test. Williamson et al. (1998) modified the Held-Suarez temperature forcing function in the upper atmosphere (above 100hPa) to test the model behavior in the stratosphere and mesosphere. This change becomes important when using vertical high resolution models since the Held-Suarez forcing provides an isothermal, stable temperature profile in the upper atmosphere which keeps the stratosphere and mesosphere passive.
The Held-Suarez-Williamson test method has been published in:
Williamson, D. L., J. G. Olson and B.A. Boville (1998), "A Comparison of semi-Lagrangian and Eulerian tropical climate simulations", Monthly Weather Review 126:1001-1012 .

Thatcher and Jablonowski: A moist variant of the Held-Suarez Test

We developed a moist extension of the Held-Suarez test which is described in the online article:
 Thatcher, D. R. and C. Jablonowski (2016): A moist aquaplanet variant of the Held-Suarez test for atmospheric model dynamical cores, Geosci. Model Dev., Vol. 9, 1263-1292 .

This moist idealized test case (MITC) was inspired by the Held–Suarez (HS) test and the simplified moist physics package described in Reed and Jablonowski (JAMES, 2012). This moist variant of the HS test sheds light on the nonlinear dynamics–physics moisture feedbacks without the complexity of full-physics parameterization packages. In particular, it adds simplified moist processes to the HS forcing to model large-scale condensation, boundary-layer mixing, and the exchange of latent and sensible heat between the atmospheric surface and an ocean-covered planet. In Thatcher and Jablonowski (2016) we demonstrate (via a variety of dynamical cores of the National Center for Atmospheric Research (NCAR)’s Community Atmosphere Model (CAM)) that the inclusion of the moist idealized physics package leads to climatic states that closely resemble aquaplanet simulations with complex physical parameterizations. This establishes that the MITC approach generates reasonable atmospheric circulations and can be used for a broad range of scientific investigations. In our paper we provide examples of two application areas. First, the test case reveals the characteristics of the physics–dynamics coupling technique and reproduces coupling issues seen in full-physics simulations. In particular, we show that sudden adjustments of the prognostic fields due to moist physics tendencies can trigger undesirable large-scale gravity waves, which can be remedied by a more gradual application of the physical forcing. Second, the moist idealized test case can be used to intercompare dynamical cores. These examples demonstrate the versatility of the MITC approach and we make further suggestions of other application areas. The new moist variant of the HS test can be considered a test case of intermediate complexity.

Boer-Denis Test

Another method to test the dry dynamical core in a 'climate mode' was introduced by Boer and Denis (1997). All details are provided in their article
Boer, G. J. and B. Denis, (1997), "Numerical convergence of the dynamics of a GCM", Clim. Dyn. 13:359-374 .

The Boer-Denis test is similar to the Held-Suarez test. The physics package is replaced with an idealized forcing mechanism. These forcing functions are based on two prescribed temperature and heating profiles as well as a friction term that slows down the wind at lower levels.

  Forum for Dynamical Core Test Cases:
     Workshops and the Dynamical Core Model Intercomparison Project (DCMIP)

Ideas for new dynamical core test cases and the results of model intercomparisons are discussed at the 'Partial Differential Equations on the Sphere (PDEs on the Sphere)' workshops that take place every 18-24 months. The list of the PDEs on the Sphere Workshops since 1998 can be found below. In addition, I am one of the founders of the 'Dynamical Core Model Intercomparison Project (DCMIP)' which is based on our experience with three summer schools. In 2008, we conducted a hands-on model intercomparison workshop and summer school at NCAR that focused on dry dynamical core tests (Jablonowski et al. 2008). In the summer of 2012, we conducted the DCMIP-2012 summer school with a focus on non-hydrostatic dynamical cores and their interactions with simplified moisture processes. In the summer of 2016, the DCMIP-2016 summer school put even more emphasis on the interaction between nonhydrostatic dynamical cores and simplified physics processes.

Links to the Dynamical Core Model Intercomparison Project (DCMIP) and Summer Schools:

• 2008 Colloquium on 'Numerical Techniques for Global Atmospheric Models', organized by Jablonowski, Lauritzen, Nair and Taylor, and hosted by NCAR's Advanced Study Program (ASP), Boulder, CO, June 2008


• 2012 DCMIP Summer School on Future-Generation Non-Hydrostatic Weather and Climate Models, organized by Jablonowski, Ullrich, Kent, Lauritzen, Nair and Taylor, and hosted by NCAR's Computational & Information Systems Laboratory (CISL), Boulder, CO, 7/30-8/10/2012


• 2016 DCMIP Summer School on Future-Generation Non-Hydrostatic Weather and Climate Models, organized by Ullrich, Jablonowski, Reed, Zarzycki, Lauritzen, Nair, and Kent, and hosted by NCAR's Computational & Information Systems Laboratory (CISL), Boulder, CO, 6/6-6/17/2016


• Joint World Climate Research Programme (WCRP) and DCMIP-2022 Summer School on Earth System Model Development: Dynamical cores and physics-dynamics coupling, organized by Lauritzen, P., P. Ullrich, C. Jablonowski, K. Reed, C. Zarzycki, A. Herrington, H. Morrison, M. Taylor , and hosted by NCAR's Climate and Global Dynamics Laboratory (CGD), Boulder, CO, 8/15-19/2022

The DCMIP test case suites:

• The DCMIP-2008 test case document: Jablonowski, C., P. H. Lauritzen, R. D. Nair and M. Taylor (2008): Idealized test cases for the dynamical cores of Atmospheric General Circulation Models: A proposal for the NCAR ASP 2008 summer colloquium, version from May/29/2008


• The DCMIP-2012 test case document: Ullrich, P. A., C. Jablonowski, J. Kent, P. H. Lauritzen, R. Nair, M. A. Taylor (2012): Dynamical Core Model Intercomparison Project (DCMIP) Test Case Document, version 1.7 from Jan/13/2013


• The DCMIP-2016 test case document: Ullrich, P. A., C. Jablonowski, K. A. Reed, C. Zarzycki, P. H. Lauritzen, R. Nair, J. Kent and A. Verlet-Banide (2016): Dynamical Core Model Intercomparison Project (DCMIP2016) Test Case Document, version from June/10/2016

PDEs on the Sphere Workshops

• Breckenridge, Colorado, USA, June 1996
• Gatlinburg, Tennessee, USA, Oak Ridge National Laboratory, April 1998
• San Francisco, California, Lawrence Livermore National Laboratory, November 1999
• Montreal, Quebec, Canada, Environment Canada, May 2001
• Toronto, Ontario, Canada, Fields Institute, August 2002
• Yokohama, Japan, Frontier Research Center for Global Change (FRCGC), July 2004
• Monterey, California, USA, Naval Research Laboratory, June 2006
• Exeter, United Kingdom, U.K. Met Office, September 2007
• Santa Fe, New Mexico, Los Alamos Natonal Laboratory, April 2009
• Potsdam, Germany, Alfred-Wegener Institute (AWI), August 2010
• Cambridge, U.K., Isaac Newton Institute for Mathematical Sciences, September 2012
• Boulder, Colorado, NCAR, April 2014
• Seoul, South Korea, KIAPS, October 2015
• Paris, France, Le Laboratoire de Météorologie Dynamique (LMD), April 2017
• Montreal, Canada, Environment and Climate Change Canada , April/May 2019
• Offenbach, Germany, German Weather Service, May/17-21/2021 virtual workshop

  Snapshots of dry dynamical core test cases and the DCMIP intercomparison from 2008

3D advection with prescribed winds:

Figure: Selected results of the dynamical core intercomparison project conducted during the 2008 NCAR ASP summer school. The names of the dynamical cores are specified in the headers. The figure shows a cross section of an advected slotted ellipse after 12 days that was transported up and down and around the sphere via an analytically prescribed 3D wind field. The initial condition and reference solution can be used to assess the characteristics of the advection schemes in the participating models denoted by the acronyms. The horizontal grid spacings are approximately 110 km with 60 levels in the vertical direction (vertical grid spacing is 250 m).

Baroclinic wave:

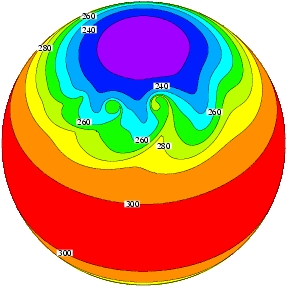
Figure: Surface pressure field at day 9 of the baroclinic instability test case simulated with 9 different dynamical cores. The tests starts with balanced initial conditions that are overlaid by a Gaussian hill perturbation. The grid imprint of the cubed-sphere and icosahedral grids can be seen in the Southern Hemisphere (GEOS-FVCUBE, GME, ICON, OLAM). Spectral ringing appears in CAM-EUL and HOMME. The baroclinic wave test is documented in Jablonowski and Williamson (QJ, 2006) and in the Jablonowski and Williamson NCAR Technical Report TN-469+STR (2006).

  Held-Suarez Test and Model Intercomparison: Models GME, GM and IFS

Overview of the models

The dynamical cores of three different general circulation models have been tested using the proposal of Held-Suarez. The models involved in this investigation are global weather prediction models that are or have been used operationally at the German Weather Center (DWD, Offenbach, Germany) and the European Centre for Medium-Range Weather Forecasts (ECMWF, Reading, England). The table below provides an overview of these GCMs and their numerical designs.
 
 

Numerical properties of the global weather prediction models GME Version 1.7 (DWD model), GM Version 1.15 (DWD model) and IFS cycle 18 (ECMWF model).

	GME (DWD)	GM (DWD)	IFS (ECMWF)
Model type	Grid point model	Spectral model	Spectral model
Grid	Spherical icosahedral grid	Gaussian grid	Reduced Gaussian grid
Horizontal discretization	finite differences, 2nd order	spectral triangular truncation	spectral triangular truncation
Horizontal resolution	ni=64 (approx. 110 km)	T106 (approx. 125 km)	T106 (approx. 125 km)
Vertical resolution	hybrid 19 levels	hybrid 19 levels	hybrid 31 levels
Model top	10 hPa	10 hPa	10 hPa
Prognostic variables (dry model)	zonal wind u meridional wind v temperature T surface pressure ps	relative vorticity horizontal divergence temperature T natural logarithm (ps)	relative vorticity horizontal divergence temperature T natural logarithm (ps)
Advection scheme	Eulerian	Eulerian	Semi-Lagrange
Time stepping scheme	semi-implicit 3-time-level	semi-implicit 3-time-level	semi-implicit 2-time-level
Time step	400 s	900 s	2700 s
Diffusion	linear, 4th order	linear, 4th order	linear, 4th order

Comparison of the grids

An important - and most obvious - difference between the three models is the different underlying grid structure. In contrast to the two spectral models GM (DWD) and IFS (ECMWF) that use a quasi-regular Gaussian or reduced Gaussian grid, the DWD model GME is based on an irregular, spherical icosahedral grid. This grid structure has been chosen in order to avoid the so-called 'pole problem' (convergence of the meridians near the poles) that is present in regular latitude-longitude grids.
The design of the spherical icosahedral grid is demonstrated below. An icosahedron is a geometric construct that consists of 20 identical triangles which touch the surrounding sphere at 12 points. This grid represents an icosahedral grid at the resolution ni=1 and can now be continuously refined. Each refinement step divides each side of the icosahedral triangles into two, so that the number of refinements 'ni' can be used to indicate the grid resolution. The following figures illustrate the structure of the icosahedral grid at the resolution ni=1, ni=2 and ni=4 (from left to right).

In contrast, a Gaussian grid represents a quasi regular latitude-longitude grid and its principle grid structure is shown in the figure below.

  Held-Suarez test results: A comparison of the dynamical cores of GME, GM and IFS

Convergence analysis: The DWD model GME

• Test design
• GME convergence analysis with respect to the horizontal resolution
• Zonal wind
• Eddy heat flux
• Eddy momentum flux
• Eddy kinetic energy

Dynamical core intercomparison: The models GME, GM and IFS

• Test design
• Comparison of the three dynamical cores
• Zonal wind
• Temperature
• Eddy heat flux
• Eddy momentum flux
• Eddy kinetic energy

Vertical high resolution experiment with the ECMWF model IFS

In January 1998 the dynamical core of the ECMWF model IFS at T63 resolution has been tested with an increased vertical resolution. Instead of the operational 31 vertical levels 50 model levels have been used to improve the vertical resolution especially in the upper atmosphere (stratosphere and lower mesosphere which lie between 11 km - approximately 50 km). The model top has been set to a pressure level of 0.1 hPa. This approach has led to interesting and new model results that are still under investigation.
The vertical high resolution dynamical core test produced a long-term oscillation in the tropical upper atmosphere that resembles the well known meteorological phenomenon of a QBO (quasi-biennial oscillation). The QBO phenomenon is characterized by a change of the major zonal wind regime in the equatorial region of the stratosphere. In nature, it is observed that easterly and westerly wind components change in a specific way approximately every 22-30 months. These wave structures have been well-met by the dynamical core test, but the model simulations are dominated by a longer time period.
This QBO-like oscillation of the IFS dynamical core has been an impressive and unexpected result. The underlying figure shows a cross section of the mean zonal wind along the equator and demonstrates the change in the zonal wind characteristics over a time period of 4800 days (approx. 13 years). Units are m/s.

Snapshots

The dynamical core tests at DWD have been initialized with artificial initial conditions and generate during the first 200-250 days of the long-term simulations a fully developed global circulation. The following snapshots provide insight into the beginning circulation on day 70. The underlying figures show the GME and GM surface pressure fields and the GME and GM temperature fields near the surface. In addition, the GME vertical velocity field demonstrates the different updraft and downdraft regions at 500hPa.
As far as the model GME is concerned it becomes obvious that the whole circulation is dominated by a wave number 5 structure which is connected to the icosahedral grid. This wave number 5 signal vanishes after model day 130 when baroclinic instability processes break the symmetry of the data.
Compare these images to those produced by I. Held, one of the authors of the dynamical core test method. He presents a snapshot of the temperature field (lower panel) and vertical motion (upper panel) in the lower troposphere (from the idealized atmospheric model (at 'T106' resolution) described in "A Proposal for the Intercomparison of the Dynamical Cores of Atmospheric General Circulation Models").

  Collaborators and Partners

University of Michigan alumni
Collaborators: Paul A. Ullrich (UC Davis), Kevin Reed (Stony Brook University), James Kent (U.K. Met Office, U.K.), Colin Zarzycki (Penn State University)

National Center for Atmospheric Research (NCAR), Boulder, CO, USA
Collaborators: David L. Williamson, Peter H. Lauritzen, Ram D. Nair

Sandia National Laboratories (SNL), Albuquerque, NM, USA
Collaborator: Mark A. Taylor