Geologists divide the Earth into three spherical zones. There is an inner zone that is mostly metallic. The diameter of this core is roughly half that of the entire earth. Most of the rest of the Earth is a rocky mantle, covered by a relatively thin crust. We have a very limited amount of direct information about the composition of the core and mantle, but there is a great deal of indirect information about these unseen layers. Most of this information is derived from ``listening'' to earthquakes with the help of instruments known as seismometers.
Above the crust of the Earth are the oceans and the earth's atmosphere. These are the regions of the Earth important to us, but they make up a tiny fraction of the mass of the whole earth. If we add all the mass in the oceans and polar caps, and throw in the atmosphere, the result is less than 6% of the mass of the earth's crust. And the crust is about 0.4% of the mass of the earth itself! Nevertheless, we will have to look rather closely at the chemistry of this trace amount of matter within which we live, because it will give important clues to the formation and history of the earth.
We can get a hint that the Earth can't be made up just of rocky materials from its mean density---the quotient of its mass by its volume. This density is about 5.5 times that of water. Now if we compare this figure with the densities of rocks, there is a considerable discrepancy. Rocks rarely have densities much more than 3 times that of water. We will give a few more precise figures later, but for the present, we ask how an Earth could be nearly twice the density of typical rocks. The most likely explanation is a core made of iron or a similar metal.
Certain rocks known as meteorites fall from the sky. Much of our current ideas about the composition of the planets comes from the study of these meteorites. Most meteorites are rocky in composition with small admixtures of dense metal inclusions. Others are almost entirely metallic in composition, with densities of the order of 8 times that of water. A few meteorites have comparable fractions of both metal and rock. The metal in these meteorites is typically quite high grade. If you cut the meteorite with a diamond saw, you can polish the face until it will reflect like a mirror. We shall often refer to this metal as `iron,' even though it is strictly a nickel-iron alloy.
Geologists have long believed these rocks came from one or more planets that had an iron cores and a rocky mantles, but were broken up somehow. It is interesting that astronomers resisted this notion for a long time. Even some rather recent textbooks written by astronomers soft-pedal the notion of meteorite parent bodies. But the Earth is the special province of the geologist, and only peripherally belongs to the astronomer. So these geologists have argued rather early on that the earth's core is probably made of material similar to the iron in meteorites. If some long destroyed parent body could have an iron core, why not the earth? Because the density of iron is much higher than that of rock, it is natural to think it would sink to form a core.
The earth's mantle is thought to be composed of rocky material that is, again, similar to that found in many meteorites. A few samples of the upper mantle come to us in pipes known as diatremes, and in regions where faults in the crust must have allowed extrusions of deeper rock. These materials, as well as the analyses of seismic waves are entirely consistent with a mantle composition similar to that of stony meteorites.
While the earth's core and mantle are each roughly 3000 km thick, the crust is as thin as 5 km, and rarely thicker than 20 km. The composition of this crust is considerably more complicated than we think the core or mantle to be. We shall discuss the origin of this complexity in due time. The crust of the Earth is pushed about by forces internal to the earth, giving rise to continental drift. A more technical phrase describing these motions of crustal fragments is plate tectonics.
The earth's Moon is unusual among planetary satellites. Basically, it's big. While there are satellites of the giant planets that are even bigger than our Moon, they are not bigger relative to these planets.
As a result of the space program, we know an enormous amount about the Moon and its structure. When I began to study astronomy in the late 1950's, we didn't even have a very precise notion of the Moon's mass. Now we know the mass of the Moon quite accurately, and we even know of irregularities in its distribution of mass. For example, irregularities in the motions of space vehicles have indicated concentrations of masses that correspond roughly to the regions called maria. Maria are the darker regions that can be seen on the face of the moon, even with the naked eye. The mascons were discovered by the early Lunar Orbiters in the missions prior to Apollo.
The Moon's bulk mass and density are about the same as that of rocks of the earth's upper mantle. Extensive analyses of moon rocks have told us that their overall composition resembles our estimates for the upper mantle. There are important differences. Lunar rocks are dryer, that is, they contain less water or other volatile substances. They also have a higher content of reduced, or metallic iron than mantle rocks. There are highly significant differences in the distribution of rock types in the crust of the Moon and the Earth that will lead us to infer very different histories for the formation of these surficial regions. It will be easier for us to be specific after we have had a chance to review rocks and minerals in a later chapter.
Mercury is the innermost planet of the solar system. It is less massive than the Earth or Venus, but 4.49 times the mass of the Moon. In size, Mercury is only a little bigger than the Moon. Its radius is 1.403 times the lunar radius. Now since volume depends on the cube of the radius, we might expect Mercury to have a mass of 1.403 cubed, or 2.76 times that of the Moon. Instead, the correct figure is 4.49. The obvious conclusion is that Mercury is made of much denser material than the Moon. It is easy to calculate from the figures here, that Mercury is 1.63 times more dense than the Moon.
We think Mercury has a relatively high density because of its iron core. This core is larger, relative to the size of the planet, than the cores of the Earth or Venus.
One aspect of the comparative densities of the planets needs to be discussed at this point. Gravity squeezes even solids when pressures get as large as they can be in planetary interiors. This means if we want to compare the materials from which the planets were originally formed, we have to allow somehow for this squeezing. The task is not easy, because we don't know for certain what it is that's being squeezed! But we can certainly make some reasonable estimates. We have already mentioned using the composition of meteorites. A reasonable guess for the squeezing properties---compressibilities---of the earth's material is that it is about the same as that of stony and iron meteorites.
Table 3-1
Terrestrial Planets and Minerals
Planet Distance from Density Decompressed
Sun (AU) gm/cm^3 density gm/cm^3
Mercury 0.39 5.43 5.3
Venus 0.72 5.24 3.9--4.7
Earth 1.00 5.52 4.0--4.5
Moon - 3.34 3.3
Mars 1.52 3.94 3.7--3.8
------------------------------------------
granite 2.6--2.8
basalt 2.4--3.1
kamacite 7.8
taenite 8.2
Estimated decompressed densities are shown in Table 3-1. We can see that the biggest changes are for the Earth and Venus---the larger pair of the four terrestrial planets. The smaller planets, Mercury and Mars, and the Moon are not squeezed much. But the table shows a remarkable trend of the decompressed densities. They decrease steadily from Mercury through Mars. Indeed, if we were to tack on the outer or Jovian planets, we would see that all have much lower densities still.
In the lower part of table 3-1 we give the densities of two common rock types, and the metallic minerals, taenite and kamacite. The latter minerals are often described as nickel-iron alloys---they are the major minerals of the iron meteorites. It is readily seen that any of the decompressed densities of the planets of the upper part of the table are bracketed by the materials in the lower part. We can therefore make a general inference from the densities alone.
We may simply assume that the ratio of iron to rock in the terrestrial planets decreases with distance from the sun. This density decrease should be a significant clue to the way in which these planets formed. We will return to this concept, and the remarkable American scientist Harold Urey, whose brilliant developments revolutionized the field of planetary formation (See Lecture 22).
Our considerations, based on densities and on the pieces of interplanetary debris known as meteorites lead us to quite different conclusions about the bulk composition of the Moon and Mercury. This may be surprising, in view of the similarity of their surfaces. Nevertheless, we may conclude that Mercury has a dominant metal core, while the Moon has a small core, or possibly no core at all. This structural difference reflects the very different histories of the two bodies.
One might expect the properties of Venus and Mars to bracket those of the earth. This is not really the case. The Earth is more massive, and larger than both planets, although Venus is nearly as large as the earth. Mars is about half the size of the earth, and as we can see from its density (table 3-1), it is mostly rock and little iron.
Venus is the closest planet to the earth, and most like it in size and mass. For many years the surface of Venus was hidden by the thick atmosphere. Of the four terrestrial planets, Venus has by far the most atmosphere. At the surface of the planet, the gas pressure is about 90 times that of the earth's atmosphere. The chemistry of the atmosphere is quite different from ours, though. Venus's atmosphere is mostly CO2 gas. There is about 3% N2, and only trace quantities of other gases. This is not unlike the composition of the atmosphere of Mars, but the pressure of the latter is slightly less than 0.01 Earth atmospheres.
As far as gas goes, there is essentially none on Mercury, lots on Venus, enough (for humans!) on earth, and piddling amounts on Mars. This gas nevertheless presents a challenge to our understanding of the chemical evolution of the planets. We may understand the history of this gas even less well than the much more massive rocky and metal phases of these planets, but when the time comes we shall consider this difficult problem.
Models of the interior of Venus pretty well parallel those of the earth, just scaled down a little. It's metal to rock ratio may be assumed to be the same as ours. The surface of Venus is quite different, of course. At the bottom of its thick atmosphere, the temperature, about 730 Kelvin, is more than high enough to melt lead (m.p. 601K). From numerous investigations from spacecraft, we know a good deal about the surface of this planet. Russian missions to Venus included landers that sent back a few pictures of rock-strewn surfaces. Radar from orbiters has allowed much of the surface to be mapped---we have ``pictures'' of Venus not unlike those available for Mars.
While the bulk properties of Venus and the Earth may be similar, the surfaces could not be more different. The Venusian surface temperature is above the so-called critical temperature of water, that is, the temperature at which water can only exist as a gas. And there is no water to speak of in the atmosphere of the planet either. Venus is not a particularly pleasant place to think about visiting.
Mars, on the other hand is not so disagreeable. A typical place on its surface is cold, but no colder than some places on the earth. Mars is certainly more likely to be explored in a manned space mission than Venus.
From its bulk properties---its size and density---it is not unreasonable to regard Mars as some kind of transition object, from the innermost planets to the very different giant or Jovian planets that lie considerably further from the sun. We might include among those transition objects the many smaller minor planets or asteroids.
It is useful to review at this point the scale of the distances of the planets from the sun. There is a simple algorithm that will give approximate distances known as Titius-Bode's law after two German astronomers of the late sixteenth century.
One way to express the algorithm of Titius-Bode's law is as follows. Write down a string of 4's, and beneath the fours write the sequence 0, 3, 6, 12, 24, 48, 96, 192. Add these numbers, and divide them by 10. These numbers are worked out in table 3-2. The actual distances from the sun are also shown. These distances are given in units of the earth--sun distance, called the astronomical unit or AU.
Table 3-2
The Titius-Bode Law
Planet 4 Add Sum/10 Actual dist (AU)
Mercury 4 0 0.4 0.39
Venus 4 3 0.7 0.72
Earth 4 6 1.0 1.00
Mars 4 12 1.6 1.52
asteroids 4 24 2.8 --
Jupiter 4 48 5.2 5.20
Saturn 4 96 10.0 9.54
Uranus 4 192 19.6 19.18
Neptune 4 384 38.8 30.06
Pluto 4 768 77.2 39.44
The Titius-Bode law is not a law at all---in the sense of Newton's laws or the laws of quantum mechanics. It may be best to think of it as only a mnemonic, even though a good deal of theoretical work has been done attempting to ``explain'' it. The law predicts that there should be something between Mars and Jupiter. Eventually, the asteroids or minor planets were found to occupy a ``belt'' roughly between 2.2 and 3.2 astronomical units from the sun.
The four terrestrial planets, Mercury, Venus, earth, and Mars are all relatively close together as planets go. The mean separations of Mercury and Mars is just a little over one AU. So the average separations of these four planets is only about 0.4 AU. On the other hand, the mean distance to the asteroid belt from Mars is about 1.5 AU. In other words, the asteroids are rather far away from the inner planets, and it is not difficult to imagine a rather different history for them.
There isn't much material in these asteroids. The largest, Ceres, is only about a quarter the size of the Moon. All together, the mass of the asteroids is thought to be less than 1% of the Moon's mass. On the other hand, there are a lot of little asteroids, and we can tell from the light reflected from their surfaces that they must vary in composition.
Our best guesses are that the asteroids are mostly rocky objects. However, if we are going to explain the iron of meteorites as originating in this belt, some asteroids must have been large enough to form cores. This is a reasonably involved question, since the ability to form a metallic core depends not only on the size of the body but also on the availability of heat sources to melt it. There are two main sources of heat that have been considered in this context, energy from the decay of radioactive materials, and gravity. It will be necessary for us to consider these heat sources in some detail.
We can see from table 3-2 that the distance between Mars and Jupiter is about twice the distance from the sun to Mars. Putting this another way, Jupiter is a good distance beyond Mars, and we might expect on this account alone, that it might be quite different in nature from the inner planets. It certainly is.
Jupiter dominates the planetary system by virtue of its mass. The planet is 318 times the mass of the Earth and 3.3 times the mass of the next largest planet, Saturn. It is well known that the orbits of the asteroids are strongly influenced by Jupiter's gravity. And there has long been speculation that a major planet could not have formed at the distance predicted by the Titius-Bode law because of perturbations from Jupiter.
The Jovian planets have a variety of satellite systems as well as rings. Prior to the space program, only Saturn was known to have rings. We now know that all Jovian planets have rings, although none as spectacular as those of Saturn. Unfortunately, we shall not have time to treat these highly interesting bodies in great detail. Their compositions mostly span the gamut from icy to rocky, and we shall already have dealt with this general topic in connection with the planets.
With the planet Jupiter, we encounter two more divisions of the materials that formed the planets---ice, or ices. Jupiter's density is 1.33, much too low to be dominated by any kind of rocky material. The ices that we speak of are frozen gases, predominantly water but with some ammonia (NH3), carbon dioxide (CO2), and trace species.
Actually, we think that Jupiter and Saturn have compositions not very different from that of the sun---mostly hydrogen and helium. So we shall add a fourth and final composition to our rough characterization of cosmic materials, the SAD. By definition, the SAD means the solar composition, primarily hydrogen and helium, with all other elements amounting to only 2% by mass.
All four planets are thought to have rocky cores, with some admixture of metal. In the case of the outer two these cores are more significant than for the inner two. All four Jovian planets have substantial magnetic fields, so their cores must be composed of material capable of conducting electricity.
Within substantial distance between Mars and Jupiter some significant change must have taken place when the planets were forming to explain the very great differences in the natures of the terrestrial and Jovian planets. We shall deal with this problem in later lectures, but we may look ahead briefly. We believe that in its earliest times, the planetary system was a flattened mixture of gas and dust which has been called the solar nebula. Within some 3 to 4 AU, the temperature was too high for water to freeze. The water remained mostly in the gaseous phase, and was swept away by violent winds from the young sun. Beyond this distance, recently called the snow line water froze, making snowballs around which the giant planets formed.
Pluto is rather small and curious. It is difficult to know how fits into the general scheme of planet formation. Fortunately, because it is so small, we may pass it by on a first consideration of the chemistry of the solar system.
Of the nine planets, only the innermost two, Mercury and Venus are without satellites. The Earth has the familiar Moon, while Mars has two rather small satellites.
The giant planets are surrounded by a very complicated system of orbiting bodies. The spectacular rings of Saturn have more mundane counterparts that surround Jupiter, Uranus, and Neptune. The ring systems about the latter three planets were unknown until the advent of the space program. Jupiter's ring system was discovered by the Voyager mission in 1979. Rings about the outer giant planets were discovered by ground based observations, and later confirmed by Voyager.
When it comes to the satellites of the major planets, there is a great deal of material to study. One of the Jovian satellites, Ganymede, and one of the Saturnian ones, Titan, are actually larger than the planet Mercury. Another Jovian satellite, Callisto, is only a bit smaller than Mercury. These are giant systems, and a great deal of attention has been paid to them.
The so-called Galilean satellites of Jupiter, Io, Europa, Ganymede, and Callisto, were discovered by Galileo (1564--1642). The objects were among the paroxysm of discoveries that followed his first application of a telescope to problems of astronomy. Galileo was incredibly gifted. It may be recalled that he did not invent the telescope, but having heard of its invention, immediately set out to construct one. Galileo's discoveries got him into trouble with officials of the Catholic Church. It is a fascinating story. We will have a little more to say about it in Lecture 8.
Galileo suggested that the moons he discovered about Jupiter were a miniature solar system, similar to the one suggested by Copernicus. This was a profound notion, still of value today, and not only because the Galilean satellites circle their parent body just as the planets do. For example, the densities of the Galilean satellites decrease from the innermost---from 3.57 gm/cm3 at Io to 1.86 gm/cm3 at Callisto. Planetary scientists have suggested that this density decline might occur for reasons similar to the density decrease of the planets themselves, from Mercury through the Jovian planets.
The densities of these giant Jovian satellites give us immediate insight into their chemistry. Io is slightly more dense than the earth's Moon (3.30 gm/cm3). We have already concluded that the Moon is composed primarily of rocky material, similar in nature to the earth's mantle. Clearly, the composition of Io must be similar. Just why Io is even more dense than the earth's Moon is a fascinating question. It may be related to the extraordinary activity that takes place on the body---volcanism and outgassing.
Io's ``geological'' activity may exceed that of the earth. Volcanic mountains and lava flows resurface the satellite at an estimated rate of one meter per 1,000 years. An estimate for erosional rates on the Earth is about 0.1 meter per 1000 years. Major changes of the earth's surface, such as the ``drift'' of the continents or carving to major canyons take some 100,000 years. Io may have been resurfaced as many as ten times during this period.
Telescopic observations of Io had indicated to astronomers that this was a most unusual body, but it was not until the Voyager missions in 1979 that we knew for sure just how strange it was. Interestingly, theoretical calculations by the American planetary physicists had predicted that Io's surface would be melted as a result of tidal forces between the satellite and Jupiter. The authors of this work, Peale, Cassen, and Reynolds had the unusual experience of having their theory confirmed---in spades---the same year their paper was published.
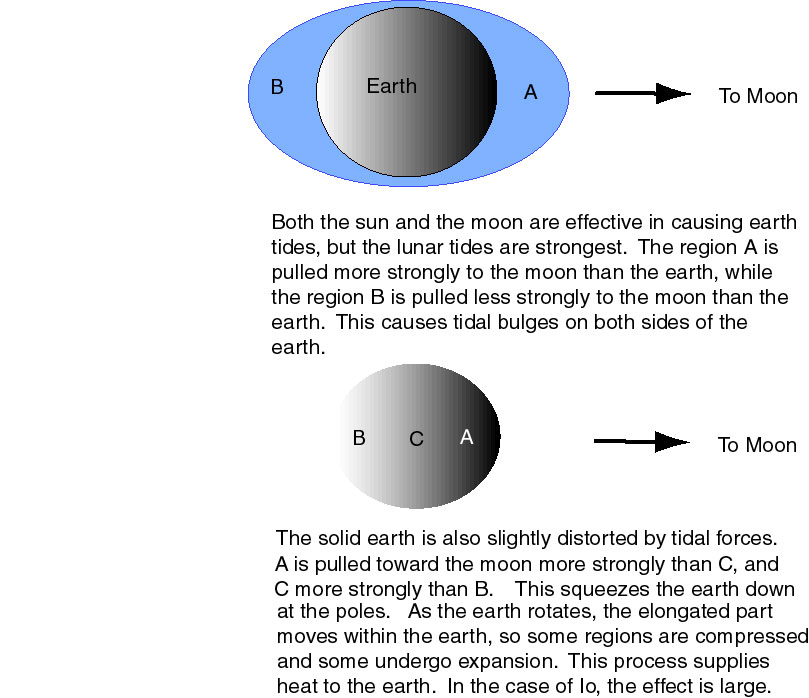
The basic theory of Peale et al. was that Io would be subject to similar forces to those that act between the Earth and Moon to raise the familiar oceanic tides. Less spectacular body tides occur on the Moon and the body of the earth, slightly changing their shape. The tidal forces are not constant, so the material gets squeezed and can then relax. This squeezing and unsqueezing deposits heat in the bodies, and this heat can be the cause of volcanic activity.
Figure 3-1: Tidal Forces. The blue areas in the upper part of the figure, represent the oceans (highly exagerated), which cover most of the earth. The oceans are not indicated in the lower part of the figure.

It is possible, but by no means certain, that the geological activity has boiled off enough of the volatile content of Io so that it is even denser than the Moon. This is no small feat, because we know that the Moon is a very dry body already. In this chapter where we have simplified the chemistry of the solar system to three basic ingredients, metal, rock, and ices, in decreasing order of density. Io must be mostly rock. As we move outward, to Europa, Ganymede, and Callisto, the fraction of rock to ice must steadily decrease. Callisto is still too dense to be entirely ice, and models show a rocky core about halfway to the center of this satellite.
Saturn's giant moon Titan has a density nearly the same as that of Callisto, so its structure must be just about the same---a rocky core and an ice mantle. Interestingly, the surface of Titan is enclosed in a nitrogen-rich atmosphere. Indeed, this satellite is the only one in the solar system with a substantial atmosphere. Why should this be so? Perhaps it is just a matter of the temperature.
We shall not dwell here on the myriad minor satellites of the Jovian planets. They are fascinating in a number of ways, but like the rings, their relationship to the overall chemistry of the solar system is probably minor. We cannot rule out that some significant clue remains hidden in the composition of these objects, but for the present, we must move on.
Comets have been known since ancient times. They appear as bright streaks of light in the sky, that move with respect to the stars. Most comets have a bright head, and a tail that may be several tenths of an astronomical unit in length. The known ones have orbits that take them to the inner solar system, where interaction with sunlight causes their often striking luminous features. Modern electric lighting, especially in cities, makes the night sky bright so comets appear relatively fainter than they would 100 or more years ago.
Some comets have orbits that cause them to return periodically to the inner solar system. The most famous of these is Halley's Comet. This object made spectacular appearances in Mark Twain's time, but was something of a dud when it most recently neared the sun in 1986. Our skies were too bright, and the comet itself may have mostly burned out. We know this happens to periodic comets because meteor showers or shooting stars are seen on nights when the Earth intersects orbits of old comets. When these old comets break up, their debris spreads out along their orbits, so that when the Earth passes through the orbit, pieces of the broken-up comet fall as shooting stars.
The comets are primarily icy bodies. Sunlight causes the ices to boil off, and luminesce. Most comets are located very far from the sun. There are two reservoirs, one only a little beyond Pluto and a second one at the limits of the solar system. The furthest reservoir is called the Oort Cloud, after a Dutch astronomer who first postulated it. The inner cloud is also named after a Dutch astronomer who spent most of his career in the United States. It is called the Kuiper belt.
The names reveal what we believe the geometry of these clouds to be. The Oort cloud is spherical, while the Kuiper belt is flattened, and in the plane of the solar system. In both cases, gravitational perturbations may cause a comet to approach the sun, allowing it to be observed from the earth. In the case of the Oort cloud, passing stars are believed responsible for the perturbations.
Kuiper belt comets feel significant gravitational pulls from the planets themselves, especially Jupiter. Accumulated perturbations over many-many orbital cycles may dislodge a comet from its position in the belt and cause it to enter the inner solar system. Once set on such a path, the comet may become periodic like the famous Halley's comet, and return after a fixed number of years. The new orbit would take the comet from the inner solar system, and back out to the Kuiper belt.
We would like very much to have a piece of a comet that we could analyze in our laboratories. There are a variety of reasons for thinking this material might reflect most closely the composition of the original solar nebula. This composition, of course, would be the starting point for any attempt to make models of the structure and history of the solar system itself. So keenly have researchers sought this composition, that others have facetiously referred to it as the Holy Grail.
Surely, we know a lot about the materials that comets are made of. Astronomers have observed the spectra of comets and identified various atoms and molecules. During the most recent Halley approach, spacecraft flew near the comet and made numerous observations. Unfortunately, no samples were returned to earth, so that what we learned is much less detailed than we would like.
The big problem with the bulk composition of comets is that we do not know their mass.
Newton's laws of gravity allow you to tell the mass of the body that is being orbited very precisely. So planetary motions tell us the mass of the sun. Similarly, the motions of satellites tell the mass of the parent planets. Prior to the space program, we only had an estimate of the Moon's mass from studies of the three body problem---the sun, the earth, and the Moon. This is the problem Newton said made his head ache. By modern times, the Moon's mass was known to somewhat more than three significant figures.
The Moon is sufficiently massive to interact rather strongly with the earth. Minor bodies of the solar system are much less massive, and their paths are determined primarily by the sun and nearby major planets.
We know relatively little about the masses of the asteroids, and consequently, we can only estimate their densities by assuming they are mostly rocky in nature. If we assume that we know the density of an asteroid, we can estimate its mass once its volume is known.
Some information on the sizes of asteroids is available. We know how bright they are, and we can make reasonable estimates of their reflectivities. Generally, their reflected light is consistent with the light that would be reflected from one kind of meteorite or another. Combining this information with their distances, and the energy they receive from the sun, we can tell how big they must be to have the brightnesses we observe. For a very few asteroids, we can also determine their sizes by making measurements as they pass in front of stars. Crudely speaking, the larger the asteroid, the longer time it will dim the light of a star.
When it comes to comets, it is very difficult to determine even the size of the solid nuclei. Unlike the asteroids, comets are surrounded by extensive gaseous material that conceals their central regions. The flyby missions to Comet Halley in 1986 did see a murky, potato- shaped nucleus about 15 x 8 km in cross section. Estimates of the density, however, had to be made from the measured gas/dust ratios ejected by the comet's activity, which was induced by the sunlight.
It turns out that comets are subject to ``non-gravitational forces'' due to jets of material coming from the nuclei. It is possible to ask how massive the comets must be in order to have their orbits affected by these jets. This gives one of the better estimates of the mass of Halley's Comet, about 1017 gm. Density estimates for the nucleus, then range from 0.1 to 0.5 gm/cm3---uncertain by a factor of five!
So for comets, we cannot use densities as an indication of the percentage of rock to ice, but perhaps an equally good idea of this can be obtained from the material that was ejected. The latter was thoroughly sampled. Dust to gas ratios in the ejecta fall in the range of 1/2 to 1/5. If we identify the dust with rocky material, and the gas with (mostly) vaporized ice, we see that comets have a higher percentage of ices than the outer planets or satellites. This is consistent with the notion that comets may be the most sun-like in composition of all bodies in orbit about the sun.
We have simplified the composition of materials by only considering four categories of matter---metals, rock, ices, and the solar composition, or SAD. We find the inner or terrestrial planets consist of metals and rock, with the metal/rock ratio diminishing from Mercury through Mars and the asteroids. The Jovian planets consist of small portions of metal and rock, ices, and substantial amounts of hydrogen and helium. Jupiter and Saturn may have compositions rather closely resembling the SAD. The densities of the planets give crude indications of what their compositions must be. We do not know the masses of many of the minor bodies of the solar system, and therefore do not know their densities. This situation applies to many satellites, to asteroids, and to comets. For these bodies, we may get some information about the chemistry of surficial matter, or in the case of comets, from material that has boiled off the surface.
We shall begin our survey with the universe itself. Perhaps the reader will find this an audacious, if not impudent notion. Isn't the universe the domain of philosophy if not religion? There is a way out of this difficulty.
The way was shown many years ago to the great pioneer Galileo Galilei by Cardinal Bellarmino (1542--1621). Galileo wanted badly to convince the world that the Earth was not at the center of what was then thought to be the universe---what we now call the solar system. Copernicus (1473--1543) had proposed, and Galileo firmly believed, that the sun was central. However, this idea was not popular with the power centers of Rome, and Bellarmino advised Galileo to take a different approach. He suggested that Galileo treat the notion of a heliocentric universe as a hypothesis, and not as something that was necessarily ``true'' in some fundamental sense. Galileo might have saved himself considerable grief if he had heeded this advice.
A modern name for what Bellarmino called `hypothesis' is model. Models are usually ideas that are thought to have approximate reality, but are not expected to have the full complexity of natural objects. Astronomers make model planets, model stars, and model universes. The models are scaled in such a way that the mind is not overwhelmed by the vastness of the distances and times.
If the notion of the universe as a whole seems formidable, then think about a model of it. Our model universe may be pictured as a large volume of space. For many purposes it is permissible to think of it as a big sphere, and we may scale the radius of the sphere down in our model until we can think of ourselves viewing the whole thing from the outside.
The sphere that may serve as our model universe will not have all the same properties as a cloud of gas such as a star. But many properties will be similar. In some ways our model universe will be similar to an exploding star. It may be helpful to think of models, and for the present, not to worry too much about the ``real'' universe.
People who work with models of the universe, cosmologists, may believe sincerely that their models are realistic. That's OK, perhaps they are. We can adopt that attitude too, if we want. If this notion is a bit too heavy, we can always say to ourselves, we are just considering models.
The devil is in the details. Cosmologists have a variety of ideas about how the universe behaves, so they propose different models. Some of these models appear more likely than others. At the present time, the favored models start with matter in an incredibly dense state that has expanded to the vast system we view today.
Galaxies are giant systems of stars, gas, and dust. In our own Galaxy there are perhaps 1011 stars. Astronomers use an upper-case G to distinguish our Galaxy from other galaxies. Until fairly recently, one might have said that the basic bricks from which the universe was constructed were clusters of galaxies but modern work, probing the depths of the universe, has revealed gigantic structures comparable in size to the largest volumes surveyed.
The largest distances that we may realistically consider are relatively easy to remember, because they are about the distance that light can travel in a time equal to the age of the universe. Our guesses about how old the universe is, and therefore how large it is are uncertain. Until quite recently it would have seemed safe to say the universe was between 10 and 20 billion years old. There is some recent evidence that it is somewhat younger than 10 billion years, but we shall keep the round numbers.
The corresponding radius of the universe is then between 10 and 20 billion light years. A light year is a popular unit of astronomical distances, equal to the distance light travels in a year. Astronomers use another distance unit called the parsec. We mentioned it briefly above. It is a bigger unit than the light year, and arises from measurements of distances to stars. We shall discuss them in a moment. A parsec is 3.1 x 1018 centimeters, or 3.1 billion billion centimeters. There are 3.26 light years in a parsec, so in round numbers, the radius of the universe is some 3 to 6 billion parsecs. Intergalactic distances are measured in units of millions of parsecs, or megaparsecs. Thus the universe is some 3,000 to 6,000 megaparsecs in radius.
It is still debatable whether, if we look on a large enough scale, if the universe smooths out. One of the pillars of the modern theory of the universe is that this must be the case. The universe must look the same in every direction, for every observer. Experts in the field call this the cosmological principle, and all modern theories of the universe assume it.
There is, of course, no proof of the cosmological principle any more than there is a proof of any scientific ``law.'' Like all science, the notion rests on observations (or experiments) for its confirmation. The current situation is that on scales up to about 30 to 100 megaparsecs, galaxies and clusters of galaxies seem to form a network of walls, columns, and voids. The structure has sometimes been compared to that of a sponge.
We need not concern ourselves with these larger structures, because little is known of their chemistry beyond the composition the galaxies and clusters of galaxies that form them. Some very new information is becoming available through the use of distant quasars, but we shall only mention it briefly, when the time comes. The largest aggregate that we shall deal with is the cluster of galaxies. For historical reasons these are not called galactic clusters. The term was already used for certain clusters of stars in our own Galaxy.
The nearest large cluster of galaxies is about 20 megaparsecs away in the direction of the constellation of Virgo. It contains several thousand galaxies, and is perhaps 3 megaparsecs in radius. Another well known cluster is in the direction of Comae Bernices, and is about 5 times further. One of the strangest properties of these giant clusters is that the galaxies are embeded in an envelope of very hot, diffuse gas. The temperature of this gas is so high that it is best observed by satellites that can sample photons at X-ray wavelengths.
The hot gas in clusters of galaxies was unknown prior to space astronomy. The first research dates from the early 1970's. What is so strange about this material is that its mass is significantly greater than that of the galaxies in the clusters! Even though the density of this gas is very low, it is found over such immense volumes that its total mass is impressive. If we average over the entire universe of galaxies as we know it, a substantial fraction of the material, perhaps as much as half(!!), may be in the form of this hot gas. This recently discovered material surely deserves to be called a major constituent of the universe.
Unlike the mysterious, and even more massive dark matter, the hot gas is composed of atomic ions and electrons whose nature we understand relatively well. What is the composition of this gas, and where did it come from? These are significant questions that we must answer.
At about mid-century, several British astronomers considered what they called the perfect cosmological principle. Perhaps the best known of these theoretical astronomers was Fred Hoyle (1915 -- ). Their idea incorporated the ordinary cosmological principle discussed above, but added the postulate that the universe must look the same not only to all observers, but also for all time. It was an audacious concept, but not much more than the cosmological principle itself. An inspiration for the idea may have come from Einstein's Theory of Relativity, in which space and time are treated on an equal footing.
If the universe appeared the same at all times, individual stars and galaxies could evolve, but within a large enough volume of space, history would simply repeat itself, with similar processes occurring here and there, over and over again. There would be little point in trying to reach the most distant galaxies, since whatever was happening in them would also be happening closer by.
If the universe looks the same to all observers at all times, it must be in a steady state, so the theory based on the perfect cosmological principle was said to describe the steady-state universe. But if the universe is expanding, how could it be in a steady state? The originators of this theory answered this question with boldness and panache. They abandoned the notion of conservation of energy at the scale of the universe itself, and postulated that matter could be continuously created out of nothing. This notion may also sound very wierd, but it has a basis in well-established principles of modern physics. There is experimental proof, for example, that electrons and positrons can materialize out of nothingness (or the vacuum) so long as they do so for a very short time.
The steady-state theory surely had aesthetic appeal, yet in the final analysis, it was not accepted. When a universal, microwave, black-body radiation was discovered in the 1960's, almost all astronomers accepted the big bang theory, which predicted it. This cosmic microwave background radiation or CMB is one of the most exciting topics in modern cosmology. The notion of a beginning that is localized in time is at the center of the theory of the big bang, so it is totally incompatible with the idea of a steady-state universe.
It is common to hear the opinion that a given scientific theory has such aesthetic appeal, such beauty, that it must be true. The steady-state theory of the universe is a counter example.
Galaxies come in so many varieties that it is impossible to say that ours is typical. Giant galaxies may be several hundred times smaller in diameter than the Virgo or Coma clusters. Their diameters are several tens of kiloparsecs rather than megaparsecs. The largest may contain some 1012 times the mass of the sun in stars and interstellar matter in the form of dust and gas. There are also dwarf galaxies some 10 to 100 times smaller than the giants.
Possibly the most useful description of the different forms of galaxies is that of the American astronomer Edwin Hubble (1889--1953). His ``tuning fork'' scheme is by no means inclusive, but gives us a good start.
There are two main kinds of galaxies, ellipticals and spirals. The spirals divide into two families, as shown in figure 7-1
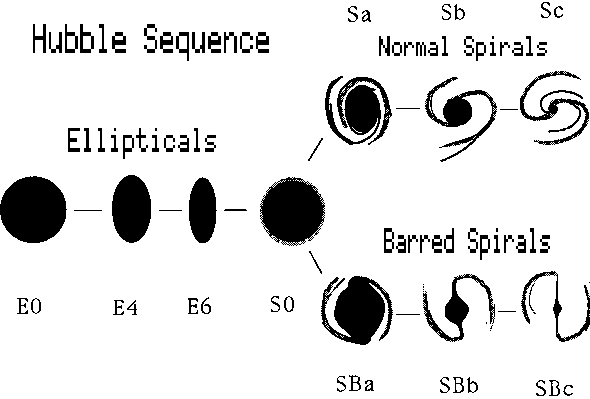
The spirals form two families, one called regular and the other barred spirals. The transition type called S0 may be a spiral that has lost its gas.
The links below lead to illustrations of a few representative types. The designations, refer to numbers in catalogues. The M stands for the early catalogue of the French astronomer Messier in the late eighteenth century. This catalogue differed from previous astronomical catalogues. Since the time of Hipparchus, astronomical catalogues had featured stars or planets. Messier's catalogue featured clusters of stars, and diffuse, bright regions called nebulae. We now know that some of the nebulae are external galaxies, while others are gaseous clouds in our own Milky Way.
M84 is an elliptical galaxy, showing very little structure. M100 is a spiral, while NGC1300 is a member of a family called barred spirals. M104 is a famous spiral seen "edge on" so that the dust lane running through the central plane is prominently seen.
Nearly a century later, a ``New General Catalogue'' (NGC) of stars and nebulae was compiled by the Danish-born astronomer J. L. E. Dreyer.
Elliptical galaxies are rounded or flattened stellar systems. They contain relatively little gas, probably less than a per cent of the total stellar mass. Spiral systems may be rich in gas, especially in the arms, where the star-to-gas mass may be of comparable orders of magnitude. Star formation is clearly going on in spiral arms. If it is occurring in the centers, or bulges of spirals, or in elliptical systems, it is at a relatively low rate.
We can now turn to an overview of the abundances of the elements in galaxies. In our discussion of the solar system, we used four broad categories, metal, rock, ices, and the sun's composition or SAD. These will not be suitable for the present purposes. What basically happens as large stellar systems evolve is that hydrogen and helium are converted into heavier elements. Astronomers have traditionally designated the abundances of hydrogen, helium, and all other elements by the letters X, Y, and Z.
In one of the more bizarre quirks of language usage, Z became known among workers in the structure of stars as the abundance of ``metals.'' Since in most stars, the bulk of the contribution to Z comes from carbon, oxygen, and nitrogen, this is a rather severe misnomer. It arises from a time when it was thought that the bulk of Z was not due to these lighter elements but from iron and its nearby congeners. We shall say more about this when we discuss the history of abundance determinations in stars. For the present, it is useful to use the symbol Z to describe the chemical evolution of stellar systems.
Initially, we may suppose that Z is nearly zero---all of the matter is either hydrogen or helium. As stars evolve and die, in most cases they manage to return some of their mass to the interstellar medium. Because of the processes called nucleosynthesis---the manufacture of nuclei---the returned material has a larger Z than that which formed the star in the first place. Stars may manufacture nuclei rapidly in gigantic explosions, or by slow cooking, but the net result is this slow increase in the average Z for the stellar system. Even in the most mature systems, Z is not very large. In the case of the SAD, Z is about 0.02, so only 2 per cent of the original hydrogen and helium (mass) has been converted into heavy elements (or ``metals'').
In the terrestrial planets, Z is much larger than in stars---more than 0.99. Consequently we needed to talk about entirely different mixtures. Only with the Jovian planets do we reach values of Z that are significantly below 0.99.
The Z-values of spiral and elliptical galaxies follow two quite different patterns. In the spirals, Z is largest where the gas content is least. This effect may be seen both from one galaxy to another, and within a spiral. Z is low in the gas-rich arms and higher in the bulges, where there is relatively little gas. In elliptical systems it is the mass that seems to govern the value of Z. Massive systems have high Z, while dwarf ellipticals have typically lower values.
It is still useful to think of the sun as a typical star. It has a typical mass. Indeed, most stellar masses are contained within 1/10 and 10 times the solar mass. Some stars can have intrinsic brightnesses that are many orders of magnitude greater than that of the sun, but these objects are relatively rare.
We can tell the distances to the stars by a variety of methods. A basic method uses triangulation---observing a nearby star against the background of distant stars. If you hold your finger up at arms length, and alternately open and close your left and right eye, you will see the finger appear to move with respect to objects behind it. This method is used for stellar distances, but instead of a baseline from one eye to another, stars are observed from different points of the earth's orbit. This is illustrated in figure 4-2.
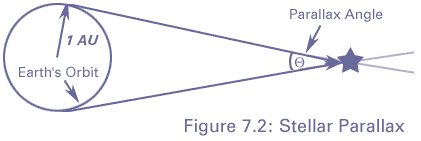
A relatively nearby star appears to move
with respect to background stars when it is viewed from different
parts of the earth's orbit. The angle
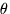 subtended by the
radius of the earth's orbit, as seen from the star,
is defined to be the parallax
of the star. When
subtended by the
radius of the earth's orbit, as seen from the star,
is defined to be the parallax
of the star. When 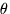 is measured in seconds of arc, then
the distance to the star is said to be d = 1/
is measured in seconds of arc, then
the distance to the star is said to be d = 1/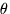 in parsecs.}
in parsecs.}
Most stars are slowly converting hydrogen into helium, and during this process, there is a close dependence of the star's surface temperature and its energy output or luminosity. This relationship is most easily represented with what is called a Herzsprung-Russell (HR) diagram, after the astronomers who first noted it. We show an HR diagram in figure 7-3.
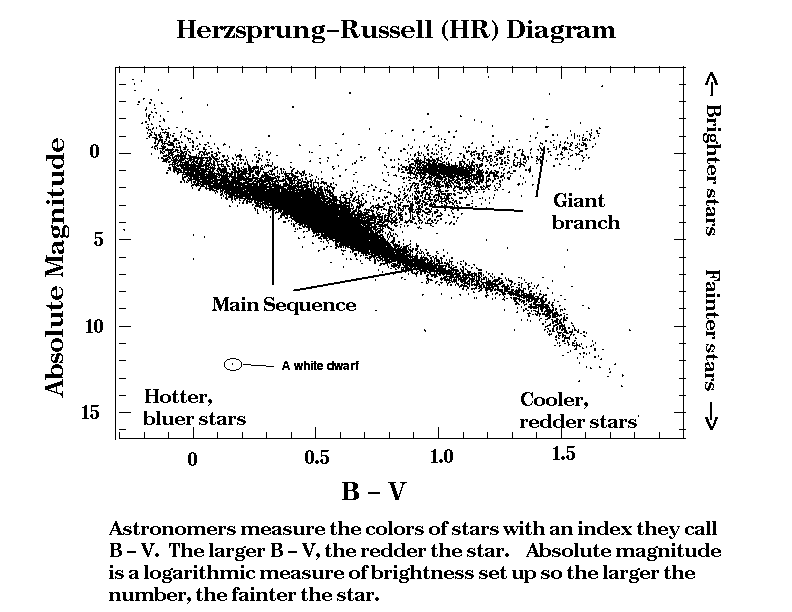
The surface temperature of the stars is plotted along the x-axis, but increasing to the left. The y-axis is the ratio of the intrinsic stellar brightness or luminosity to that of the sun. This plot was made with data collected by the Hipparcos Satellite.
Most stars fall along the main sequence which stretches from the upper left to lower right. Hotter stars fall to the left while cooler ones are on the right. The brighter stars are called giants, and the fainter ones dwarfs. Since the colors of stars indicate their surface temperatures, we may say the main sequence extends from the blue giants to the red dwarfs.
With very few exceptions, we think the surface composition of main sequence stars is the same as the material from which the star was formed. Thus, in the case of the sun, its composition would be the best indication of the composition of the primordial solar nebula. We determine the composition of material at the surfaces of the sun and stars by analytical spectroscopy. This involves the use of an instrument called a spectroscope, which splits the starlight into its constituent colors, or wavelengths. The resulting spectra contain the imprint of the atoms in the material in the stellar atmospheres. We shall have more to say about spectroscopic methods in a subsequent chapter.
In addition to main sequence objects, we also show the location of red giants and (a) white dwarf. The main-sequence stars are said to be "burning" hydrogen into helium. As stars use up their hydrogen, they swell up and become red giants. In later stages of evolution, the stars may explode, or follow complicated tracks that eventually take them back across the main sequence and down to the region of the white dwarfs. These dead or dying stars form a sequence of their own, that is some 104 times fainter than the main-sequence.
We think a relatively small percentage of stars are single. Perhaps 70% are in double or multiple systems. Beyond these multiple systems, triples, quadruples, etc., are star clusters. There are two very different kinds of star clusters in galaxies. In the planes of spirals, there are clusters of relatively young stars that have formed from contracting clouds of gas. These clusters contain from some tens to a thousand or so stars.
In our Galaxy, such clusters are found along the Milky Way, which is really the plane of our system seen from the location of the sun. These clusters of young stars were called galactic clusters because of their location in the galactic plane. Two bright galactic clusters are known as the Hyades and the Pleiades. They are both in the constellation of Taurus, and readily visible in the winter sky.
There is an entirely different kind of cluster associated with both spiral and elliptical galaxies. These fascinating objects are called globular clusters. They are nearly spherical and contain as many as 105 closely-packed stars. A typical globular cluster is shown in figure 7-4. The globular clusters form a spherical halo about our Galaxy, falling within the volumes left unoccupied by the largely flattened system.

M15 is located in the direction of the constellation Pegasus, and is some 15 kiloparsecs away from us. M15 is located well away from the plane of the Galaxy, in the region astronomers call the halo. In this image, the Hubble Space Telescope has enlarged a central portion of the cluster shown in a mosaic to the left. Because of the better seeing above the earth's atmosphere, individual stars can be seen even in the center of this dense cluster.
The globular clusters are old systems, relative to the hotter stars that can be found in spiral arms, and their Z-values are typically lower. The German-American astronomer Walter Baade (1893--1960) discovered that important properties of stars with low Z were significantly different from those with solar and higher Z's. He called the latter stars Population I and the former Population II. Some Population II stars are found in the plane of the Galaxy. These ``general field'' objects are not in globular clusters, although perhaps they once were.
Go out on some moonless summer night and look up at the Milky Way. You can find it by locating the ``Northern Cross'' in the constellation of Cygnus. You may have to drive out in the country to get away from the city lights! The axis of the cross lies nearly along the Milky Way. One side of the summer triangle, the bright stars Deneb, Altair, and Vega, also falls in the Milky Way. The Deneb-Altair side is in the Milky Way, with Vega just to the east.
The band of the Milky Way forms a great circle. It continues south, and returns to the northern sky among winter constellations, where it is less spectacular than in the summer sky. This beautiful band of light is seen when we look along the plane of the Galaxy, as we have already noted. The remarkable Galileo pointed out that this band of diffuse light was due to myriad unresolved stars.
It was only in the present century that astronomers realized the significant role of interstellar dust in dimming starlight in the plane of the Galaxy. Naively, one might expect the Milky Way to be significantly brighter in the direction to the Galactic Center. But as late as the early decades of the 1900's astronomers thought the sun was near the center of a flattened system of stars, because they could detect no concentration of brightness that would indicate a center in any specific direction. We now know that the dimming of starlight is so effective that we just can't see far enough to tell which direction is toward the Galactic center.
Modern astronomical techniques involve observations at wavelengths that were not possible until the latter half of the 20th century. Some of these wavelengths are quite unaffected by dust, so we can ``see'' right through the Galactic center to material on the opposite side. Astronomers began to map out clouds of neutral hydrogen gas in the years immediately following World War II. They used the new radio telescopes, which made use of the radar techniques perfected during the war. Some decades later, still newer methods made it possible to observe spectroscopic features that indicated the presence of interstellar molecules. With these observations, the intimate relationship between dust, gas, and the formation of new stars became apparent.
In the arms of the Galaxy, there are roughly equal masses of stars and gas. The overall fraction of mass that is dust cannot be very large. We know this because dust must be metal, rock, or ice, and these materials have a high value of Z. While the SAD isn't really universal, we can at least use it to estimate what the interstellar Z might be. We have already noted that Z is 0.02 in the SAD. Estimates of the fraction of the total dust to gas ratio are about 1% or somewhat less.
Most of the gas in the plane of the Galaxy is in molecular clouds. There are several thousand giant molecular clouds, or GMC's, and their masses are comparable to those of the globular clusters, up to some 105 solar masses.
It is in these objects that star formation is taking place. In agreement with our notion of the SAD, most of this gas is molecular hydrogen, H2, but in the denser regions of these clouds very complicated molecules occur. These molecules are shielded from the general stellar ultraviolet radiation field by dust. The molecules would be dissociated by the ultraviolet photons without this protection, so the dust is necessary for these clouds to form. Interestingly, the interstellar dust is thought to originate in evolved stars. Thus, there is an interesting chicken-and- egg question regarding these giant clouds and the associated dust.
One theory is that the dust is formed by stars in the general field---not in clusters. The dust then clumps, for reasons that are not understood, and within these clumps molecular clouds can form. Once the molecules form, the clouds can grow, and eventually reach densities where new stars can be formed.
Gas in the GMC's is generally cold gas, but there are also regions in the plane of the Galaxy where the gas is mostly ionized. Astronomers now call these hot clouds H II (H-two) regions. Neutral hydrogen gas is often called H I, so one might speak of either H I or H II regions, depending on whether the gas was predominantly neutral or ionized.
H II regions typically surround hot, young stars, whose ultraviolet photons are capable of maintaining the hydrogen gas in an ionized state. There are also H II regions in our Galaxy where the gas is ionized as a result of shock waves generated by exploding stars. These H II regions show spectra of helium and heavier elements, and it is possible to derive abundances from them. For many years there was little evidence that these abundances were significantly different from the SAD. Recent work however has revealed significant departures from this standard.
It is possible to observe H II regions in some distant galaxies where it would be impossible to determine abundances from individual stars. Much of our knowledge of abundances in distant systems has been derived from these emission regions rather than from stars.
We explored a hierarchy of cosmic systems, starting with the largest structures containing clusters of galaxies. Much of the visible matter in our universe is not in stars at all, but a very hot, diffuse, gas found in clusters of galaxies. We found it convenient to add another category of composition to the crude divisions of metal, rock, and ice, namely, that of the SAD. The SAD contains elements capable of forming the first three materials, but it is 98% hydrogen and helium by mass. By definition, the sun should have the SAD composition.
Galaxies contain globular and galactic clusters. The former are old systems; the latter are young, and in some cases are still forming stars. Young stars are formed in giant molecular clouds, where interstellar dust shields the molecules from ultraviolet radiation from the hottest stars. We may crudely describe the composition of stars and gas using the parameter Z, which is 0.02 in the SAD. As galaxies evolve, we think their compositions change from values of Z nearly zero to those that may be as much as 0.2. In elliptical galaxies, Z is correlated with the mass of the systems, while in spirals, it is most closely related to the gas fraction. Spiral systems that have used up their gas have high Z.
Astronomy is the study of objects within the universe beyond our earth. Traditional astronomers learned about these objects by studying their light. Initially, it was enough to be able to measure accurately the relative positions of light from the planets and the stars. Eventually, astronomers were able to analyze this light itself, with the help of instruments known as photometers and spectrographs. For many centuries, astronomers could only study light from objects that fell on their eyes and telescopes here on the earth. In the second half of the twentieth century this changed completely as a result of the space program.
Courses in astronomy are typically divided into two parts. Traditionally, the solar system has come first, followed by everything else--stars, galaxies and the universe. Observations from space vehicles have had a profound influence on all aspects of astronomical research. But the case of the solar system, changes due to the space program have affected astronomy in a fundamental way that does not have a counterpart in the study of stars and galaxies. Space vehicles have carried instruments, and in the case of the Moon, astronauts directly to the astronomical bodies under study.
This is an advantage does not exist for stellar or galactic astronomers. The space program gave them access to new windows into the astronomical universe, but it remains necessary for them to study their objects from afar.
Let us contrast briefly, the approach to the study of nearby objects and those so distant that we can only analyze their light. This was the situation for the solar system in the years prior to the space program. What kinds investigations were carried out in these days, and how can we contrast them with current studies?
Isaac Newton's laws of gravitation and mechanics provided the basis for an understanding of the motion of planets about the sun. For nearly two centuries, astronomy was dominated by the problem of refining our understanding of the motions of the planets and their satellites. A triumph of these endeavors was the discovery of the new planet Neptune. In most of this work it was not necessary to think of the planet as a body at all. In the equations that described planetary motion, it was usually sufficient to describe the motion of a "point mass," something with the mass, but not the physical size of a real body.
Thus, during much of the nineteenth century, planets were not thought of as worlds in their own right at all, at least by many scientists. It may be that the early science fiction writer, Jules Verne, had a broader view than some astronomers of his day.
Toward the end of the nineteenth century, telescopes became powerful enough to reveal hazy features on Mars, and there was a definite time in which that planet was thought of, at least by a few, as a real world of its own. The problem was that we could only look from a great distance, and we shall learn the ideas formed at this time were so far off the mark that they discouraged this general approach as belonging to crackpots.
With larger telescopes, photometers and spectrographs, it became possible to do rudimentary planetary astrophysics. We could get a rough idea of the temperatures at the surface of Mars, and the outer layers of the Jovian planets. With the help of the spectrograph, we were able to identify chemicals in the atmospheres several planets.
Prior to the space program, our picture of the planets resembled a time table and a list of measurements. Not very exciting stuff.
With the return of the first rocks from Apollo 11, our view of the Moon and planets changed forever. Although close up pictures had been taken of the Moon's surface, and landers had actually returned information from it, we weren't sure what sort of material made up the Moon's surface. The returned samples told it all. The moon's surface was made of rocks and minerals, similar in many respects to materials well known to terrestrial geologists.
In a very short time, the Moon became a world in its own right, to be studied by entirely new tools. The discipline of planetary geology burgeoned. The Moon had extensive lava flows not unlike those known in the northwestern part of the US, or the Deccan plateau of India. The moon had faults and graben, scarps and lava tubes, all of which were known on the earth. But the Moon, and as we later learned, many other planetary surfaces were heavily scarred by impacts.
Eventually, our thinking about the processes that created the scars on the Moon, Mercury and Mars began to influence our view of the earth's history--and very recently, its future as well. We now think the terrestrial planets and many satellites were assembled from interplanetary debris, the last of which fell violently onto the nearly completed surfaces. Eventually, the rate of infall declined, but never became zero. Today, we are rightly concerned about the effects on the Earth of an impact of a large meteoroid or comet.
Today our knowledge of the planets comes primarily from close up images taken by space probes. Take this link for a listing of past and planned NASA missions to planets. Much new information about the solar system also comes from the laboratory study of moon rocks and meteorites. The tools of the modern planetary astronomer are very different from those who analyze the light from distant stars and galaxies. One fundamental difference is that the light from stars and galaxies comes mostly from material that is gaseous, and under relatively low pressures. Moreover, they are typically hot enough that chemical reactions are of minor importance.
The significant processes that influenced the history of the planets have been largely chemical. This is because the relevant temperatures have generally not been high enough to prevent chemical bonding. Chemistry is irrelevant for most (not all) of the sun itself, because of its high temperature, but for the planets and their satellites, chemistry is unavoidable. Most of the chemicals that form the terrestrial planets are in the form of minerals, and the minerals form rocks. The study of rocks and minerals are a specialized domain of chemistry, emphasized for obvious reasons by geologists.
Our introduction to the new astronomy of the planetary system must therefore review some of the fundamental concepts from chemistry and geology. Now that we can visit these bodies, we must study them with the appropriate tools. They are worlds in their own right, and we must apply methods to them learned in the study of our world. These methods are surely more elaborate than those necessary to the classical approach when we could only "look at" the planets. Fortunately, we do not need to become full fledged chemists or geologists to understand the new solar system. Many of the necessary concepts have been presented in high school courses in chemistry and general science. We will devote a few lectures to these topics at the appropriate time. But the new approach to the solar system has this additional complication--we have to know some general science.
One persistent theme of this course is that the history of matter is written in its abundance patterns. This means that if we can determine the chemical composition of objects in the universe, we can learn much from this about how these objects were made, and how they evolved--their history.
Astronomers have traditionally been asked about the possibility of life on other worlds. Aside from the small matter that they typically know rather little life science, they are the ones who study these worlds, so in spite of their ignorance, they rarely are without some words on this matter. If planets are worlds, and the earth is a planet, then since life arose on at least one planet, the question of the origin of life should also be a part of the new science of the solar system.
Our understanding of fundamental biological processes has burgeoned in the years following the discovery of the double helix. We now understand the basic processes by which current life forms exist and reproduce. But we are very much in the dark about how it all got started. In this course we will learn enough about the biochemistry of the cell to understand how far today's living cells are from the simple organic molecules found in meteorites and interstellar space. In spite of this huge gap in complexity, most scientists believe living material arose from nonliving matter through the action of chemical processes. These processes are thought to be understood in principle, if not in detail.
Our understanding of the world we live in accelerated as a result of the adoption of the scientific method. Briefly, this method is one by which we learn by making observations or performing experiments. An alternate way of learning is by consulting books or authorities. This is OK in science, provided the authors or authorities based their knowledge on observations and experiments.
At about the time of Galileo (1564-1642), western scholarship was just breaking away from the notion that sacred texts were the proper source of knowledge about the world we live in. Galileo performed experiments and made observations, and his interpretations conflicted with those of powerful churchmen of the time. These authorities made life difficult for Galileo, but their reign as curators of ideas and views was coming to an end. Today, Jesuit priests at the Vatican Observatory do active astronomical research, but their science and religion do not seem to overlap.
People often mean different things when they discuss the scientific method. Philosophers of science have probably written more about the method than scientists.
(a) They often include in the notion of the method, psychological factors that affect the way scientists do their work, such as jealousy, anger, fatigue, irritability, ambition, etc. There is no doubt that these factors are relevant to the history of science. On the other hand, most scientists think
(b) the scientific method starts with data and the formulation of hypotheses, and proceeds to tests. The hypotheses may be modified, and further tested. Ultimately it is the consistent agreement of the hypotheses with the tests that is the basis for accepting any theory as valid.
The practice of deciding whether we should believe something by observing is hardly restricted to traditional science. If you want to know which store has the best bargains, and go out and check the prices, that's using the scientific method. Even though you may not feel like a scientist, strictly speaking, you are doing science.
The scientific method is a cyclical process that ends when a theory and relevant observations or experiments are in agreement with one another. The important point is that the decisions about the validity of ideas are based on the experiments and observations and not on the "authority" of some person or book. I like to think of "scientific" conclusions as based on a sliding scale of confidence:
false true
^ (confidence) ^
| <-----------------------------------> ||
----------------------------------------------
^
|
science
In science, we never get all the way to true. There is always the possibility of a new observation that doesn't agree with our theory. Usually what happens is that we learn to live with a limit of validity, that is, we find the theory is OK within some domain, and we just can't use it outside of that. This is the situation with Newtonian mechanics. So long as we don't deal with very small things, or very high velocities, the theory is OK.
Since we can never perform all possible tests, we can never have rigorous truths or facts. Contrast
Discipline Method Conclusions
---------- ------ -----------
mathematics, logic deduction true or false
science induction confirmed or falsified
(in some domain)
Induction means generalizing or abstracting from specific instances, while deduction is more or less the opposite. Here we assume some general principle, and work out the consequences by the rules of logic.
In scientific work, as ideally carried out, it is necessary to keep an open mind, and to make one's own decisions based on observations. As much as possible, conclusions should NOT be based on some authority. But in practice, we must have some faith. How in practice does one decide whom to trust?
Here is one guide. Most scientists will trust someone they think has done the experiments or made the observations, and isn't just quoting someone else or some book. The "Laffer curve" once played a role in economic decisions of the Reagan administration. Laffer is an economist who, the story goes, drew a graph on a napkin one evening at a restaurant to illustrate a point for his companion. This curve was supposed to display the effect of taxation on governmental revenues. His idea was that at some rate, governmental revenues would actually decline as taxes went up. If people were taxed more than some limiting amount they wouldn't make the effort to earn more. Therefore, if one cut taxes, government revenues would actually increase. In the story (which is all we need to worry about here) Laffer's idea came out of his head rather than from data. The curve reflected the way he thought the system would respond rather than conclusions based on considerations of real data. The economic text of Samuelson and Nordhaus shows a curve based on what they considered a more careful study--not just drawing on a napkin. The curve was significantly displaced in such a way that no projected gain of governmental revenues would result from a tax cut unless the peak rate were much higher than 50%.
Another guide to the reliability of scientific conclusions is called "peer review." After we do a piece of research, we may summarize it in a "paper," and send it to a journal. The editor of that journal will send the paper to someone also working in the field for evaluation. Typically, that person will recommend some checks or minor changes. Sometimes the paper is modified as a result of these checks, but often minor stylistic changes are made.
Peer review has some nightmares, where a referee will behave inappropriately. Papers may be rejected by a referee because of personality problems between author and referee. Often, a journal editor will know of such situations, and avoid sending someone's paper to a scientific adversary, but not always. Peer review has many flaws but it is hard to think of a better system.
You may have heard of the author and lecturer Richard Hoagland. He has published a book about Mars that I would call junk. I checked (10 January 1999) the library's MIRLYN data base to see if the author-lecturer Richard Hoagland had published recently in any refereed journals in physics or astronomy. My search of the data base revealed nothing, and this confirmed my suspicion that this fellow is nothing more than a performer, and not a scientist at all.
Let us contrast the four physical sciences. Physics and Chemistry provide the rules or laws, for example, the law of gravitation, the quantum theory, or thermodynamics. As far as we know, these laws are constant in time. IF THIS WERE NOT THE CASE, THE SCIENTIFIC METHOD AS WE KNOW IT WOULD BE IMPOSSIBLE. If these laws changed with time, we could never confirm anybody's results. The essence of the scientific method would be undermined. Therefore:
Astronomy and Geology have a historical dimension not present in physics or chemistry. An iron atom now is the same as an iron atom 1000 years ago. It was the same as an iron atom 109 years ago---we think. Chemicals are the same now as 109 years ago, as far as we know. On a 1000 year time scale the Earth hasn't changed much, but on a 108 year time scale, it has changed a lot. This is the time scale for continental drift. Even if we go back only tens of thousands of years we get to ice ages. If we go back several billion years (several times 109 years) we approach the time of the formation of the earth.
109 years ago, the sun was not too different from what it is today, but 1010 years ago, the sun had not been formed, and 1010 years from now, the sun will have died--it will have become a white dwarf. Prior to this it will become a red giant, and have burned our earth's surface to a crisp.
The notion that biological processes can be reduced to the laws of physics and chemistry is called reductionism. It is the viewpoint taken in these lectures. There is no way to prove that reductionism is the "correct" view, but steady progress has been made by those who have proceeded as though it were true. In the past several decades, the most notable examples of progress in understanding life science in terms of physics and chemistry are in the field of molecular biology and genetics.
Reductionists admit they cannot predict anything so complicated as the herd instinct of buffalo, or even the detailed behavior of life at the cellular level. But they may claim these matters are understood "in principle." What this means is that they believe they have the recipe to understand these matters, but not the computational power to follow it. They would say that the recipe is contained in the laws of physics and chemistry. But just to predict the detailed behavior of matter on the cellular level requires the solution of a problem containing some 1023 atoms. Any physicist will tell you that even a problem involving 3 bodies cannot be solved in a closed form, and must be solved by numerical methods.
Modern computational methods are now capable of tracking simple interactions among hundreds or even thousands of bodies, at least for short periods of time. Methods of treating macroscopic matter, e.g. 1023 atoms, involve approximations and gross averages. But, a reductionist would say, if we had the computing power, we could solve the problem as accurately as needed. This is what they mean when they say a problem is solved in principle.
| 1. How has the space program changed the way astronomical objects are investigated? |
| 2. Think of one or more examples where the history of matter is reflected in the abundances of that matter. |
| 3. What is the difference between "the scientific method" and various methods used by scientists? |
| 4. In what sense can we say that astronomers and geologists are interested in the history of the objects they study, while chemists and physicists are not? How is this idea connected with "the scientific method"? |
| 5. Compare and contrast induction and deduction as methods of reaching conclusions. |
The study of astronomy is traditionally divided into (1) the solar system, and (2) all else: stars, galaxies, and the universe. The space program has made it possible for planetary research to be carried out, in many cases, on site. To take advantage of close-up views and in some cases, actual samples of planetary materials, the modern planetary astronomer draws on a wide variety of scientific disciplines. Many aspects of geology and chemistry are now relevant. The planets are no longer objects that can only be studied with the aid of ground-based telescopes. Space probes have revealed them to be worlds in their own right, and tools honed in the study of the Earth are now appropriately used in planetary astronomy.
Science is done by those who pursue the scientific method. We use the term to mean that conclusions are based on experiment and observation: induction, rather than authority or pure deduction.
Of the four physical sciences, astronomy and geology have a historical dimension that is lacking in physics and chemistry.
We shall take the reductionist point of view, and suppose that life science can be explained in terms of physics and chemistry. There is no way to prove this.
In this lecture we will review some elementary calculations and mathematical tools that are necessary for an understanding of many aspects of astronomy.
"Astronomical" numbers are easier to manipulate if we use powers of ten. The sun is roughly 93,000,000 miles from the earth. It's easier to write this as 9.3 x 107 miles. If we have two numbers expressed as powers of ten, we can multiply the numbers in front of the powers of ten, and add the exponents. Thus, suppose we want to convert the 9.3 x 107 miles to its equivalent in kilometers. The conversion factor is 1.609 km/mile, but we may write this as 1.609 x 100 km/mile, or as 16.09 x 10-1 km/mile, or 0.1609 x 101 km/mile.
Readers should convince themselves that if we multiply the 9.3 x 107 miles by any of the three forms of the conversion factor, we get 1.496 x 108 km. This is very nearly 1.5 x 108 km, an easy number to remember for the distance from the Earth to the sun.
Powers of ten are also useful for small numbers. The wavelength of the yellow light of a candle flame is about 0.000059 cm (centimeters). We can write this as 5.9 x 10-5 cm. Astronomers use the Angstrom unit when discussing light. One Angstrom unit is 10-8 cm. Therefore, yellow light has a wavelength of some 5,900 Angstrom units.
Any number can be expressed as a logarithm. In these lectures, we'll only worry about the logarithm of positive real numbers, and we'll only use logarithms based on 10. Thus, if x and y are numbers, and y is the log of x, then by definition, x = 10y. The logarithm of any power of 10 is therefore just that power. For example, if x = 106, the log of x is 6.
Exponents get added when you multiply numbers:
22 x 24 = 26.
The same thing holds for powers of ten. So if you add the logarithm of two numbers, you get the logarithm of the product. Suppose z = 10y, and r = 10s. Then
zr = 10y+s
or log(zr) = y+s. Calculators make it easy to take logarithms, because all you have to do is push a button. But you should check to see that you get the same thing if you take the log of 1.5 x 108, or if you take the logs of 1.5 and 108 separately, and add them together.
Logarithms will be used in an exercise in the sections to make astronomical distances easier to think about.
We will often encounter the proportionality by equating two fractions: a/b = c/d. Typically, we will know three of these four numbers, a, b, c, and d, and we will need to find the fourth. It's best to manipulate the relation so the thing you need to know, the unknown, is on the left of the equal sign, and the things you know are on the right. For example, if d were the unknown, we'd first write the equation as
cb
d = -------,
a
and then punch the numbers in the calculator.
In this course, we won't get relations much more complicated than this, but sometimes we'll have to move quantities from one side of an equation to another in addition to cross multiplication. For example, if
ab ---- + c = f, y
and you need to know y. First move the c to the right, so you have
ab --- = f-c y
and then cross multiply, to get
ab ab ------- = y or y = ------- f - c f - c
It's almost always best to solve first for the thing you want, and then put in the numbers. That's because symbols are usually shorter and easier to move around than the numbers they stand for. So solve first using the formula, and then put in the numbers.
Many distances in astronomy depend on
triangulation. We will make considerable use of skinny triangles.
having a central angle  .
.
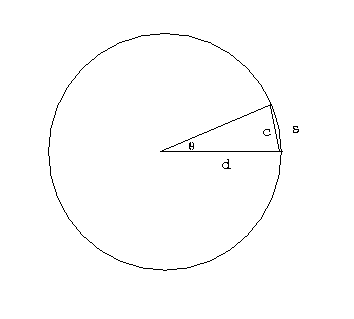
Then if the radius of the circle is d, and the arc
with the angle  is s,
is s,
(deg) s ----------- = ----------- (1) 360 (deg) 2
d
It is important to note that if  is small,
that is, if the triangle is really skinny, then the arc,
s, and the straight-line chord, c, are very nearly equal.
So if you forget, or never learned trigonometry, you may use
simple proportions to analyze distances and angles in a skinny
triangle.
is small,
that is, if the triangle is really skinny, then the arc,
s, and the straight-line chord, c, are very nearly equal.
So if you forget, or never learned trigonometry, you may use
simple proportions to analyze distances and angles in a skinny
triangle.
Suppose we want to put  in seconds of arc. We have
in seconds of arc. We have
6 360 (deg) x 60 (min/deg) x 60 (sec/min) = 1.2960 x 10 (sec) (2)
Note how the units on the left cancel, so that only sec remain for the right. Carry the units along in your own work. It is a big help.
The radian is an angle, defined in such a way that if
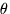 in Equation (1) is 1 radian, then s equals d. If we put s = d in (1),
and solve for
in Equation (1) is 1 radian, then s equals d. If we put s = d in (1),
and solve for 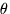 (deg), we get
(deg), we get
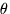 = 360 (deg)/2
= 360 (deg)/2  , or
1 rad = 57.30 (deg).
, or
1 rad = 57.30 (deg).
To find the number of sec in a radian, we divide the number of
seconds in a full circle, given by Equation (2), by
2 . The result is
206264.81, which astronomers usually round to 206265.
Thus the unit of length, which astronomers call the parsec,
is 206265 times the earth-sun distance (the astronomical unit).
We shall discuss the parsec in more detail below.
. The result is
206264.81, which astronomers usually round to 206265.
Thus the unit of length, which astronomers call the parsec,
is 206265 times the earth-sun distance (the astronomical unit).
We shall discuss the parsec in more detail below.
If we measure 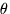 in seconds of arc,
s in astronomical units
(AU), and d in parsecs (pc), we can write (1) in the form
in seconds of arc,
s in astronomical units
(AU), and d in parsecs (pc), we can write (1) in the form
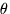 (sec) s (=1 AU)
--------------- = --------------------------- (3)
206265 sec d (pc) x 206265 (AU/pc)
(sec) s (=1 AU)
--------------- = --------------------------- (3)
206265 sec d (pc) x 206265 (AU/pc)
This gives the simple relation
d (pc) = s(AU)/[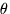 (sec)]. Since in
stellar parallax, s is always 1 AU (we use the earth's orbit), this
relation is even simpler: d = 1/(
(sec)]. Since in
stellar parallax, s is always 1 AU (we use the earth's orbit), this
relation is even simpler: d = 1/(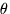 ),
where it must now be
understood that the distance is in parsecs and
),
where it must now be
understood that the distance is in parsecs and
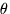 in seconds of arc.
This value of
in seconds of arc.
This value of  is called the parallax.
is called the parallax.
A final ubiquitous relation that we shall need is the following:
Amount = Rate x Time (4)
Note that this is true if (1) the rate is constant over the relevant time, or (2) if we use an appropriate average rate for the relevant time. We will (almost) always be able to assume one of these two alternatives.
The most common use of this may be the form
or distance = velocity times time, but in another form it says
or velocity = acceleration times time.
Another useful example of (4) is to determine the lifetime of some process that is going on at some average rate. For example, we can determine the lifetime of the sun if we know how much energy it has to expend, say E, and the rate that it is expending that energy. Astronomers call that quantity, the sun's luminosity, L. So E = L x t, or t = E/L. Astronomers think they understand the sun well enough to say that its lifetime is about 10 billion years.
In this course, we will mostly use simple algebra, that requires nothing more than moving things from one side of an equation to another and cross multiplication. We generally avoid trigonometry with the help of the skinny triangle, whose analysis only requires that we set up a simple proportion. In our equations, we encountered units (cm, km, AU). It is important to keep these units with the quantities they belong to. As we shall see, this can help us to avoid errors. We also introduced the important relation: Amount = rate x time.
The sun is more massive, by slightly more than a thousand, than the giant planet Jupiter. While we know its mass and volume quite accurately, we cannot use its density to infer its composition because much of the sun is a highly compressed, ionized gas. We infer the bulk solar composition from spectroscopic analyses of the visible atmosphere. It is useful to think of the sun as an average star. Thus, if we say that there are 1011 stars in a galaxy, the mass of that galaxy should be some 1011 times that of the sun, and its luminous output about 1011 times that of the sun. The sun's mass (MSun = 2 x 1033 grams) and luminosity (LSun = 4 x 1033 ergs/sec) are about the same in the cgs system of units. The mean density of the sun is also about 1 gm/cm3.
The part of the sun from which the light comes to us is a gas with a mean temperature of about 5800K. The average, visible surface of the sun is called the photosphere. Above the photosphere is a very inhomogeneous region some 10 to 20,000 km in thickness. It was first noted during solar eclipses, where it is seen as a colorful, red arc called the chromosphere. Beyond the chromosphere, for several solar radii the diffuse solar corona merges with the solar wind. Energy of motion from subphotospheric regions are carried by sound waves which heat the chromosphere and corona. The temperature of the corona is typically a million degrees Kelvin.
The gas in the corona is very thin, so that its high temperature has little effect on the photosphere. Somewhere in the low chromosphere, a temperature minimum occurs. The temperature rises both inward, toward the solar interior, and outward into the chromosphere and corona.
A typical gas pressure in the photosphere is about a tenth that at the earth's surface. There are a few molecular fragments, but most molecules are dissociated. These are mean conditions. At any point on the surface of the sun, conditions can vary wildly. Hot gas from below flows upward, while cooler gas descends. This method of transporting heat is called convection. Conditions in the hot and cold streams can show large fluctuations, and it is amazing the solar surface seems so uniform and constant.
One of Galileo's many discoveries was sunspots. It is not difficult to see sunspots with some optical aid. Of course, one should never look directly at the sun with binoculars or a telescope, but it is easy to project the solar image on a white card, and then sunspots are readily found. These are regions a thousand or more degrees cooler than the 5800K mentioned above. They are incredibly complex regions, with strong concentrations of magnetic fields, and complicated gas flows.
If one observes sunspots day after day, one finds that they appear on the east limb (or edge) of the sun, pass across its face, and disappear at the west limb. This coming and going of sunspots had been observed by Galileo and others toward the end of the 1500's. Galileo correctly concluded that the sun was rotating, with a period of about 27 days. It is hard to imagine, but nevertheless true that this conclusion posed a difficulty for some of the observers. In particular, Christoph Scheiner, a talented Jesuit scientist, had been warned by his superior not to discuss spots on the sun, because they had not been mentioned by Aristotle (384-322BC). Scheiner published his findings anonymously, concluding that the spots were small, dark bodies circling the sun. In this way, he avoided the problem that spots on the sun had not been mentioned by Aristotle--but as the author Isaac Asimov wrote, Aristotle hadn't mentioned the small, dark orbiting bodies either!
Probably no one would have predicted sunspots if they hadn't been observed. It is perhaps a lesson for anyone who does science to realize that nature can be very complex. Regions of the sun that we cannot observe directly are thought to be considerably simpler than the surface.
Sunspots had been known for more than 200 years before it was discovered that they went through a cycle, becoming more plentiful roughly every 11 years. It wasn't until the early 20th century that it was realized sunspots contained strong magnetic fields. Sunspots often occur in close pairs, a leader and a follower, in the sense of the sun's rotation. The magnetic polarity of the leaders and followers are typically opposite. If the direction of the field of a leader is north, that of the associated follower will be south. It was also found that the polarity of spot pairs in the northern and southern hemispheres were opposite to one another. If the leaders in the northern hemisphere have northern polarity, the leaders in the southern hemisphere have southern polarity.
Early in this century, it was discovered that the magnetic cycle of the sunspots was double that determined by simply counting the number of spots on the sun. Leading and following spots change their polarity in alternate cycles. So if the leaders (in either hemisphere) have northern polarity in one cycle, they will have southern polarity in the next cycle.
A wide array of activity is associated with sunspots. Giant plumes of gas called prominences may hover in the neighborhood of spots. They are typically near large spots, which tend to be complex, rather than having the simple form of a bipolar group. The darkest, central regions of spots are called their umbra. These are surrounded by a less dark region, the penumbra, which are still darker than the general photosphere. Still further from the spots, the solar surface is just a little brighter than the general photosphere.
It usually takes special instrumentation to see the bright regions surrounding sunspots, which are called faculae, but the brightest may be seen on a projected solar image, in "white light." Occasionally, large amounts of magnetic energy are released in the neighborhood of a sunspot, giving rise to a solar flare. These flares send shock waves through the outer solar atmosphere, and accelerate particles which may reach the Earth and cause electrical storms and aurorae.
Many additional facts about the sun, and a very useful glossary are available from the National Solar Observatory/Sacramento Peak.
What the astronomer does to understand the interior of the sun, and indeed of any star, is to make a mathematical model. The procedure is similar in nature to models of planetary interiors. These models are constructed by requiring that the pressures at any depth must be enough to hold up the mass of the overlying layers. The relevant principle is known as hydrostatic equilibrium.
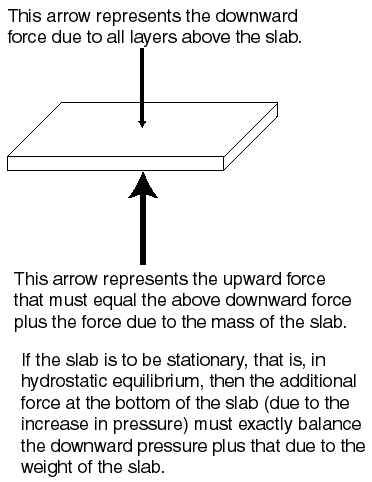
(You may want to read ahead in Lectures 10 and 11, where pressure is defined.) We start at the ``top'' where the pressure is very low, and consider a layer of material with the conditions we think exist there---the temperature and pressure. This (conceptual) layer has a certain mass, so we ask what the pressure must be at the bottom to support it. As we proceed from one layer to the one under that, the pressure must steadily increase. Along with the pressure increase, there is usually an increase in temperature although this is not essential for hydrostatic equilibrium.
Some atoms may lose electrons as a result of the increased temperature, for example. So we have slightly new conditions for the material that makes up the next layer. We take these into account in calculating its mass, and we add this mass to that of the layers above it in order to get the pressure at the bottom of the new layer. These procedures are followed until we get to the center, where the pressure must be sufficient to hold up the entire star---or planet.
The structure of the solar interior is thought to be rather well understood, although a few mysteries remain. If the sun were originally uniform in composition, then theoretical models predict the rate at which hydrogen is being converted into helium in the regions near the center. This conversion, of course, takes place by nuclear reactions, whose rates are believed to be rather well understood. However, it may be that we don't quite know all that we need to know.
For some thirty years now, there has been a discrepancy between the observed and predicted numbers of elementary particles known as neutrinos which should be produced in the solar interior. This discrepancy is one of the major unsolved problems of stellar astrophysics.
The neutrinos are produced by the nuclear reactions that supply the sun's energy. They interact only very weakly with matter, so they emerge from the solar interior and stream out into space. A certain number of them must pass through the earth, and with very careful measurements, physicists have been able to detect them.
Much recent discussion has centered around the possibility that the problem may not lie in the astronomical domain at all, but in that of particle physics. Roughly half the neutrinos that should have been detected actually were. It is possible that some of the neutrinos changed their form in flight from the sun, and this might account for the low measurements.
Neutrinos come in three flavors, and if they ``oscillate'' from one form to another, the consequences could be of considerable importance for the dark matter problem that we have mentioned earlier. The neutrino oscillations might occur because these particles have what is known as a rest mass.
According to special relativity, the mass of a particle will increase as its velocity approaches that of the speed of light. If a particle has any mass, no matter how small, when it is at rest, it cannot be accelerated to the speed of light. Therefore, photons, which by definition travel at the speed of light, can have no mass when they are at rest, and therefore, there is no such thing as a photon at rest.
It is not known if neutrinos are like photons, with no rest mass at all, or if they have very small masses, and travel at nearly (but not exactly) at the speed of light. If the latter situation turns out to be true, we may not only solve one of the outstanding problems of the structure of the sun. We may also solve one of the main problems of the structure of the universe itself, for it might be that the missing or dark matter could be explained by massive neutrinos.
The sun contains all but about 0.1% of the mass in the solar system. Therefore, we take the standard abundance distribution (SAD) to be that of the sun. Hydrogen is slowly being converted into helium, in the sun's core, thus supplying the output that has kept the sun at roughly the same luminosity for nearly 5 billion years. Energy passes from the core of the sun into an envelope that then transports it to the surface mostly by convection. This convection is responsible for much of the solar activity, such as sunspots, prominences, and flares.
The late physician and author Lewis Thomas described medicine as The Youngest Science. Before the days of penicillin, Thomas wrote, much of medicine involved letting the body cure itself, and taking a little credit for it. Penicillin was discovered in 1939. Clearly in our time, medicine as a science is rapidly maturing, and we will explore some of the basis for this in our last lectures.
How is it that astronomy is the oldest science? This may go back to prehistoric times, when hunting and gathering tribes migrated with the seasons and ice ages. There is no evidence that people today any more intelligent or canny than those of the earliest civilizations. The emergence of modern man, Homo sapiens sapiens, is thought to have taken place some 100,000 years ago. That's 100 millenia (!!), an interval of time an order of magnitude longer than historic times. It's unthinkable that clever people didn't realize the advantage of finding their way with the help of the sun and the stars.
Prior to the development of the ship's chronometer, navigators would sail along a parallel of latitude, keeping the north star at a constant elevation above their night horizon. The same trick would work on land, and was probably used by the hunting and gathering tribes. These people lived under skies that were unpolluted by smog or city lights. For them, the stars and planets shone with a brilliance few can enjoy today. Surely these people knew and used the astronomical phenomena as guides.
There is recorded evidence, several thousand years before the birth of Christ, of astronomers as timekeepers in the river valleys of the ancient civilizations along the Nile, Tigris and Euphrates, and Indus valleys. These rivers overflowed seasonally, and it was important that somebody keep track of the time of year so the farmers could prepare for the floods. Primitive calendars were based on the Moon as well as the sun, and these ancient bookkeepers struggled with the unfortunate fact that the number of lunar months in a year is not an integer.
Whether we call these ancient timekeepers astronomers, or priests, is not important. What is significant is that they knew enough not only to predict seasonal floods, but eclipses too.
Similar eclipses occur at intervals of 18 years plus 11 days called the Saros. The period was known to the Babylonians, some two thousand years before the birth of Christ. It is true that all one needs to recognize the Saros are records, but we are speaking of a time when written records were kept by a select few. These early astronomers had to test the hypothesis that the Saros was significant by predicting a "next" eclipse. They therefore must have qualified as scientists, even though their understanding of celestial phenomena could not have been very profound.
The techniques of these scientists-priests, to keep track of time and to do the necessary arithmetic to make their predictions, was both sophisticated and mysterious. Those who could do it gained in stature. Success in the prediction of natural phenomena, such as the seasons and flooding, surely led some scientist-priests to try their hands at prediction of the future for people as well. In this way, the quack science of astrology was born.
I once saw an interview on TV with an individual who claimed to be an astrologer. He complained that astronomers always trashed what he did, even though they knew very little about it. He said he once challenged three astronomers during a debate to describe how a horoscope was cast, and that only one of them could even make a start. That one couldn't do it correctly. Well...I couldn't cast a horoscope either. So you must record it as merely my opinion that astrology is at best entertainment, and at worst foolishness. Life is short, and I have made the choice to pursue other matters than astrology--just so I could debate an astrologer on his turf.
The earliest astronomer whose name we should remember is Aristarchus (320-250BC) of Samos, an island off the Turkish coast peopled by Greeks. He is sometimes called the "Copernicus of antiquity" because of his heliocentric view of the solar system. He even tried to determine the relative distance of the sun and Moon by timing the interval between quarter phases of the Moon. The sun is nearly 400 times the distance of the Moon, so to make an accurate determination using Archimedes method, it would be necessary to distinguish between the times from third quarter to first, and from first to third to considerably better than one part in 400, which was beyond the technology of that time.
A second ancient astronomer is Eratosthenes (276-196 BC), who is best known for a determination of the circumference of the earth. In order to do this, he had to have known that the Earth was round, a fact that was doubted until well into the middle ages. When I began to study astronomy in the early 1950's, all the textbooks offered "proofs" that the Earth is round, or strictly, spherical. These books would point out, for example, that when ships disappear over the horizon, the hull disappears first, and the masts last. This is most easily explained if they are moving over a curved surface. It is sometimes amusing for me to think that modern astronomy texts omit such proofs, and that they were hardly necessary at any time in the 20th century.
Eratosthenes noted that the relative position of the noon sun, on the day of the summer solstice, was different when viewed from Alexandria (Egypt) and Syene (the modern Aswan). At Syene, the sun was directly overhead--at the zenith--then. According to the story he noticed that it shown directly down a deep well. But at Alexandria, to the north, the sun was less than 900 above the horizon--not quite to the zenith.
To find the circumference of the earth, Eratosthenes set up essentially
the same proportion we used to discuss the
skinny triangle. In this case
 is the angular distance between Alexandria
and Syene, as viewed from the center of the earth. The arc, s,
is the distance between the two sites. We don't need to use the
chord, c, at all, since the unknown is the earth's circumference.
The proportion is:
is the angular distance between Alexandria
and Syene, as viewed from the center of the earth. The arc, s,
is the distance between the two sites. We don't need to use the
chord, c, at all, since the unknown is the earth's circumference.
The proportion is:
circumference/360 = s/
Hipparchus (190-120 BC) may have been the greatest, if not the most influential of the Greek astronomers. Like Eratosthenes, he was a member of the Alexandrian Greek culture. His accomplishments were many, but we shall only note three here. He made an accurate map of the sky, and introduced the system of brightnesses still used by astronomers today. He also discovered the phenomena called precession of the equinoxes, discussed below.
The brightest stars were called "first magnitude," with those just visible to the naked eye, "sixth magnitude." It was discovered by the astronomer Pogson in the late 19th century, that the interval of 5 magnitudes (1 to 6) corresponded closely to a factor of 100 in the energy output of stars measured at the earth. Pogson is known for little else, but the brightness ratio of stars with one magnitude separation is now called "Pogson's ratio." It is the fifth root of 100, an irrational number approximately equal to 2.512, as most hand calculators will verify.
The human eye responds roughly logarithmically to light. For example, a star that is actually twice as bright as another, doesn't "look" twice as bright to the eye. A good example of this, may be noted at the time of a solar eclipse, when the Moon covers the sun's disk. It doesn't really seem to get dark until the sun is almost completely covered. When half of the disk is covered, and the light is cut by a factor of two, the difference in brightness is hardly noticeable.
A second notable accomplishment of Hipparchus was the discovery of precession of the equinoxes. This is the phenomena due to the gyroscopic wobble of the earth's axis that comes about because of the pull of the Moon on the equatorial bulge. As a result, the north pole of the celestial sphere performs a circular motion every 26,000 years with respect to the stars. At the time of Hipparchus, hardly more than 10 per cent of this period would have been available in recorded history. While Hipparchus lacked a physical understanding of the phenomena, he was able to describe the phenomena correctly as a westward motion of the equinoxes. This westward motion, called regression because it is opposite the motion of the sun, Moon, and planets.
It is finally worth noting that in spite of Hipparchus's obvious abilities, he adopted Aristotle's (384-322 BC) earth-centered model of what was then "the universe."
We can only speculate on why Hipparchus "regressed" to the Aristotilian view after Aristarchus had described the more correct picture. Some writers have suggested Aristarchus had not provided a mathematical model to predict celestial phenomena, while rudimentary methods, based on rotating crystal spheres were available. Others have suggested that it was already considered apocryphal to suggest the Earth was not the center of the universe. In that era, astrology was hardly separated from astronomy, and the astrologers hardly cared about the reality behind the orientation of the heavens. They only needed accurate positions.
Hipparchus introduced many of the methods of calculating planetary positions that were later refined by Ptolemy (85-165 AD), the last of our four ancient astronomers, and the only one born after the birth of Christ.
Ptolemy was also an Alexandrian Greek, and much of what we know of Hipparchus comes from his writings. His major work, the Almagest, gives the detailed mathematical methods by which the positions of the sun, Moon, and planets could be predicted. He did this with the help of a reasonably complicated model shown in Figure 8-1.
It is probably better for us to learn the correct model for planetary motion before trying to understanding Ptolemy's approximation to it. Briefly, what he did was move the Earth (E) slightly from the center of a circle, called the deferent. This violated the concept of a geocentric system, but apparently not enough to render it unacceptable. Planets (P) moved on small circles called epicycles. The centers of these epicycles (F) moved uniformly around an equant point, also, alas, slightly displaced from the center of the large circle.
When we discuss Kepler's laws, it will be clear why such a complicated construction as Figure 8-1 was necessary. Nevertheless, after a hundred or so years, the tables failed to predict planetary positions accurately, and at various intervals between the times of Ptolemy and Copernicus, planetary tables were reconstructed so that they fit the observed positions.
By the time of Copernicus, the "current" tables, which were constructed in the 1200's, with minor modifications another 200 years later, were no longer giving accurate positions. This was one of the motivations for Copernicus's work, but he also thought he had a simpler and more probably correct picture. He is the first of what we call the "pre-modern astronomers." We will be concerned with five of them:
Copernicus 1473 - 1543 Sun-centered universe Tycho 1546 - 1601 Accurate planetary positions used by Kepler Kepler 1571 - 1630 Laws of planetary motions Galileo 1564 - 1642 Jupiter's Moons, Sunspots, stars in Milky Way Newton 1642 - 1727 F = ma; Law of gravitation
It is important to remember only the relative sequence of these people and roughly when they lived. Copernicus came first; Kepler and Galileo were contemporaries. Newton was born the year (1642) the year Galileo died. Galileo was born the same year as Shakespeare, 1564. The other years you don't need to remember.
Planetary motion is hard to describe because the planets obey Kepler's laws:
Kepler's third law may be called harmonic because the ratio of the frequency of the root of a musical scale to the fifth is 2/3.
We will test Kepler's law of areas in an upcoming lab. We divide an ellipse in two, by constructing a perpendicular through one of the foci. What we will see, using The Sky is if the times for Mercury to sweep out these areas are in the same proportion as the areas themselves. This must be the case if Kepler's second law holds.
In the lab experiment, you will make estimates of times to sweep out areas. In general, there will always be errors associated with a measurement. Suppose the correct answer is 'y', and you get 'x' for the ratio of the two times. Then your relative error is:
y - x
-------- x 100 = error in per cent
y
People often ignore the sign in quoting a percentage error. So they may say I've made a 2% error or a 25% error, but not tell whether they were over or under the expected estimate. When you do the exercise, indicate the direction of your error.
Copernicus was born in northern Poland, of German parents. He studied law, medicine, and finally astronomy in Italy, before returning to Poland where he became a cannon in a cathedral at Frieburg, then in East Prussia. He was 30 years old. A decade later, he completed his new model universe. It had the sun at the center of the system, but used all circular orbits, and therefore could not accurately describe the Keplerian orbits without some fudging. But because it used a more nearly correct model than Ptolemy, the fudging was somewhat milder. Copernicus was a churchman by vocation, and concerned with the implication of his ideas. This may be why he only published his work, De revolutionibus at the end of his life. There is a story that he saw a bound copy of his book only as he lay on his deathbed.
Copernicus had a pretty good idea of the relative distances of the planets. He knew that if the planets went around the sun, their periods of revolution could not be directly observed from the earth.
For venus and mercury, you can get their relative distances from the sun without knowing their periods of revolution. All you need to do is find the angle the planet gets from the sun. At that point, the angle (earth-planet-sun) is 900, and the distance to the planet is just 1AU times the sine of that angle.
Distances to the exterior planets--only Mars, Jupiter, and Saturn were known--required the sidereal periods of those planets. The time for a planet to revolve about the sun with respect to the stars is called the sidereal period. Copernicus could find that with the help of what we call the synodic period.
Consider the earth, mars, and suppose that Mars is directly opposite the Earth from the sun. Astronomers call this configuration opposition. The synodic period of Mars is the time from one opposition to the next. It is the same from any definite configuration of these three bodies to the next, identical configuration. The synodic period of all celestial bodies are directly observed from the earth. The synodic period of the Moon, for example, is the time from full moon to full moon. It's the same on the average, from first quarter to first quarter, and so on.
We can get the (unobserved) sidereal period from the (observed) synodic period by considering relative angular velocity. Maybe it's easier to consider relative linear velocity first.
Suppose you have two carts, one going at speed V and a second with speed v, both in the same direction. For specificity, suppose V is greater than v. Then RELATIVE to the second cart, the first is going at a speed V - v, the difference in the two speeds. It's the same with the angular rates. The synodic rate is a rate of a planet RELATIVE to the earth, or the Earth relative to a planet. For the Earth and mars, for example, with sidereal periods P(earth) and P(mars), we have
360 360 360
------ = ------ - ----- (1)
Psyn P(earth) P(mars)
Or
1 1 1
----- = ----- - ------ (2)
Psyn 365.25 P(mars)
It's easier to remember the relations as a difference in rates. The higher rate comes first. For planets we write the synodic angular rate as the difference between the two sidereal rates. We always have to subtract the slower rate. For an inner planet, the earth's rate is slower; for an exterior planet, that planet's rate is slower. Thus for Mercury or Venus,
360 360 360
------ = ------- - ------ (3)
Psyn Psid 1 year
while for Mars, Jupiter, and Saturn,
360 360 360
------ = ------- - ------. (4)
Psyn 1 year Psid
You have to keep the units the same in each term, so if one period is in years, all of them have to be. You can cancel the 360's of course, since they appear in every term. Check the sidereal and synodic periods given in the following table:
sidereal period synodic period
(days)
Mercury 88.0 days 116
Venus 224.7 days 584
Mars 687.0 days 780
Jupiter 11.862 years 399
Saturn 29.457 years 378
The simplest way to find the distance to an exterior planet is to site at it at two times one sidereal period apart. Then you know the planet is in the same position with respect to the stars. The earth will be at two different positions, so you can triangulate and get the distance--again in terms of the distance of the Earth from the sun. That distance remained unknown for some time.
The relative position of the Earth in its orbit is known, because we know the earth's sidereal period. Observation of the planet gives its direction with respect to background stars. We make a scale drawing. We just draw a line from the two Earth positions, one sidereal period (of the planet) apart, and the planet will be where the lines cross.
Tycho Brahe, the second of the pre-modern astronomers was born a few years after Copernicus died. He was a Dane with a stormy character. His nose had been cut off in a duel, and he had a reconstruction made of gold, that can be seen in his portraits. He was perhaps the greatest of the naked eye observers--certainly, he was the last, great naked eye observer; the telescope was invented soon after his death.
Tycho's instruments were little more than arrangements like gun sights, attached to segments of a circle so that angles could be accurately measured. He measured the positions of stars and planets using a system of a small number fundamental stars. Their relative positions were generally good to somewhat better than a minute of arc (1/60 of a degree), an order of magnitude better than the ancients had done.
Tycho knew of Copernicus's system, of course, but rejected it. He was wrong, but one might say, for the right reasons. He argued that if the Earth moved about the sun as Copernicus suggested, that nearby stars should show a parallax, when viewed from different parts of the earth's orbit. This is illustrated in Figure 8-2.
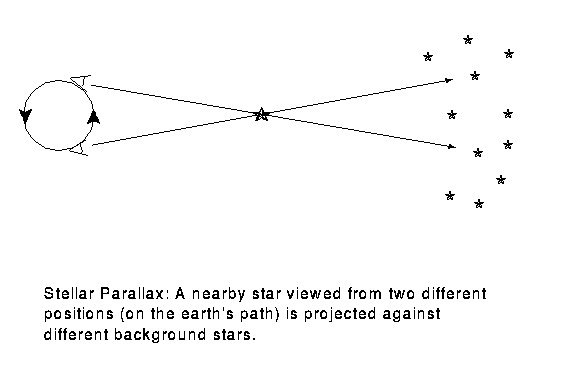
When Tycho failed to observe the parallax of any star, he invented his own system, in which the Earth was at the center, with the sun and the Moon revolving around it. However, in the Tyconic system, all the planets revolved about the sun. The relative motions were therefore the same as in the Copernican system, but since the earth did not move, there would be no stellar parallax.
Actually, the largest known parallax is slightly under a second of arc, too small to be measured without telescopic aid. This is one of many examples where a conclusion reached by application of the scientific method can be wrong.
Tycho had a falling out with his supporters in Denmark, and moved to Prague, where he met the brilliant young Kepler. They had their own stormy relationship until Tycho's bizarre death. The story goes that he was a guest at the table of the King, and could not leave the table to relieve himself as long as the King was there. His bladder burst.
Kepler then inherited Tycho's observational material, and with its help, discovered his laws of planetary motion. Kepler was truly bright, if a little crazy, and used ingenious ways map the positions of Mars within the solar system with the help only of it's angular position as seen from the earth. These methods are generally unimportant today, with one exception.
It turns out that the position of a planet with respect to the sun is a very complicated function of the time. Kepler was able to work out some quite simple relations that give this position precisely. One of the relations, still taught to any student of celestial or orbital mechanics is known as Kepler's equation.
Once Kepler had found that Mars obeyed his laws of motion, he could see that the motions of the other planets were consistent with them. It is arguable whether he might have used the measurements of Venus, for example, to obtain his laws.
Galileo and Kepler were contemporaries, but surprisingly, never met, and only had one exchange of letters. It is a mystery why this was so. Both enthusiastically embraced the Copernican system, and both were brilliant, well informed men.
Galileo reinvented the telescope after hearing that, and made a remarkable series of discoveries, ranging from sunspots and mountains on the moon to the four moons of Jupiter, called the Gallilean satellites in his honor. The motions of these moons about Jupiter resembled a miniature version of the Copernican solar system, and Galileo became convinced Copernicus had been right.
Unfortunately, Galileo lived near the seat of power of the Roman church, and he was sufficiently egotistical, or perhaps just unrealistic, to think that he could convince the churchmen of his position. He was called twice to Rome to be...corrected. During the first visit, he was given good advice by Cardinal Bellarmino, to discuss his ideas as a "model," rather than as reality. Had he done so, he might have avoided the second summons, after which he was put under house arrest. The hostility of the Roman Church to Galileo lasted into our own time.
Galileo and Newton laid the foundation of the science of physics as we know it. It is not a great exaggeration to say there was no physics before them. True, Archimedes reached important conclusions several centuries before the birth of Christ; the world was not ready to follow up on them.
While Galileo's discoveries were numerous, there was no unifying theme. Newton's contributions were of an entirely different nature. He was able to enunciate a minimal number of mathematical relations, which could account in quantitative terms for huge portions of natural phenomena. The mathematical edifice built by Newton was so powerful that toward the end of the nineteenth century, some physicists believed there was little more of their science to be discovered. This interesting view seems to be one that people get from time to time.
Newton's contribution to the understanding of the solar system were basically his laws of motion, and his law of gravity. We shall explore them more in the next lecture.
We discussed the ancient astronomers were Aristarchus, Eratosthenes, Hipparchus, and Ptolemy.
Aristarchus had a heliocentric model for the solar system; Eratosthenes measured the diameter of the earth. Hipparchus mapped bright stars of the sky, and discovered precession of the equinoxes. Ptolemy reverted to a geocentric model to keep track of the planets. His methods lasted until the time of the pre-moderns; Copernicus, Tycho, Kepler, and Galileo. Of the pre-moderns, only Tycho preserved the geocentric model because he could not observe parallax. Kepler's laws of planetary motion, and many of Galileo's discoveries were fit into the grand scheme of Newton's mechanics.
With the help of Newtonian mechanics, astronomers could predict the positions of planets, comets, and asteroids for time intervals that were limited only by the numerical precision of their calculations. Newton's laws made it clear that Kepler's were only an approximation, strictly true if there had been only one planet in orbit about the sun. In reality, the planets influence one another, even if slightly, so that Kepler's precise solutions, like the Ptolemaic projections, needed modification after a time. The important difference was that the reasons for the modifications were known, and they could be precisely taken into account.
In 1781, William Herschel discovered the first planet, Uranus, beyond those known to the ancients. Shortly thereafter, he discovered double stars, orbiting one another according to Newton's laws, thus demonstrating that the Law of Gravity was "universal." The first stellar parallax was announced by Wilhelm Bessel in 1838. It was then possible to determine distances to the nearest stars, and begin to probe the universe beyond the solar system.
According to Kepler's harmonic law, the planet's periods (P) and semi-major axes (a) obeyed the relation:
2
P
------- = 1 (1)
3
a
Now this relation holds rather closely for the planets, though not exactly, as we noted. But even within the restrictions of an approximation, the equation is only true if we count the period in years and the semi-major axes in astonomical units (AU). Kepler surely knew this. If you decide to stick with astronomical units, but measure the orbital periods in months, then the constant becomes (approximately) 144, or 122.
Now Galileo had measured the orbital periods of the satellites of Jupiter, and it is clear that the constant on the right side of Equation (1) was not unity for that system.
Galileo did not know the distance to Jupiter in miles, but he knew it terms of the AU, as did Copernicus. This same distance could also be computed from Equation (1), and the agreement was entirely satisfactory, or Kepler would never have formulated his harmonic law. With the distance to Jupiter known, the angular separation of its satellites from the planet suffice to give their distances--also in AU. One may use the skinny triangle relation to get the distances of the Jovian satellites from Jupiter itself.
With the periods and distances to these satellites known, one can see if they satisfy Equation (1). They fail to do this by a factor near 1000!
Newton was able to generalize Kepler's harmonic law with the help of his laws of motion and gravity. When his theory is applied it turns out that if a little mass m, like that of a planet, orbits a big mass M, like that of the sun, then
2 2
P 4 ------------- = ----------------------. (2)
3 G(M+m)
a
------------- = ----------------------. (2)
3 G(M+m)
a
The constant G is the number that tells how the two masses attract
one another in Newton's law of gravity. If they are separated by
a distance, d, then the force between them is
GMm
F = --------- (3)
2
d
The quantity force is precisely defined in Newton's mechanics, and
we will take up its definition in the next lecture. For the present,
we need to look carefully at Equation (2), and compare it with Kepler's
form, Equation (1). Apart from the numerical factor
4 2, the right hand of (2) contains the
constant of gravitation G, and the sum of the masses, M + m. Since
planetary masses are small with respect to the sun's mass, this sum
is dominated by the sun's mass, and is therefore nearly constant from
planet to planet. This is why Equation (1) works for the planets.
2, the right hand of (2) contains the
constant of gravitation G, and the sum of the masses, M + m. Since
planetary masses are small with respect to the sun's mass, this sum
is dominated by the sun's mass, and is therefore nearly constant from
planet to planet. This is why Equation (1) works for the planets.
When we come to Jupiter's moons, the big mass is no longer that of the sun, but that of Jupiter itself. The little mass, m, is that of the satellite. If these are small compared to Jupiter's mass, and it turns out they are, then (M + m) is essentially Jupiter's mass M. We now know that Jupiter's mass is about 1/1000 times that of the sun, and this explains the factor of 1000 between P2/a3 for the planets and for Jupiter's moons.
Did Galileo ever try to apply Kepler's harmonic law to Jupiter's moons? I know of no record that he did, but it certainly seems likely that he would try. If so, he would have quickly found the factor of 1000 discrepancy. What would he have made of it? Would he have thought the less of Kepler because of it? It really isn't known why Galileo never sought Kepler's advice or support. Kepler is said to have written twice to Galileo, but to have received only one reply. We may never know if the factor of 1000 in the harmonic law is relevant to this interesting historical puzzle.
Until the latter part of the nineteenth century, most astronomical endeavors were directed toward finding the positions of stars and planets, and where possible, accounting for them with the help of Newton's laws. Aside from measuring the positions, astronomers slowly improved their measurements of the brightnesses of objects, but until the new discipline of astrophysics, these measurements added little to our understanding of the universe around us.
In the late 1800's physicists and astronomers began to make new studies, based on the analysis of light with the aid of an instrument called the spectroscope. It had been known at least since the time of Newton that light could be dispersed into its constituent colors, but it was a century before methods of the systematic investigation of this effect could be explored in detail.
In 1861 the great German physicist Gustav Kirchhoff published the results of his quantitative analysis of the sun's spectrum, finding nearly two dozen chemical elements. Like Newton, he built on the shoulders of giants whose names we omit here. A few years later, the first measurement of the Doppler effect in starlight was made by the British astronomer William Huggins.
The advent of the analysis of the light from celestial objects focused attention on the mechanisms of the emission and absorption of light itself. These ultimately led to the quantum theory of matter, which provided the only accurate description of atoms and their structure.
Just as Newton had been very closely concerned with the motions of the planets, physicists concerned with properties of light were keenly interested in the spectrum of the sun and the stars. The name astrophysics was used to describe these new endeavors, and to set them apart from the old astronomy of position.
In the years near the turn of the century, astronomers probed the universe known to them, which we now recognize to be the sun's neighborhood in the Milky Way Galaxy. There were speculations that some of the fuzzy objects called spiral nebulae were distant stellar systems, but their nature wasn't really clarified until the 1920's.
At the end of the 19th century, and the beginning of the 20th, astronomers used the new tools available to them to explore the the universe beyond the solar system. Among these tools were the telescope and photographic plates, upon which stellar positions could be recorded and then measured with an accuracy sufficient to measure the parallaxes of stars to distances of perhaps 100 parsecs. This distance is minuscule when compared to even the size of our own Galaxy, which is tens of kiloparsecs across, but it is very large when compared to dimensions within our solar system. Remember that a parsec is 206265 AU!
In addition to parallaxes, astronomers had begun to measure the motions of stars, both across and in the direction of the line of sight. The former is called proper motion and the latter radial velocity.
Proper motions had been discovered in Newton's time by Halley (of comet fame), so by the end of the 19th century, these motions had been investigated with telescopic aid for several hundred years. Astronomers have traditionally assembled their observational results into large tables that they call "catalogues," and some of the most famous astronomers made use of a catalogue of proper motions published in 1910, which contained the motions of practically all of the naked-eye stars. With the help of this catalogue, astronomers discovered motion of the sun through the general star field as well as some systematic movements now known to be due to the rotation of the Galaxy.
Other astronomers had specialized the use of the spectroscope and later the spectrograph--with the spectrum recorded on a photographic plate--for the determination of radial velocities. The spectrometer, to use a general term, is the principle instrument of the new astrophysics, but it was actively used in the early 1900's to explore stellar movements in the neighborhood of the sun.
Unlike proper motions, radial velocities can be determined for distant objects, so long as they are bright enough. Moreover, one may get the radial velocity directly, in km/sec, for example while a proper motion only an angular displacement during some unit of time. In order to convert to km/sec, one must know the distance to a star. A disadvantage of radial velocities is that one obtains only one component of a star's motion, while with a proper motion, one obtains two.
Stellar motions and the positions of stars were keenly pursued in the first half of the 20th century, but they were gradually displaced at many observatories by the new astrophysics, with its emphasis on the structure, composition, and evolution of stars. In the second half of the 20th century, stellar astronomy in turn has been displaced by an emphasis on galaxies and the universe beyond our own Milky Way system.
Newton's laws of motion and gravity provided the basis for a (nearly) complete understanding of the motions of the planets. The century following, Newton's death was largely devoted to tracking known and newly discovered planets, and comets. In the 19th century astronomers took the first steps in exploring the universe beyond the solar system, with the measurement of the first parallax. Most of 18th and much of 19th century astronomy dealt with measurements of the positions of planets and stars. This astronomy of position was gradually displaced by the rise of astrophysics, primarily devoted to the chemical analysis of starlight with the help of the spectroscope.
Much of the universe studied by astronomers is quite hot. We have learned that the surface of the sun is some 6000K, and its interior is some 15,000,000K. These temperatures are typical of stars. At such temperatures, most bonds between atoms are broken, and very little chemistry is relevant. It is entirely different when we come to study the planets. As we well know, because we happen to live on one of them, planets can be the site of very complex chemistry. If we are to understand the structure and evolution of planets, we must consider the relevant chemical processes. In this lecture, we will review some of the principles necessary to understand the chemistry of the solar system.
Atoms are the smallest possible subdivisions of chemical elements. They are made up of positively charged nuclei surrounded by electrons. Virtually all of the mass of atoms is in the nuclei, while almost all of the volume is due to the electrons. Atoms are typically about 1 Angstrom (10-8 cm or 10-10 meter) in radius, while nuclear radii are some 10-13 cm. This difference in radii is about 5 orders of magnitude, it's huge. If you tried to draw a scale model of an atom, and drew a large circle on a piece of paper and put a dot in the center, the dot would be too big. Do you think you could see a dot drawn to scale with the naked eye? We'll leave this as a problem.
The nuclei are made of protons and neutrons. Only the protons have a net charge, but the neutron is only slightly more massive than the proton. Electrons carry the same amount of charge as the protons, but with the opposite sign. By convention, electrons are said to be negatively charged, and the protons positively charged.
If an atom loses an electron, it is called an ion. Any atom can have an ion, and the ion can have a net positive charge of one or more units, depending on how many electrons the atom loses. Neutral atoms, of course, have an equal number of protons and electrons. Atoms can also pick up one or more extra electrons. In this case they have a net negative charge, and are said to be negative ions.
The chemical element is determined by the number of protons in the nucleus. Atoms with the same number of protons, but different numbers of neutrons are called isotopes. Isotopes play a very important role in the chemistry of cosmic matter, but ordinary chemical processes are mostly governed by what the electrons do, so the isotopes have quite similar behavior.
Atoms combine to form molecules. A molecule is the smallest division of a chemical compound. The forces that hold atoms together in a molecule are called bonds. There are several kinds of chemical bonds which we will discuss shortly.
There are two great divisions in chemistry, organic
and inorganic. Quite a long time ago, organic chemistry
was thought to apply to reactions and compounds that could
only occur in living (or once-living) matter. As recently as
the early 1800's it was thought that some ``vital force'' that
only existed in living material was necessary to form organic
molecules. It was therefore a matter of some import, when
in 1828, the German chemist Friedrich Wohler synthesized the
organic chemical urea [CO(NH2)2] in
his laboratory from inorganic chemicals.
The periodic table is the key to much of chemistry. The version shown here we have colored some of the volatile elements blue. The involatile elements that are shown in red are all constituents of major minerals that make up the earth's mantle or crust. These minerals belong to three main families, known as the olivines (e.g. Mg2SiO4), the pyroxenes (e.g. Mg2Si2O6), and the feldspars (e.g. NaAlSi3O8). Iron occurs both in chemical combination with silicon and oxygen in the mantle and crust, but also in the core, where it is alloyed primarily with nickel. We discuss minerals in detail in Lecture 15. For the present, we merely note that the property of volatility is an important clue to the history of these minerals and the chemical elements from which they form.
To understand the periodic table, we need to know a few things. First, the atomic number Z increases by one unit from hydrogen through the heavy elements. Z is the number of electrons in the neutral atom or the number of protons in the nucleus.
The electrons come in shells and subshells. The n = 1 shell is called the K-shell. We don't need to know the names of the n=2, 3, 4, etc. shells. Subshells, also have names, involving the letters s, p, d, f, g, etc. There are also numbers (called l) associated with these letters. Further, the number of electrons that can be in a subshell is 2(2l+1):
s p d f g
l = 0 1 2 3 4
2(2l+1)= 2 6 10 14 18
The number of subshells in a shell increases with n. We can make a triangular scheme where we indicate the main shell by a number written before the letter that gives the subshell:
1s
2s 2p
3s 3p 3d
4s 4p 4d 4f
5s 5p 5d 5f 5g
6s 6p 6d 6f 6g 6h
The first period only involves the innermost shell, and it is completed with helium, which has 2 1s electrons, that is, two electrons in the 1s subshell. In this case (the K shell) the shell and the subshell are the same.
The next two periods fill both an s- and a p-subshell. Since there can be 6 electrons in a p-shell, there are 8 elements in these two periods.
The (4th and 5th) long periods in the periodic table have 18 elements. They involve s-electrons (2), p-electrons (6), and d-electrons (10), for a total of 18. But the filling order gets a little tricky. To remember it, draw arrows down through the triangles at angles from upper right to lower left, as done in class. The only trick is to get the angle right as you draw the arrows down. Fix this angle with the help of the first 3 periods, where you know you have to fill respectively: the 1s, then the 2s and 2p, and finally 3s and 3p. After that comes the 4s, but then the 3d comes before the 4p.
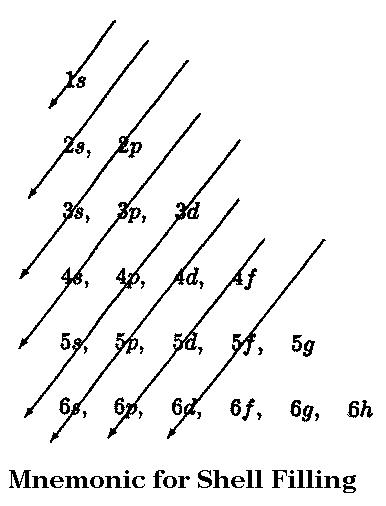
This triangular scheme is pretty neat, but it is not perfect. In the long periods, the filling doesn't go exactly in the order you would expect from the mnemonic. But the irregularities are mostly at the middle of the d shells, and won't concern us in this course.
In the 6th period, some monkey business happens. The 4f subshell fills, but there is no room for it on the main chart. The elements, cerium (Ce) through lutetium (Lu), 14 in all, are written below the main body of the chart. These elements are called lanthanides because they follow lanthanum. For historical reasons, they are also called rare earths. In the 7th period, an similar thing happens when the 5f subshell starts to fill. Again we get 14 extra elements, this time called actinides, because they follow actinium (Ac).
Chemical bonds between atoms are of two kinds, often called covalent and ionic. In both cases, the common denominator is the tendency for the molecule to create a closed, 8-electron outer shell about the two atoms. Covalent bonds achieve this by sharing electrons. Common molecules with bonds that are mostly covalent are the N2 and O2 of the atmosphere.
We may think of the bonding in simple inorganic compounds, like table salt (NaCl), as ionic. In these bonds, the electrons are transferred from one atom to another. Both atoms then become ions, with opposite charges. The number of electrons given up, or gained by an atom of a chemical element is called its valence or oxidation number. It can be positive or negative. By definition, oxidation means the loss of electrons. The opposite of oxidation is called reduction, and it means the gain of electrons. It's virtually always true that whenever something is oxidized, something else is reduced.
Refer again to a periodic table. A huge variety of educational resources for chemistry is now available on the internet. Try searching for "periodic table" or searching for words like "oxidation" or "chemical bond." You will find many links. The main problem is selecting something that is suitable for you!
The elements along the right hand column of the periodic table all have the ``desired,'' or completed, 8-electron shells. These elements are often called the noble gases because they do not react chemically with other elements---they are satisfied as they are. Elements in the next-to-last column, F, Cl, B, I, and At can borrow one electron and get the noble gas structure. They then become negative ions.
A standard example of ionic bonding is the compound NaCl, or sodium chloride---common table salt. Here, sodium from the first column of the periodic table, loses one electron to chlorine. The sodium ion, Na+ then has the stable neon structure, while Cl- has the electronic structure of argon. This is the general pattern followed in ionic bonding, although two or more electrons may be given up or accepted by atoms of an element.
Elements in the first column of the periodic table invariably try to lose one electron, and achieve the structure of the noble gas whose atomic number is one unit lower. Thus, so to speak, potassium, K, tries to become Ar, while Rb tries to become Kr. The elements in the second and third columns typically try to give up two or three electrons to achieve the noble gas structure. The oxidation numbers for elements in the first three columns of the periodic table are therefore pretty easy: +1, +2, or +3.
Toward the center of the periodic table, it becomes difficult to guess the oxidation number from the column. Many of these elements are filling an interior shell. For example, in the fourth period, the elements scandium through zinc are filling the 3d shell. Even in the case of the next-to-last period, the halogens (fluorine through astatine), can show a variety of oxidation numbers. Fluorine itself is usually -1, but the heavier halogens can have several oxidation numbers, depending on the atoms they combine with.
We will always assume that the element oxygen has an oxidation number of -2, and we can often use this to understand the oxidation states of other elements in a given compound once the formula is written. For any given chemical compound, the borrowing is always such that the total + and total - cancel, so the molecule (or crystal) is electrically neutral. The rule is the same for minerals as for inorganic molecules.
Sulfur may either gain two electrons and become like argon, or it may lose 6 electrons and become like neon. In the stinky gas H2S, it gains two electrons from the two hydrogens, so its oxidation number is -2. In a sulfate, like BaSO4, it has an oxidation number of +6.
Elaborate periodic tables, showing valences and much other useful information may be purchased from local bookstores for about a quarter. Or you may click on one of the elements in a "clickable" periodic table from the net. This will generally give you a variety of properties of the element, including the typical oxidation states.
Covalent bonds are seen in familiar molecules such as H2, O2 or N2. We can show their bonds either as lines or using dots:
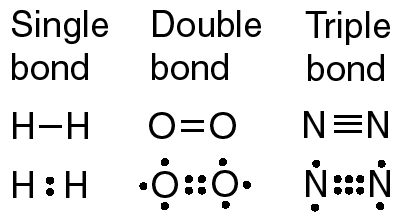
Generally, double bonds are stronger than single, but not twice as strong. Likewise, triple bonds are not 3 times the strength of singles, but they are stronger than double bonds. The N2 molecule is very stable, almost like an inert gas.
There are other kinds of weaker chemical bonds that are important especially for the liquid phase. One kind is known as the hydrogen bond, and the most common example perhaps, is in water. Here the region around the proton of hydrogen is positively charged, while the oxygen nucleus is negatively charged. This is because electron that belongs to the hydrogen is drawn by chemical forces toward the oxygen atom. The protons in one water molecule attract the oxygens from another. The hydrogen bond is one variety of bond that occurs as a result of a non-uniform distribution of charge over a molecule.
When molecules have a nonuniform distribution of charge, so that one end is permanently positive and the other negative, they are said to be polar. The configuration is called a dipole because there are two poles. The positive ends of polar molecules will always attract the negative ends of other polar molecules. Hydrogen bonding is a little stronger than many dipole bonds. It usually occurs between the hydrogen atoms in one molecule and either the oxygen or nitrogen atoms in another. Very long molecules can fold in such a way that hydrogen bonds can form between atoms of the same molecule. This is typical in proteins. Covalent bonds can also form between sulfur atoms in proteins. We'll get to this a little later.
Weak chemical bonds are especially important for life. DNA, for example, can be unzipped by enzymes and be copied by the mRNA because the strands are held together by hydrogen bonds. If the bonds were covalent, the DNA wouldn't be unzipped, and life as we know it would be impossible.
The molecular weight of water is only 18. Oxygen and Nitrogen molecules that make up the air have molecular weights of 32 and 28. Why are these molecules gaseous at room temperature while the much lighter water molecules are still liquid? The answer to this lies in the hydrogen bonds. These are illustrated in Figure 11-1.
Hydrogen bonds are indicated schematically in red between the large (O) and small (H) spheres.
We can get a rough estimate of the effective size of a complex of water molecules from boiling points. Simple hydrocarbons, with the general formula CH3(CH2)nCH3 have boiling temperatures lower than that of water until n is reasonably large. The boiling temperature of heptane (n=5) is 98C, and that of octane is 126C. Methane, CH4 boils at -57C. If we divide the molecular weight of heptane, 100 by that for water, 18, we conclude that between 5 and 6 H2O's tend to be stuck together in water.
The H2O molecule is common in the cosmos, but the liquid state is not. Gaseous water molecules are common in cooler stars, as well as in giant molecular clouds (Lecture 4). Ices of various kinds, including water ice probably form mantles of dust grains that are common in these clouds. Liquid water is really known only on the earth. There are speculations about pockets of subsurface liquid water on mars, in ancient comets, or in an interior ocean on the Jovian satellite Europa. Wherever liquid water occurs, life as we know it is at least possible. We shall return to this topic.
A good periodic table will have the atomic weights of the elements on it. For example, the atomic weight of iron is 55.87. This means that Avogadro's number of iron atoms would weigh 55.87 grams. Avogadro's number is approximately 6.022 x 1023. Avogadro's number of anything is called a mole. So a mole of iron atoms weight 55.87 grams.
Given the atomic weight of iron, it is easy to estimate the number of iron atoms in the earth's core, which has a mass of 1.9 x 1027 grams. The answer is
6.022 x 1023 (atoms/mole) x 1.9 x 1027 (grams) /55.9 (grams/mole) = 2.0 x 1049 (atoms).
The core not pure iron, but this gives us a rough idea of how many atoms of iron there are in it.
Molecular weights are calculated with the help of atomic weights. The molecular weight of water, H2O is equal to twice the atomic weight of hydrogen plus the atomic weight of oxygen. That's 2 x 1.008 + 15.999 = 18.015. In almost any calculation we'll do, 18 would be close enough.
How many molecules of water are in the oceans? An estimate of the mass of the oceans is 1.4 x 1024 grams. So there are some
6.022 x 1023 (mol/mole) x 1.4 x 1024 (grams) /18.0 (grams/mole) = 4.7 x 1046 (water molecules).
Why would an astronomer want to know the number of atoms of iron in the core? Well, the core of the Earth is slowly cooling. Indeed, the inner core is already known to be solidifying. This is a source of heat that must ultimately work its way out through the earth. How much heat is being released? We'll get around to an estimate of this eventually. One way to start is to estimate the relative energy states of iron atoms in the liquid and in the solid states. The iron atoms in the solid state can be thought of as having rolled into potential wells of the kind pictured in Figure 10-3. In so doing, they released energy in the form of heat. How much heat? Well, it depends on how many iron atoms there are. You can count the atoms, or the number of moles. Since we know Avogadro's number it's easy to get from one to the other.
How does the heat from the solidification of the core compare with other possible heat sources within the earth? Would the same sources be relevant on other planets? We will come to these matters in due time.
In ionic bonding, electrons are transferred from elements whose oxidation numbers are positive to those with negative oxidation numbers. In covalent bonding, electrons are shared. Weaker bonding, especially hydrogen bonding plays a key role in the chemistry of life. It accounts for the unique properties of water which make life possible.
We learned how to calculate atomic and molecular weights, and introduced the concept of the mole, and Avogadro's number.
There was nothing in the history of science to compare with Newtonian mechanics. Newton said his accomplishments were possible because he ``stood on the shoulders of giants.'' What he saw from this stance enabled him to make so sweeping a generalization about the laws of nature that it dominated physics for two centuries. He combined all of the laws of nature into terse generalizations, we now call Newton's laws. But his first and third law are actually contained in his second, if we interpret it properly. It is force equals mass times acceleration, or:
Before we can truly appreciate Newton's second law, we must consider the nature of the quantities involved, and how they may be defined. Newton's laws are like the axioms and postulates of mathematics, in that once they are accepted, we may use logic (and mathematics) to explore the consequences.
Mass, length, and time are called units or dimensions. But in Newton's mechanics, they are "undefined quantities" in the sense that we don't try to define them in terms of more fundamental things. It's impossible to avoid circularity if we try to define everything. The way this problem is avoided in mathematics, and in the deductive science of Newtonian mechanics, is by the use of undefined terms. In plane geometry, for example, points and lines are undefined.
We can give them "operational definitions" of mass, length, and time. For example, we may say how we measure them. Then time becomes what we measure with a clock, or length is what we measure with a ruler. Our science seems to work if we accept that these undefined terms can be understood and manipulated in a meaningful way. Now, with these, we can define precisely other quantities in quite a different way.
Velocity is defined as time-rate-of change-of position. If the velocity is constant, over a time t, then it is just a length divided by a time: v = l/t. It has units made up of the undefined quantities. For example v = 10 km/sec, means something goes 10 kilometers in one second. Unlike the definitions of mass, length, and time, the definition of velocity is mathematical, and precise.
Acceleration is time-rate-of-change of velocity. If a car starts at zero velocity and accelerates uniformly to velocity v in time t, then a = v/t. The units of a are length divided by time SQUARED. For example, the acceleration of gravity at the earth's surface, little g, is 32 feet per second per second or 32 feet/sec2. Again, the definition is mathematical and precise. In cgs units g = 980 cm/sec2.
Momentum is mass times velocity. Again an exact definition that ultimately breaks down to the undefined quantities mass, length, and time. An important concept, angular momentum, will be discussed a little later.
Energy is the ability to do work. Work, we define as a force times a distance. So energy has the units of force times distance or mass x length2/time2. These are the same units as mass x velocity2.
Energy is a powerful concept in our understanding of the world we live in. It comes in many different forms, and much of what we observe in our world involves the transformation of one form of energy into another. We can even understand much of how the microscopic world behaves in terms of the interplay of kinetic and potential energy. These will be discussed shortly.
We said that mass, length, and time could have "operational definitions." The American physicist Percy Bridgeman (1882-1961) talked about operational meaning in a broader sense. To him, a question had operational meaning if there were a way to perform an operation to get at the answer. If I ask how much the classroom eraser weighs, this question has operational meaning, because we can put the eraser on scales and find the answer. If we ask what is beyond the edge of the universe, it is harder to think of any way to answer that question. So for Bridgeman, that would be an operationally meaningless question. Likewise, you might ask what existed before the Big Bang. Again, it is hard to figure out how one might answer this question, so it may be called meaningless in the sense Bridgeman posed.
Other questions might involve one's aesthetic judgement. Who is the better tenor, Domingo or Pavarotti? This question might or might not be operationally meaningless, depending on what we might agree on for an operation to answer it. Should we take a poll? Aesthetic questions may be meaningless in the Bridgeman sense, but still fun to ask and debate.
Newtonian physics is deterministic. Given the positions and velocities of all of the particles in the universe, Newton has a recipe for calculating all future positions. Everything is determined--but only in principle. This was mentioned briefly in Lecture 3. There is only a small class of problems that can be solved in detail so that we can do predictions of the behavior of the system for all time. One of these is the two-body problem, the sun and one planet. For this, we can get a solution that will be valid for all time.
As soon as you add a third body, such as the sun, the earth, and the moon, we have the notorious three-body problem, for which there is no known solution that can be written in closed form. Such problems must be attacked by numerical means. We say that "in principle" we can get answers that are as accurate as we want, but in practice, numerical inaccuracies enter, and the further we get from the starting point, the less accurately we can predict what is going to happen.
Computers have made great advances possible in predicting the way multiple bodies will interact gravitationally with one another. But we can still only say that we can get the answers for the distant future "in principle."
Quantities like displacements, velocity, and acceleration, are called vectors. A vector is often defined as a quantity with both magnitude and direction. Velocity, for example, surely has both. If you are driving a car it might have the direction `north' and the magnitude 60 miles an hour.
We can think of vectors as arrows, where the length of the arrow stands for the magnitude of the vector, and the direction corresponding to the vector is the direction of the arrow. We'll use square brackets here to indicate vector quantities. So if [a] and [b] are two vectors, we can take their sum or their difference. To get the sum, put the tail of [b] at the head of [a] and draw the resultant vector, say [c] = [a] + [b] from the tail of [a] to the head of [b].
Likewise, we can subtract [b] from [a] by reversing the direction of [b] and adding it to [a].
Let us investigate what happens if we drop something. It falls under the action of gravity, which at the surface of the earth, is approximately constant. Remember that velocity = d/t and acceleration = V/t. Both of these relations are simplified. In each case, we assume the time is zero at the start, and after the time t the distance is d, or the velocity is V. On the left, we assume a constant velocity, and on the right, a constant acceleration. Clearly for a constant acceleration, the velocity must change. Let us see how much it changes for a falling body.
distance velocity
d ^ x V ^ *
| x | *
| x | *
| x | *
| x | *
| x | *
| x | *
0 ------------------> time 0 ----------------------> time
0 t 0 t
When a body falls from a distance d above some surface, it does so with a constant acceleration. If the velocity it reaches at the end of the fall is V, then the average velocity for the time t is V/2. So we have
d = (V/2)t (3)
The acceleration of a falling body is traditionally called little 'g'. It is 32 feet per second per second. Since it is a constant, the velocity after a time t is
V = gt (4)
If we substitute for V in (3) using (4), we get the famous falling body law, known to Galileo:
2
d = (1/2)gt (5)
Now let us calculate the work done in raising a mass 'm' a distance 'd' against gravity. The work is the force times the distance. The force is mass times acceleration, m times g. So
Work = m g d = energy after the lift. (6)
When the mass m has fallen by the distance d, its velocity is given by (4). In equation (6), put (5) in for the distance, and use t = V/g from (4), we get
2 2 m g d = m g (1/2)g (V/g) = (1/2)mV (7)
The left-hand side of (7) represents potential energy, and the right-hand side kinetic energy, or energy of motion. Together, they demonstrate conservation of energy. This law actually transcends Newton's laws, and is valid in domains where Newton's laws break down. Because of the conservation of energy it is possible for us to keep track of energy as it undergoes various transformations.
As we raise a the weight, we do work against the gravitational field of the earth, and give the mass potential energy. As the mass falls, this potential energy turns into kinetic energy. This happens in such a way as to keep the total energy constant--conservation of energy.
We can use this simple thought demonstration to illustrate one more concept. It is useful to make plots of potential energy as a function of position. In the figure on the left below, we plot potential energy for a mass lifted in the (nearly) constant gravity at the earth's surface. On the right, we illustrate the potential energy for a planet of mass 'm' in the variable force field of the sun.
Potential Potential
energy Energy -----------------------> zero
PE ^ x PE ^ *
| x | *
| x | *
| x | *
| x | *
| x | *
| x | *
0 ------------------> dist. ----------------------> time
0 d 0 r
The potential energy of the planet derives from the inverse-square force due to Newton's law of gravitation: F = -GmM/d2. It is often useful to use a minus sign in this force law to show that the force increases as d decreases. Usually this won't be critical for us. One can derive the expression for the potential energy from this relation with some simple calculus, but here, we just write down the answer: PE = -GMm/r. This will have to be good enough for us for the present. You can see that when r is infinity, PE will go to zero. This is indicated by the arrow pointing to the word "zero."
The concept of potential energy, and the potential energy curve are very important, and we will see much more of them.
From Newton's second law, F= ma, we can see that the units of force are those of a mass x and acceleration, or a mass times length divided by time2. If we use SI units, then we have force with units kilograms x meters x sec-2. Astronomers like cgs units, for centimeter-gram-seconds. Here force has units of gm x cm x sec-2.
Since work is a form of energy, and work is a force times a distance, the units of energy are those of force x length. The SI unit of energy is called the Joule, while the cgs unit is called the erg:
1 Joule = 1 kg x 1 meter2/1 sec2
1 erg = 1 gm x 1 cm2/1 sec2
There are 107 ergs in a Joule. Energy appears in so many forms that other units are more convenient than the erg and the Joule. The energy levels of atoms are separated by energy steps of the order of a unit called the electron volt, or eV. The name comes from the fact that if an electron falls through an electrical potential drop of one volt, it will gain 1 eV of energy.
1 ev = 1.602 x 10-12 erg
Atomic nuclei also have energy levels, but they are typically a million times greater than an electron volt. When discussing the energies associated with atomic nuclei, it is convenient to use the million electron volt unit, of MeV.
1 Mev = 106 eV
We will have occasion to introduce other energy units later in the course, such as the kiloton of TNT, the British Thermal Unit, and the equivalent of a barrel of oil. All of these units are readily converted from one to the other by simple multiplication.
Let us consider what is called the two-body problem. We have a planet with a very small mass in orbit about a massive body like the sun. To a first approximation we may assume the sun is stationary and just consider the planet's motion. This motion takes place in a plane. Think of an arrow pointing from the sun to the planet. We'll call that the planet's radius vector. The velocity vector points wherever the planet is going. These two vectors define a plane. The force between the sun and the planet is always along the radius vector, and therefore always in the same plane. So there is nothing to force the planet out of that plane. Two- body motion is always in a plane.
we may call the two components of the planet's velocity vr and vt. The `r' can stand for `radial' and the `t' for tangential. We add them using the Pythagorean Theorem, so the total velocity v obeys
2 2 2
v = (v ) + (v ) (8)
r t
The kinetic energy is just (1/2)mv2, with v2 given by (8). Now consider the potential energy of the two-body problem which we discussed in connection with Figure 11-2(b). We take the zero of potential energy when the two bodies are at infinite separation, that is as r --> infinity. For any finite r, then PE is negative, and it gets more negative the smaller r is. We stated, but did not prove the potential energy has the form
GMm
PE = - ------- . (9)
r
This looks just like the force law except for the power of r, which is squared in the force law (GMm/r2). We use a negative sign with the force law to indicate the force is directed toward smaller r. Equation (2) shows that the PE has the dimensions of a force times a distance, and that means an energy.
The potential curve going down to minus infinity for arbitrarily small r describes the situation where we drop a planet right "at" the sun. Then the planet would fall straight toward the sun and would eventually hit it. If we push the planet toward the sun, but not exactly "at" it, the nature of the problem changes because we have added ANGULAR MOMENTUM to the problem. Angular momentum is the product
l = m v r. (10)
t
The letter 'l' (lower case ell) is a common designation for angular
momentum. In the two body problem, this L is a constant of the
motion. It is easy to show that it's constancy is very close to
Kepler's law of areas, but we won't do here. Just take my
word for it, this L is constant for the two-body problem.
Now, let's diddle again with the conservation of energy. We have
1 2 2 GMm
- m[(v ) + (v ) ] - --- = E. (11)
2 r t r
This states that the kinetic plus the potential energy is a constant, which we call E. With the help of (10) we can eliminate vt from (11). We just put vt = l/mr into (11). Then put the term with the `l' on the right along with the potential energy term.
2
1 2 GMm 1 l
- m(v ) = E - [ - ----- + - m -------- ] (12)
2 r r 2 2
(mr)
We need to reinterpret Equation (12). The left-hand side looks like the kinetic energy for motion in one dimension. Look again at Equation (7). We take (12) as describing the kinetic energy (KE) for motion in the r-direction only. If E is the total energy, and PE is the potential energy, we know E = KE + PE, or KE = E - PE. Equation (12) gives the kinetic energy of motion in the r-direction in terms of the total energy and a new kind of potential energy term, which the physicists call the "effective potential energy" for r-motion only. We shall call it "EPE." EPE and PE have the same units, energy.
2
GMm 1 L
EPE = [ - ----- + - m -------- ] (13)
r 2 2
(mr)
With the help of constancy of the angular momentum, we have eliminated the velocity in the tangential (often called theta) direction. The motion in r behaves like a real one dimensional system, except the potential is (13) instead of just the -GMm/r. How does that change the potential curve?
The EPE has only the variables r and r2. All other terms are constant. Compare the properties of r and r2. We know that r2 gets big faster than r. When r is 10, r2 is 100, and so on. Similarly, r2 gets SMALLER faster than r. When r is 0.1, r2 is 0.01, and so on. If you think about this in connection with (13), you will see that the first term on the right will be important for large r and the second one for small r.
EPE
^
|*
0 - |--------------------------------------> r
|* *
|* *
| * *
| *<--------------->*
| * *
| * *
| * *
* *
* *
* *
Fix this shape in your memory, because it appears in other contexts than just planetary motion. Way off on the right, the curve will approach EPE = 0 more and more closely. The technical term is an asymptotic approach. We'll just say EPE is zero at r = infinity.
Let us now try to describe one dimensional motion under a potential curve such as that shown in Figure 11-3. It would behave just like a block sliding with no friction on a surface of that shape, or a bead moving on a wire bent into that shape under the action of simple gravity.
If the bead starts from far on the right, at EPE = zero, it will slide to the left, and come to a halt at small r also at EPE = zero. Then it has enough potential energy to reverse its trajectory and go all the way off to r = infinity again.
A real bead on a wire wouldn't do this because of friction. Common sense tells you the bead would end up at the bottom of the curve. This would happen in the two-body problem also, if there were some way for the incoming planet to lose energy. It might lose energy as a result of interaction with a third body, but in the solar system, this isn't so likely.
What this means is that in the two body problem, you can't get a finite elliptical orbit for an object like a planet or comet that falls in from infinity. There is always enough kinetic energy to take it out to infinity again. At small r, the r-component of the velocity has come to zero, but the tangential velocity-component gets very big, by the law of areas.
Consider Keplerian motion in the context of the modified potential curve. The value of r changes from a minimum, called perihelion to a maximum, called aphelion. That is like having a bead sliding back and forth inside the potential curve. The inner and outer extent for the stable orbit are indicated on Figure 11-3 above by the arrow. Oscillations of the bead would be in the "bowl," below this line.
To get a stable orbit, a body falling in from infinity must lose energy somehow. Conversely, for a body to be thrown from a stable orbit, it must gain energy. In the solar system, there are numerous bodies, and it is thought that Jupiter's interactions have thrown out many smaller bodies from the inner solar system. This doesn't happen very often, but over a long period of time some important effects can occur.
In Lecture 35 we will discuss the possibility that the comets in the Oort cloud (cf. Lecture 4) were ejected from the inner solar system.
The concepts of gain and loss of energy, stable orbits, and interactions with external systems to supply or subtract energy apply to atomic and molecular systems as well as planets. We shall meet them again, along with the general shape of Figure 11-3.
We have used the word "pressure" many times in the previous lectures. Most of us have a qualitative idea of what the word means. We say the atmospheric pressure is higher at sea level than on the top of a mountain, and higher inside an inflated tire than outside of it. We can be more precise.
We can define pressure as a force per unit area. Let's give some examples. Suppose a person weighing 50 kilograms steps on a square board that is 20 cm x 20 cm. The force (F) the man exerts is his mass (50 kg or 5000 gm) times the acceleration of gravity (980 cm/sec2). Thus F = 4.9 x 106 dynes, and the pressure on the 20x20 board is 1.23 x 104 dynes/cm2. What pressure would the person exert if the board were 40 cm x 40 cm? Clearly, it would be a factor of 4 less, or 3.06 x 103 dynes/cm2.
How does one figure the pressure of a gas, say inside a sealed room or an automobile tire. One way is to assume the pressure is the same everywhere within the volume, and ask what the force is on a unit area of the wall.
If you are in a typical room at the Earth's surface, you know that the pressure is 1 atmosphere, which in cgs units is about a million dynes/cm2. The pressure exists within the gas inside the room, even though there is no wall or surface for one to use to measure the force. How can this be?
The pressure within a gas derives from the motions of the gas molecules. The pressure (P) in most gases of interest to us are described by the ideal gas law, P = (n/V)RT. Here, 'n' is the number of moles of gas in a given volume V, T is the temperature in Kelvins, and R is the gas constant. If the gas in a room is uniform, then n/V and T will be the same at every point, so the pressure is defined within the room, as well as at the walls. We must leave it to physics or chemistry courses to show that this pressure could be related to the force that would be exerted on a unit surface, anywhere in the room.
It might be useful at this point, to review the section in Lecture 6 on the solar interior.
Newton's mechanics forms a deductive scheme based on the postulates of his laws and the undefined quantities mass, length, and time. From them we define other useful dynamical quantities, velocity, acceleration, momentum, force, and energy. All but the latter of these derived quantities are vectors--they have both a magnitude, and a direction. Energy may appear in the kinetic or potential form. In the gravitational problems, such as the two-body problem, we take the zero of potential energy to be when the two objects are separated to infinity. For finite separations the potential energy is therefore negative. Classical motion may often be pictured with the help of potential curves. In the two-body problem, the total energy and angular momentum remain constant. A third body can influence either of these constants.
We defined pressure as a force per unit area, and described how it may be defined at any point within an ideal gas.