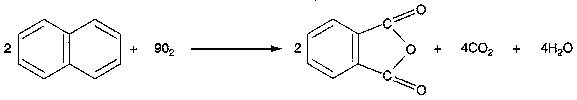
Oxidation of Naphthalene to Phthalic Anhydride
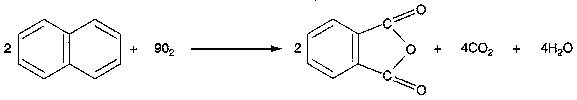
![]()
The oxidation is to be carried out in a packed bed reactor with cooling. The ambient temperature is constant along the length of the reactor. The pressure is 1 atm and the partial pressure of naphthalene is varied between 0.01 atm and 0.02 atm. The entering temperature is varied between 600 and 675.
a) Starting with the nomenclature and the mole balances in the text, write the mole balances in the form given by VanWelseneare and Froment [CES 25 p1503 (1970)].
b) Starting with the nomenclature and the energy balances given in the text, write the energy balance in the form given by VanWelseneare and Froment.
c) For each of the conditions in part (b), make a phase plane plot to include the critical trajectories for
1) Locus of maximum concentrations CAm vs. T
2) Locus of inflection point concentrations CAi(1) and CAi(2) vs. T
d) Plot the partial pressure and temperature profile for
1) T0 = 600 , Ta = 600 , Pi0 = 0.017 atm
2) T0 = 625 , Ta = 625 , Pi0 = 0.017 atm
3) T0 = 625 , Ta = 625 , Pi0 = 0.01825 atm
4) T0 = 625 , Ta = 625 , Pi0 = 0.0185 atm
a) Put the mole balance equation in form used by VanWelseneare, i.e.
Starting with the Mole Balance
![]()
The rate law is
![]()
Combine rate law and mole balance
b) Put the energy balance in the form used by VanWelseneare
Starting
from the basic energy balance
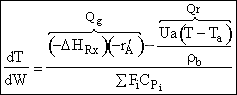
Parameter Values
Gas density:
![]()
![]()
Catalyst bulk density:
![]()
Entering gas velocity:
![]()
Specific reaction rate:
![]()
Overall heat transfer coefficients:
![]()
Radius of pipe:
![]()
Entering partial pressure of O2 (B) [X.S.O2]:
![]()
![]()
Evaluating
the parameters A, B, and C.
![]()
![]()
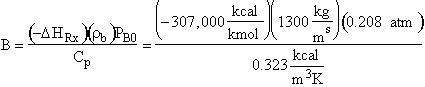
![]()
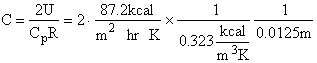
![]()
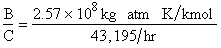
![]()
![]()
![]()
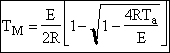
c) Calculate the locus of the maximum,
![]()
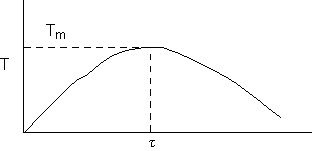
At the maximum, Tm
![]()
at max PA = Pm
![]()
At the inflection point
 at T = Ti,
PA
= Pi
at T = Ti,
PA
= Pi
The equations for the inflection points are
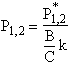
The equations for the inflection points are
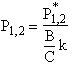
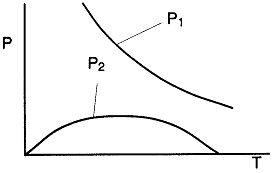
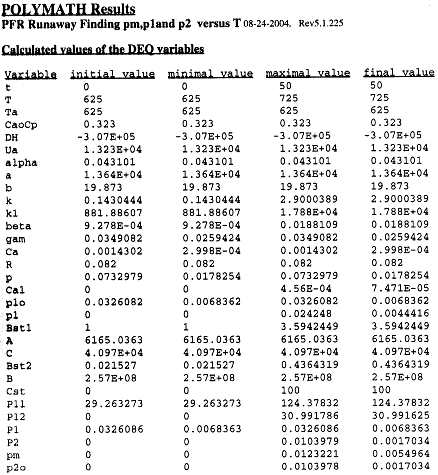
Table R8.2-1. Finding Pm, P1, and P2 as a Function of Temperature

![]()
The Polymath program to calculate the trajectories is shown in Table R8.2-2.
Table R8.2-2. Trajectories for Runaway
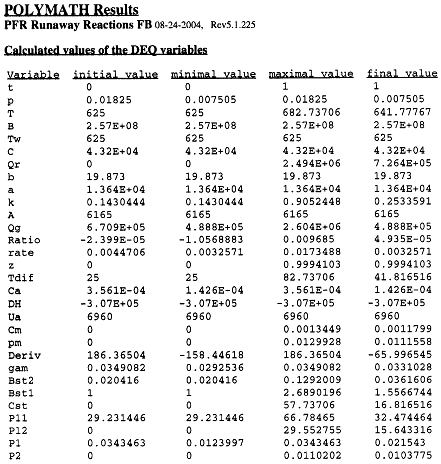
Inflection Points
P1=Pi1

Inflection Points
P1=Pi1
P2=Pi2
d) We will now increase PA0 from a stable 0.017 atm to 0.0185 atm where runaway will occur.
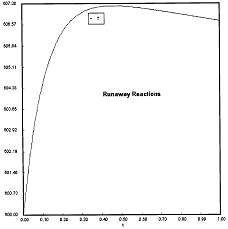
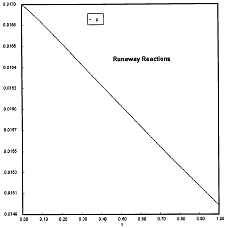
Criteria 1 is not exceeded.
Reaction Conditions: T0 = Tw = 600K , PA = 0.017 atm
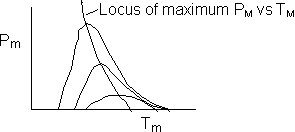
We are far from runaway. The intersection of the PA vs. T trajectory with Pm vs.
Tm is no where near the maximum. Very little conversion at these conditions ![]() . Now increase the temperature to 625°K.
. Now increase the temperature to 625°K.
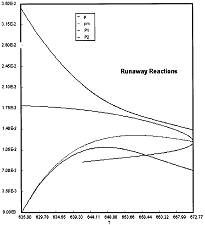
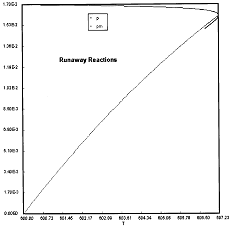
Runaway Criteria 1 exceeded, but Criteria 2 is not exceeded.
Reaction Conditions: T0 = Tw = 625K , PA0 = 0.018 atm
Here we are at (approximately) criteria 1 the PA vs. T trajectory intersects the Pm vs. Tm curve near the maximum.
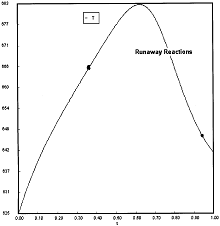
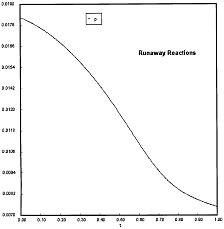
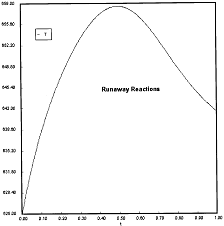
At PA0=0.01825 atm we are at the oneset of Runaway.
Reaction Conditions: T0 = Tw = 625K , P = 0.01825 atm
One notes that we are at the onset of runaway. The PA vs. T trajectory is tangent to the inflection point curve (criteria 2).
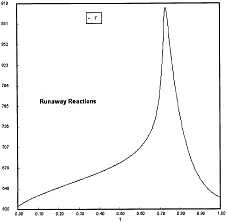
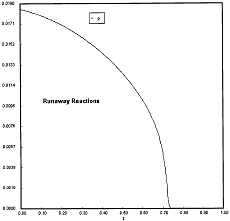
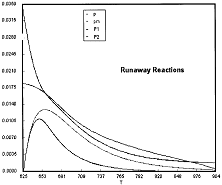
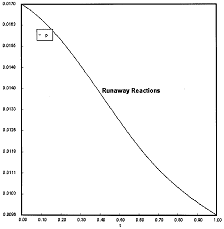
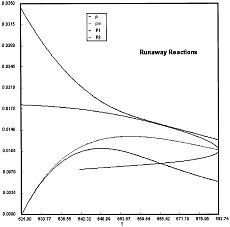
Runaway has occured.
Reaction Conditions: T0 = Tw = 625K , P = 0.0185 atm
Runaway occurs when we increased the entering partial pressure ever so slightly from 0.01.
Back to Runaway Reactions in PFRs