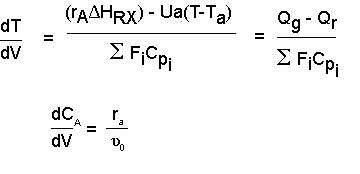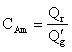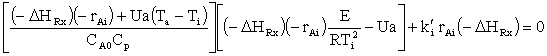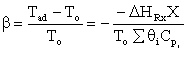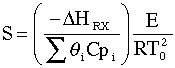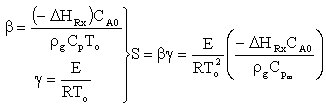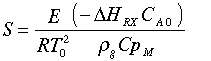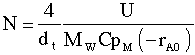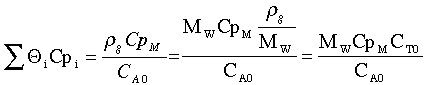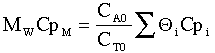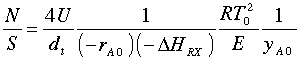Phase Plane Plots
We transform the above temperature and concentration profiles into a phase plane in the following manner.

(1)
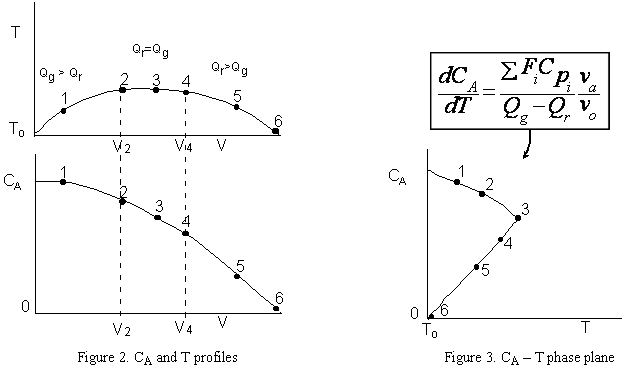
(2)First, we obtain the temperature and concentration profiles and then use these to obtain the phase plane plot of CA vs. T.
For example, at volume V2 the temperature is T2 and the concentration is CA2.
Now increase the entering concentration CA0. Increasing A0 will increase the reaction rate.
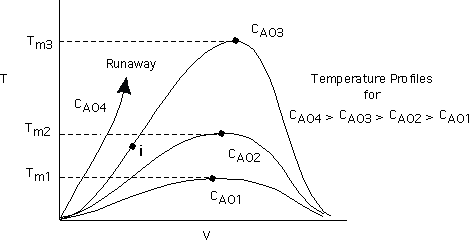
Figure 4. Temperature profiles
Note: We observe an inflection point, i, in the curve for CA03 . Also note the maximum temperature for each of the concentrations, i.e. Tm1, Tm2 and Tm3. We now look at the concentration profiles for each of these entering concentrations.
Figure 5. Concentration profiles for different values of CA0.
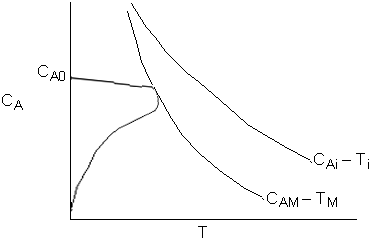
Again, forming a phase plane plot of CA vs. T

Now let's plot the maximum temperature for each entering concentration, CA0, and the corresponding reactor concentration CAm at this maximum temperature, Tm.

Figure 4 shows the temperature profile for three different entering concentrations [CA03 > CA02 > CA01]. Figure 5 shows the concentration profiles for the same set of entering concentrations. Figure 7 shows a phase plot of CAm as a function of Tm. This plot (Figure 7) could also have been obtained directly from the equation
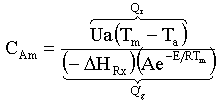
(3)
If Tm is above the TM (the temperature at which CAm is at its maximum value) then
(4) The term Q'g increases more rapidly than the heat generated "prime" (It's "prime" because it does not include CA). In other words the rate of increase of temperature dependent part of Qg is greater than the rate of increase of the temperature dependent part of the heat of removal, Qr.
The following figure shows a plot of CAm vs. Tm for different ambient temperatures (To≡ Tw)
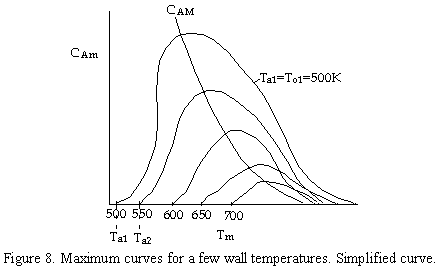
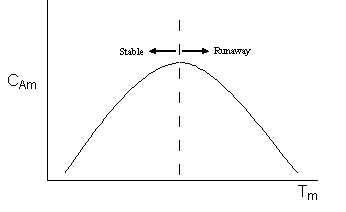
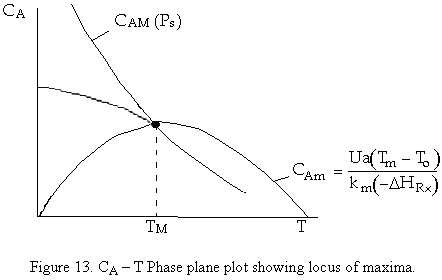
We note that the concentration CAm goes through a maximum as the temperature Tm is varied. Different values of this maximum result for different values of Ta (Tw). The line CAM is the locus through these maximum values.
We want to see how the concentration of A at the maximum temperature CAm varies with the maximum temperature Tm. Specifically we want to find the maximum value of CAm and the corresponding temperature Tm.
(5)
(6)
Substituting Equation 6 into Equation 5 and simplifying yields:
(7)
(8)
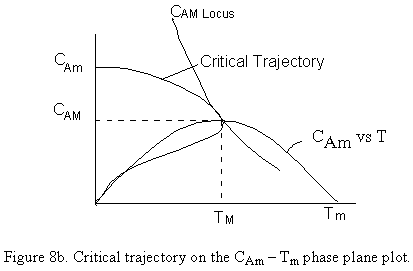
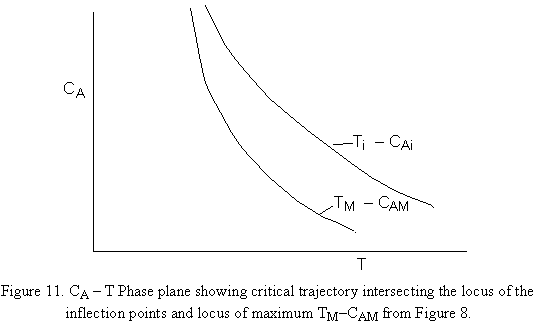
- Criteria 1 - Criteria Based on the Critical Trajectory, CM versus TM. The trajectory going through the maximum of the "maxima curve" is considered critical and therefore is the locus of the critical inlet conditions for CA and T corresponding to a given wall temperature. That is, the trajector whose maximum point crosses the CAM verse TM curve will be considered as runaway. Note this is a conservative criteria.
To calculate the CAM vs. T Curve
- Choose Ta
- Calculate TM
- Calculate kM
- Calculate CAM
The critical trajectory goes through Tm. The locus of the maximum CAM from Figure 8 is also shown on this figure. What is the inlet concentration that is related to this critical trajectory? The safe inlet concentration can be found by using adiabatic conditions.
(9)
(10)
(11)
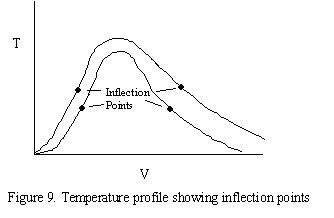
Criteria 2 - Criteria Based on Inflection Points
We will now derive a second criteria related to the inflection point on the Temperature profile. We are going to derive an equation for the locus of inflection points as a function of Ta. To simplify manipulations in the derivation, we are going to set To=Ta.
Starting with Equation 1, Let
At the inflection point
Then Equation 1 can be rewritten as
(12)
Differentiating Equation 12
Differential ting (-rA) and the using equation 12, we arrive at
If we have a first order reaction
then we can solve this equation to find CAi as a function of Ti to find the locus of the inflection points.
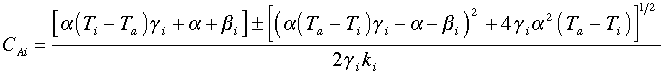
- Criteria 2. Runaway will occur when the trajectory starting at CA0 and To intersects the locus of the inflection points.
So how far do we back off from the inflection point conditions 10?C, 0.1 mole/dm3? These are arbitrarily set numbers (e.g., 10?C) and we need a criterion based on the intrinsic properties of the system and not on arbitrarily limited temperature range. Therefore use the locus of CAM as a function of TM.
Why use locus of maximum, CAM vs. TM?
You want to stay away from the intersection of the CA/T trajectory and the locus of the inflection points.
Criteria 2A. (Conservative Criteria) Runaway will occur if the trajectory starting at CA0 and To intersects the locus of the maxima of CAM and TM for different values of To (i.e. Tw because To = Ta = Tw) (See Figure 5)
- Criteria 3
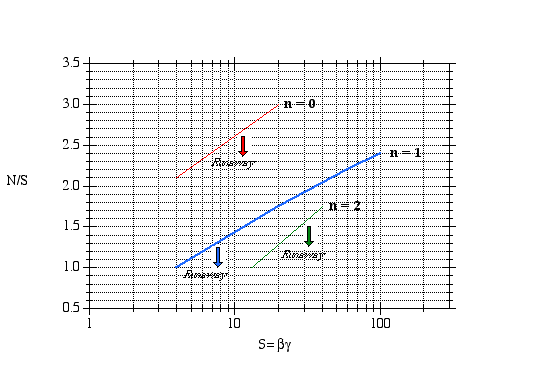
Runaway reaction figure adapted from Gilbert F. Froment and Kenneth B. Bischoff, Chemical Reactor Analysis and Design, John Wiley and Sons (1990). A number of computer experiments were carried out to determine runaway in a PFR. The results were quantified using two parameters, S and N. The parameter S is the product of the dimensionless activation energy, g, and the dimensionless adiabatic temperature rise, b.
C 3.1 C 3.2
The dimensionless activation energy is
C 3.3
Approximations and errors in the original article.
Comparing the term multiplying
in Froment and Bischoff (Eqn 11.5.2-2) on page 408 with Fogler (Eqn 8-56)
on page 459 for DCP = 0
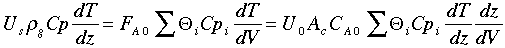

Equating the coefficient of
.
C 3.4 therefore equating Froment and Bischoff with Fogler,
C3.5 Froment and Bischoff
C 3.6 (1) The other parameter N given in Froment and Bischoff is
C 3.7 (2) Use equation C3.7 for liquids. For gasses we again equate the heat capacities:
C 3.8 (3) C 3.9


Note: The equation for (N/S) in Froment and Bischoff is not correct. If you check the units you will find (N/S) is not dimensionless.
where
rg
= Gas density (kg/m3)
Mm
= Mean molecular weight (kg/kmol)
dt
= Tube diameter (m)
CT
= Total concentration (kmol/m3)
CA0
= Entering concentration of A (kmol/m3)
U
= Overall heat transfer coefficient (J/m2 • s • K)
CPi
= Heat capacity (kJ/mol•K)
Mm
= Mean molecular weight (Daltons)
CPm
= Mean Heat capacity on a per mass basis (J/kg•K)
R
= Gas constant (J/mol•K)
E
= Activation energy (J/mol)
-rA0
= Rate of reaction (mol/s• m3) at To,
DHRx
= Heat of Reaction (J/mol)
To
= Temperature (K) (To = Tw = Ta)
no
= reaction order
Figure 11. Runaway diagram** (Adapted from G.F. Froment and K.B. Bischoff, Chemical Reactor Analysis and Design, 2nd ed. New York: John Wiley and Sons,1990).**You will want to use the original graph in either Froment and Bishoff or in the original article as this reproduction is only approximate. Also remember that these calculations were carried out for Ta=T0.
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering.