Challenge - Solution

In order to come up with the final graph that models the behavior of CO ppm in the South California Air Basin, we must first program come up with a block diagram model which represents the three counties as a group of PFRs in series.

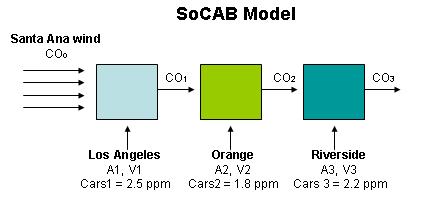
From this proposed model, we will program a set of equations in Polymath, which will vary in comparison to the original case (Problem). The difference consists in that there will be three sets of differential equations, and that each county will have its own vehicular flow, intensity of CO emissions, and initial concentracion of pollutants in the atmosphere. Consider the following image:

Solving the proposed problem on Polymath, the graph of the three counties over a period of 72 h resulted in the following image:

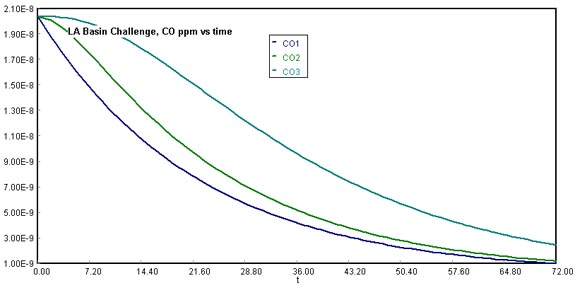
CO1 represents the concentration of carbon monoxide in the Los Angeles County. CO2 represents the same concentration as the Santa Ana wind leaves L.A. and blows into Orange County. CO3 represents the levels of CO accumulated in Riverside County until the Santa Ana wind passes it. It is important to note that Riverside does not have the same slope as Los Angeles or Orange, since it has an increased CO concentration in vehicular emissions and the wind blowing into that particular sub-system has the highest CO concentration of all.

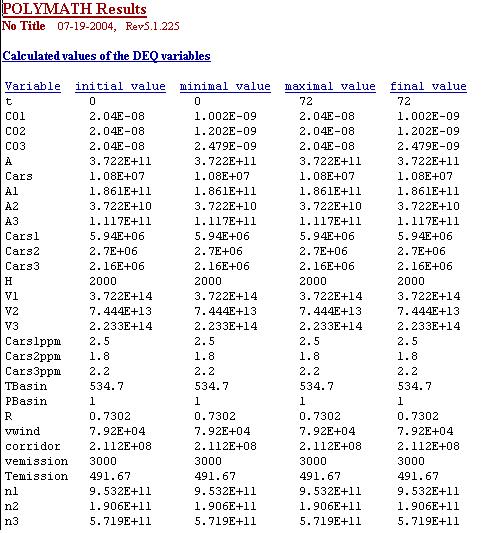
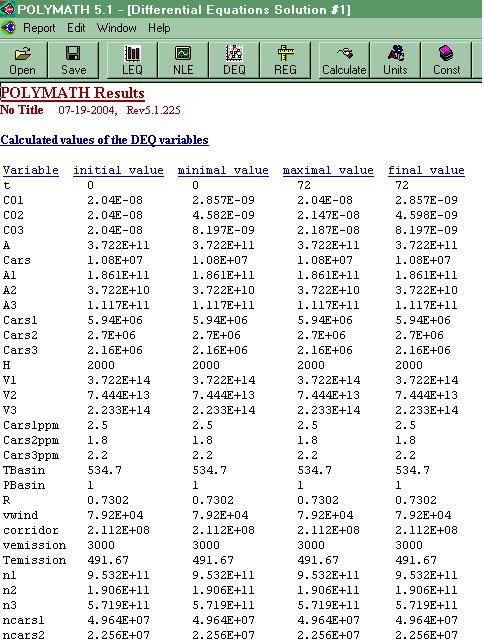
The actual results are illustrated in the picture below, obtained from Polymath:

If we applied the sine function to the vehicular emissions in the South Coast Air Basin, we would first need to modify the original Challenge equations as follows:

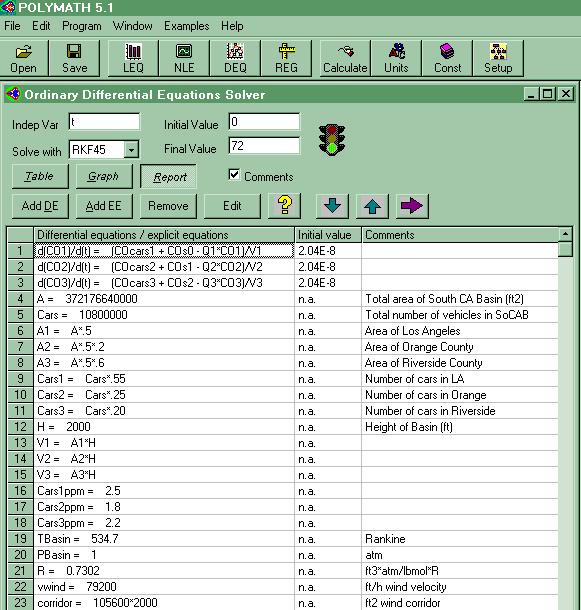
And afterwards come up with the following behavior:

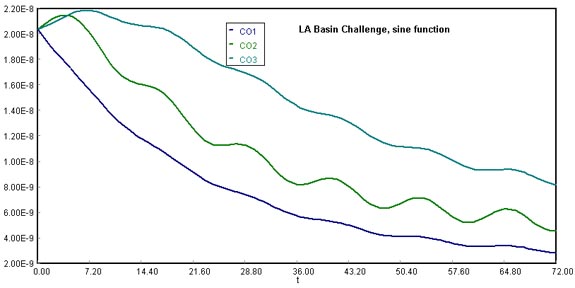
Notice that Orange County is the only basin that shows the accentuated effects of CO variation due to vehicular flow, and that Riverside will end up with a higher concentration of carbon monoxide in comparison with the other counties. During the first 7 hours of behavior, there is a hump effect in Orange and Riverside because of the sine function implemented in the system. Notice that this effect is also perceiveable in the original scenario, where there is no oscillation due to vehicular flow. The final results are included in this last image: