Check out the following YouTube Video: >Multiple Oscillating Reactions">

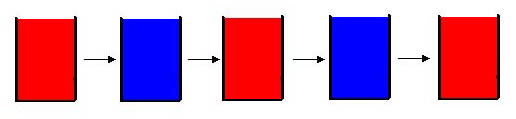
The Belousov-Zhabotinsky (BZ) reaction is a chemical oscillatory reaction, fluctuating in color. Named after B. P. Belousov (who discovered the reaction) and A. M. Zhabotinsky (who continued Belousovīs early work), the reaction originally consisted of a one-electron redox catalyst, an organic substrate that is easily brominated and oxidized, and a bromate ion in form of NaBrO3 or KBrO3 all dissolved in sulfuric or nitric acid. The typical catalyst that is used is ferroin. Ferroin, in its oxidized state, has a blue color, while in its reduced state ferroin is red. As the BZ reaction alternates between the oxidized state and reduced state, the solution changes its color.
In order to demonstrate the oscillations in the simplest manner possible, we will use the following idealized set of reactions, involving the dissociation of NaIO3 and the subsequent reactions of IO3. We will consider each one as elementary.
The main species important to the oscillation in this reaction are NaIO3, IO3-, I-, and I2.To make things easier in writing the mole balances and rate laws, we will say that: A = NaIO3, B = IO3-, C = I-, D = 1/2 I2. The series of reactions can then be written as:
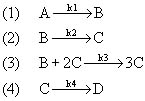
To model this series of reactions, we use our problem solving algortihm. Doing so, our first step is to write the mole balances for the reaction. The reaction is batch, and constant volume and we obtain:
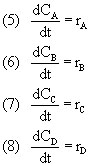
Next, we find the rate law for each reaction.
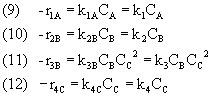
Our third step is stoichiometry...(Note that for every mole of B consumed in Reaction 3, one mole of C is produced. 3-2=1, and so r3C=-r3B)
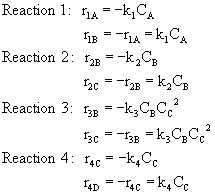
Finally, we find the net rates of reaction and combine...
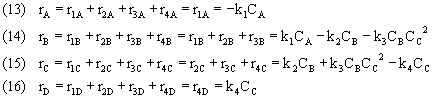
Our final batch mole balances look like this:
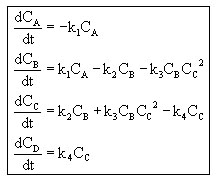
with k1=0.001 min-1, k2=0.01 min-1 , k3=2.5*109 dm6/mol2/min, and k4= 1 min-1
We can now put the final batch mole balances and the values for the rate constants into an ODE solver, such as Polymath. We will use the following initial concentrations: CAO=0.01 mol/dm3, CBO=2*10-5 mol/dm3 , CCO=1*10-5 mol/dm3, and CDO=0. The Polymath code will look like this:

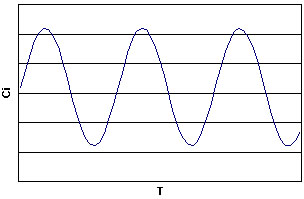
Graphing this, we get...
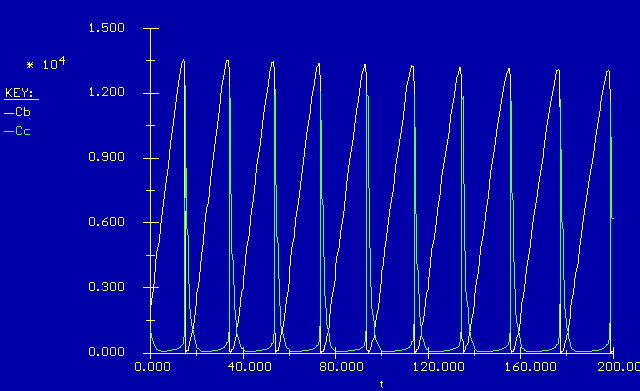
Now looking at the graph, we see the oscillations in the concentrations of B and C. Notice that the oscillations are periodic, and look like they can be modeled by sine and cosine functions. Also notice that the decline in the concentration of B, corresponding to the rise in the concentration of C appears to occur rather fast. Taking a closer look...
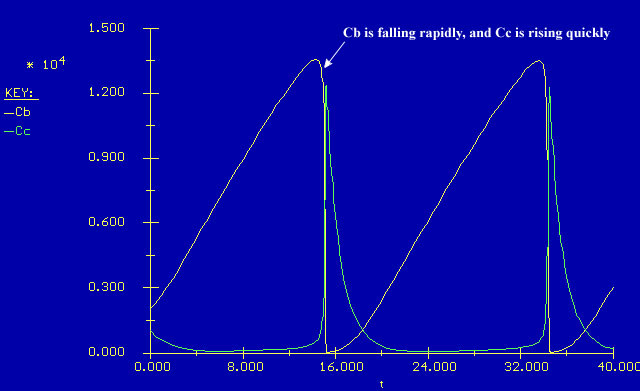
....we see this is true. Why is this?
Notes on Oscillating Reactions
Remember again that this series of reactions is merely a simplified model to help you understand how the BZ reaction scheme works. The actual BZ scheme involves over 40 seperate reactions, and is therefore quite difficult to model. However, this does provide a good basis for the BZ reactions and their application to multiple reactions in chemical reaction engineering. With all this in mind, try to answer the following questions concerning the reaction:
1) What factors influence the amplitude and frequency of the reaction?
2) It is known that the BZ oscillations eventually cease (in the original experiment by Belousov, they lasted about 50 minutes). Why do you think that is?
3) What causes these oscillations? (In other words: What makes this reaction different than others we have studied so far?)
4) Play around with the Polymath program above- what are the effects of changing the values of k1, k2, k3, and k4? Can you make the oscillations damped or unstable?
To see an actual video of a modified BZ reaction please click on the picture below. A short avi movie will show blue and purple oscillations.

(
Windows Media Player,
QuickTime Player,
Direct link
)
(Movie - 5.1MB)
NOTE: You will need the
QuickTime Plug-in
or
Windows Media Player
to view this movie.
Now, going back to the actual BZ reaction scheme itself, as mentioned earlier there are over 40 reactions to consider. Many of these reactions are minor, and so we are able to reduce the scheme to just 15 reactions, which are shown below.
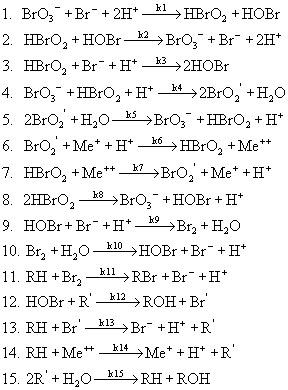
In the above scheme, BrO2', R', and Br' are free radical intermediates. RH is malonic acid and Me represents a metal ion. Notice that reactions #1 and 2, #4 and 5, #6 and 7, and #9 and 10 are essentially the same reaction, with one case being the reverse of the other. Because of this, in writing the rates of reaction we can reduce the number from 15 to 11. These 11 rates are shown below, with respect to a single mole of reactant.
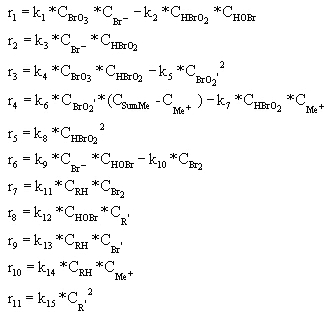
CBrO3 represents the stationary concentration of BrO3-, CRH represents the stationary concentration of RH, and CSumMe is the sum of the Me+ and Me++ concentrations. Putting the BZ scheme into Polymath with the appropriate rate constants, we get the following program.
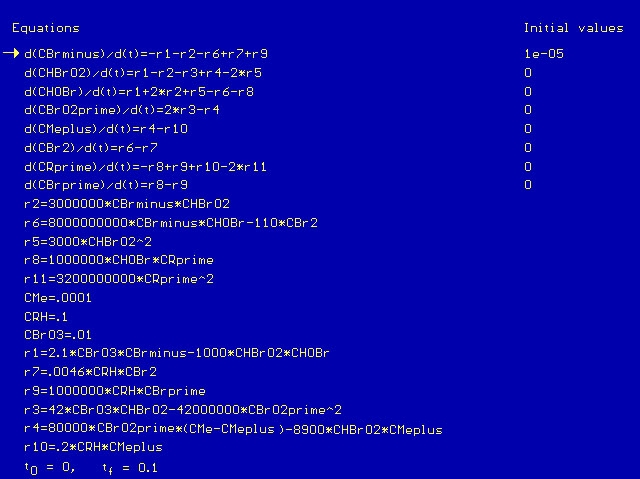
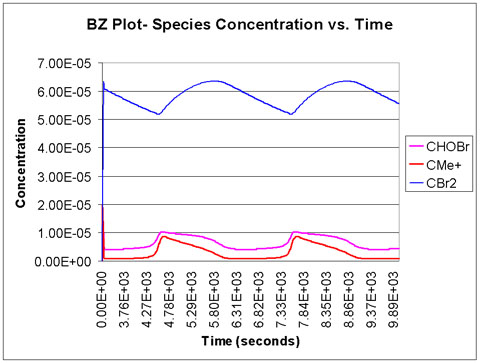
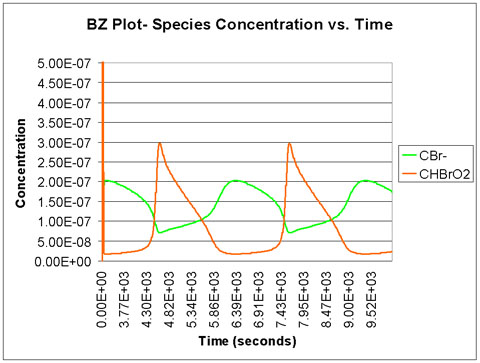
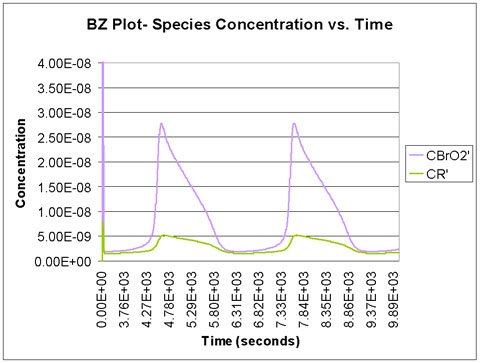
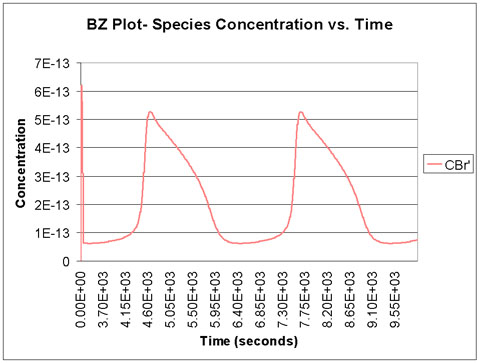
We run the program with a time scale of about 3 hours. The species concentrations as a function of time are shown below. We see that all eight major species do in fact oscillate with time.