

Trying a CSTR
Let's try a CSTR. The mole balances for CSTR give:cA-cA0 = (-k1cA + k2cB - k4cA2)t
cB-cB0 = (k1cA - k2cB - k3cB)t
The space time of the CSTR is given by t.
The equations describing the CSTR result in a set of algebraic equations that must be solved simultaneously for a given space time. We can now plot the different products for various space times.
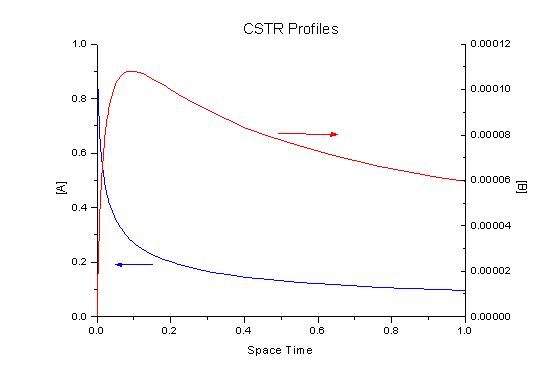
Again we can write the equations in vector notation:
cA-cA0 = (-k1cA + k2cB - k4cA2)t cB-cB0 = (k1cA - k2cB - k3cB)t [cA-cA0, cB-cB0] = [cA, cB] - [cA0, cB0] = [(-k1cA + k2cB - k4c A2), (k1cA - k2cB - k3cB)]t
Notice that the vector containing the kinetics is the same as that for a PFR.
We can more easily compare the productions of B versus the consumption of A for the PFR and CSTR by constructing a state-space plot. In the system we are considering, the state of the system is characterised by the concentrations of A and B. This is because we are not interested in the space time of the reactors but in the selectivity of B.
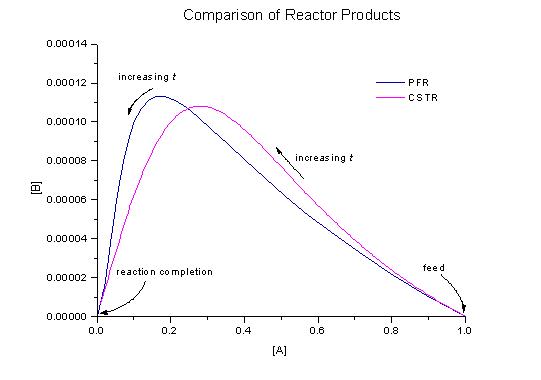
Lets do some comparisons of these two reactors. If we had a PFR of space time of t = 0.023s and a CSTR of space time t = 0.078s, which should we use? To work this out we use the graphs of the PFR profile and the CSTR products. A comparison is given in the table below:
| Reactor | Space Time | Effluent concentration of A | Effluent concentration of B |
| PFR | 0.023 s | 0.3 kmol/m3 | 0.97 x 10-4 kmol/m3 |
| CSTR | 0.078 s | 0.3 kmol/m3 | 1.08 x 10-4 kmol/m3 |
So for a conversion of A of 0.7 it is better to use a CSTR that a PFR. You should be able to easily see this by looking at the plots of cB versus cA for the PFR and CSTR.
What if we had a PFR of space time 0.057s and a CSTR of space time 0.38s, which should we use? This time we get the following:
| Reactor | Space Time | Effluent concentration of A | Effluent concentration of B |
| PFR | 0.057 s | 0.15 kmol/m3 | 1.11 x 10-4 kmol/m3 |
| CSTR | 0.38 s | 0.15 kmol/m3 | 0.85 x 10-4 kmol/m3 |
So for a conversion of A of 0.85 it is better to use a PFR that a CSTR. Again, you should be able to check this on the differnt plots.
Let's have a closer look at the plot state-space plot of cB versus cA. The reactor to choose based on the conversion of A is given by the table below:
| Conversion of A | X < 0.76 | X > 0.76 |
| Concentration of A | cA > 0.24 kmol/m3 | cA < 0.24 kmol/m3 |
| Best reactor | CSTR | PFR |
The most B is produced in a PFR with an effluent concentration of A 0.17 kmol/m3, that is at a conversion of A of 0.83. Thus, out of the PFR and the CSTR, the PFR results in the greatest production of B. Can we do any better that this?