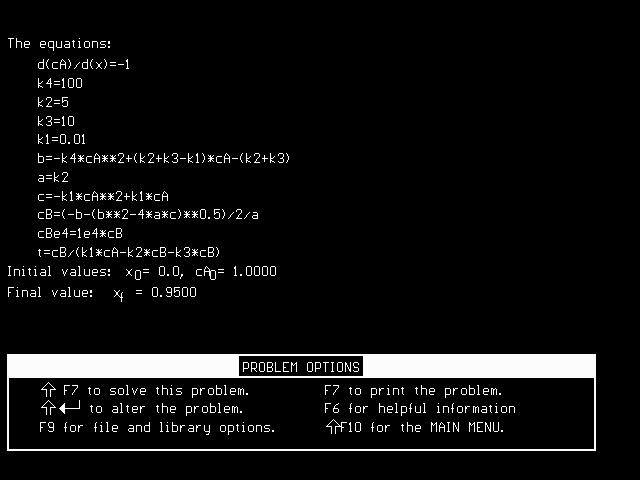
Solving the CSTR Equations in PolyMath

The equations describing the CSTR were shown to be:

c_A - c_A⁰ = (-k1cA+k2cB-k4cA^2)*t

c_B - c_B⁰ = t*S⁴_i=1 r_iB = (k1cA-k2cB-k3cB)*t

We need to solve these two equations simultaneously for a given t. We start by diving the two equations to eliminate t.

(c_A - c_A⁰) / (c_B - c_B⁰) = (-k1cA+k2cB-k4cA^2)/(k1cA-k2cB-k3cB)
(c_A - c_A⁰)*(k1cA-k2cB-k3cB) - (c_B - c_B⁰)*(-k1cA+k2cB-k4cA^2) = 0

We can multiply this out to obtain a quadratic in c_B. Substituting for no B in the feed, c_B⁰ = 0, we obtain the following quadratic equation:

a*c_B² + b*c_B + c = 0
a(c_A) = -k1*c_A² + k1*c_A*c_A⁰
b(c_A) = -k4*c_A² + (k2+k3-k1)*c_A - (k2+k3)*c_A⁰
c(c_A) = k2

c_B(c_A) = (-b(c_A) +/- (b(c_A)² - 4*a(c_A)*c(c_A))^0.5) / (2*a(c_A))

Finally, we can deterine the space time of the CSTR from:

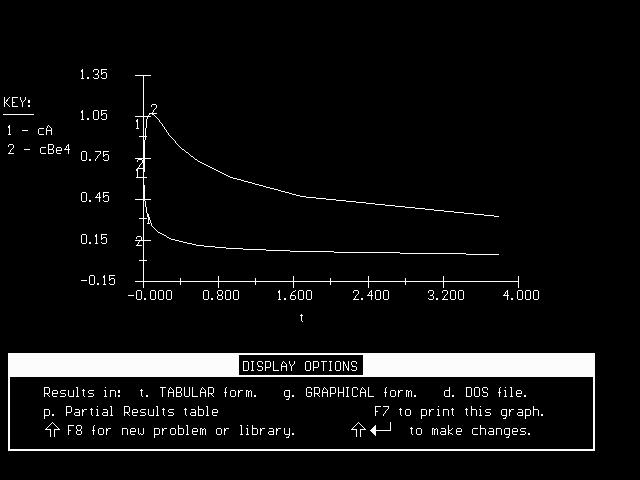
t = c_BA / (k1cA-k2cB-k3cB)

We can plot the solution in PolyMath using the following procedure:

CSTR Equations in PolyMath

CSTR Plot in PolyMath

Return