Chapter 1 Self Test

What You Have Learned?

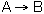
1. The rate law

(a.) is a differential equation    T     F
(b.) relates reaction rate and concentration of reacting species     T     F
(c.) is only valid in the U.S.    T     F
(d.) is a function of temperature;   T     F
2. The rate of formation of species A is per unit volume is

(a.) r_A    T     F
(b.) -r_A    T     F
(c.) the rate of generation of species A per unit volume    T     F
(d.) r'_A    T     F
(e.) none of the above    T     F
(f.) not used in Canada    T     F
3.
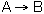
At a particular time t, the rate of formation of B in the reaction, r_B, is 10 mole/dm³*min. Which of the following are true?

The rate of disappearance of B is -10 moles/dm³*min.

The rate of formation of A is -10 mole/dm³*min.

The rate of disappearance of A is 10 moles/dm³*min.

r_A = -10 moles/dm³*min

-r_A = 10 moles/dm³*min

-r_B = -10 moles/dm³*min

Some of the above

All of the above

None of the above

A will disappear faster if a magician is present

Solution

Solutions

1 (a.) FALSE

F. The rate law is an algebraic equation relating the rate of reaction with the concentration of the reacting species. Example, for the elementary reaction
the rate law is:
Return to Problem 1

1 (b.) TRUE

-r_A = function (temperature and reacting species concentration), e.g.

IfDC_P = 0, then

otherwise, see p. 930 of text.

Return to Problem 1

1 (c.) FALSE It's also valid in Canada and the northern Provinces

Return to Problem 1

1 (d.) TRUE (Page 5 of Text)

Return to Problem 1

2 (a.) TRUE (Page 8 of Text)

r_A=moles of A formed, per unit time, per unit volume

[r_A]~[mol/dm³ s]

Return to Problem 2

2 (b.) FALSE (Pages 3 and 5 of Text)

-r_A is the rate of disappearance of A, [mol/dm³ s]

Return to Problem 2

2 (c.) TRUE

rate of formation=rate of generation

Return to Problem 2

2 (d.) FALSE (Page 6 of Text)

r'_A is the rate of disappearance of A per mass of catalyst, i.e. grams of catalyst [mol/kg cat s]

Return to Problem 2

2 (e.) FALSE (a & c are true)

Return to Problem 2

2 (f.) TRUE

The Toronto Maple Leafs Hockey Team has little use for rate of formation of species A.

Return to Problem 2

At a particular time t, the rate of formation of B in the reaction, r_B, is 10 mole/dm³*min. Which of the following are true?

The rate of disappearance of B is -10 moles/dm³*min.

The rate of formation of A is -10 mole/dm³*min.

The rate of disappearance of A is 10 moles/dm³*min.

r_A = -10 moles/dm³*min

-r_A = 10 moles/dm³*min

-r_B = -10 moles/dm³*min

Some of the above

All of the above

None of the above

A will disappear faster if a magician is present

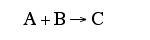
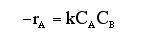
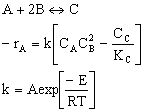
Solution

h. (all are true)

Explanation

Consider a constant volume (V = V₀) batch system

Equivalently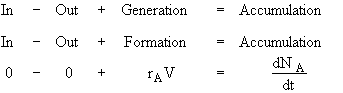

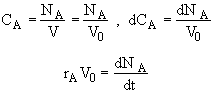
At t = 0 then. A moment later at t = 0.01 sec then. If were to be positive, the concentration of A would increase with time. However, A is being consumed so the concentration of A is decreasing with time. For small times we use a different formula to find.

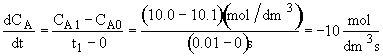
The rate of formation of A is

�B� is being formed

Back to Chapter 1