Consider a cluster consisting of n_g molecules with n_s molecules attached to the surface.

The Gibbs free energy, G(kJ) of a cluster of n_g molecules plus n_s surface molecules is the sum of the Gibbs free energy of a cluster (G_c) (kJ/molecule) plus the Gibbs free energy of the surface moles (G_s) (kJ/molecule)

                                                                                                                     (1)

Adding and subtracting n_sG_c to the r.h.s. of Equation (1)

                                                                                               (2)

Neglecting the number of monomers on the surface wrt to the number monomers in the cluster (n_s << n_c) we have

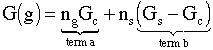                                                                                                        (3)

We now will evaluate each term, starting with (term b). Term b is the difference in free energy between the surface molecules and the bulk “solid” cluster and is equal to the product of the surface tension and the surface area of the cluster [see Everett, D. H. “Basic Principles of Colloid Science,” Royal. Soc. Chem.. 1989 p57, ISBN 0-85186-443-0].

            The free energy of the cluster can now be written

                                                                                 (4)

The molecular Gibbs free energy of the molecules inside the cluster, G_c, is just the molecular chemical potential m_g. Consequently the Gibbs free energy of the surface molecules plus the cluster molecules are

                                                                                                             (5)

The change in the Gibbs free energy is going from n_g individual molecules in bulk solution at a mole fraction X to a cluster of size g with chemical potential m_i is

                                                                                                                          (6)

Substituting for G(g)

                                                                                                       (7)

where m_i is the chemical potential of the monomer molecule. For dilute solutions, the chemical potential of the monomer in the dispersed phase is

                                                                                                                           (8)

where X is the mole fraction of monomer in the gas. The chemical potential of the bulk solid corresponds to saturation corresponds to saturated conditions, X_sat

                                                                                                                    (9)

Combining Equations (7), (8), and (9) and setting n_g º n.

                                                                                                     (10)

but S = X/X_sat

                                                                                                          (11)

where again n is the number of monomers in the cluster

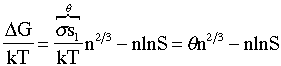
                                                                                                                       (12)

In terms of g-mers (n º g)

Back to Nucleation Kinetics