

For this module there are a couple of topics that need to be reviewed or
dicussed:
1) Semibatch reactor equations
2) Modifications due to reactive distillation


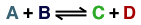
Shown above is a representation of a typical semibatch reactor. B is
fed to A, which is already in the reactor, and there are no outputs
(evporation included). To model a semibatch reactor, start with a mole
balance on each species :

Starting with species A :

|
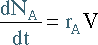
|
C and D are similar :
 |
 |
||||
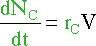 |
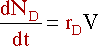 |
||||
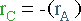 |
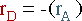 |
||||
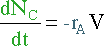 |
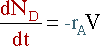 |
Species B is fed to the reactor
making its mole balance equation slightly different :
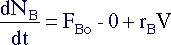 |
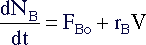 |
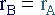 |
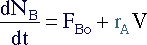 |
We now have all the equations needed to describe the changes in concentration of the different species in the reactor over time. However, since there is a feed stream, the volume in the reactor will change. So, we need to develop an equation describing how the volume in the reactor changes with time.
Starting with a mass balance and remebering that mass can neither be
created nor destroyed :


The mass terms in the equation can be replaced by :
 |
 |
 |
||||
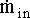 |
 |
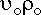 |
||||
 |
 |
 |
giving :

Assuming that the system is at constant density leads to :

That is the last equation needed to model the semibatch reactor.


| Mole Balance | Mass Balance | |||
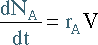 |
 |
|||
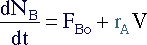 |
||||
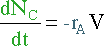 |
Rate Law | |||
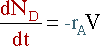 |
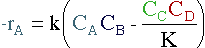 |
|||
Now we can move on and talk about reactive distillation.
|
|