The following liquid phase reaction follows an elementary rate law
![]()
The reaction is to be carried out in a PFR.
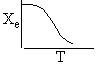
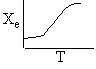
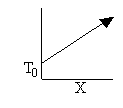
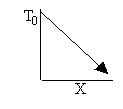
a) Write the CRE algorithm and then sketch the temperature as a function of conversion for an adiabatic endothermic reaction and an adiabatic exothermic reaction.
b) Write the adiabatic energy balance.
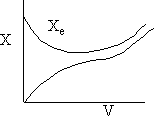
c) Use a sketch to show how to find the adiabatic equilibrium conversion and temperature for both an exothermic reaction and an endothermic reaction.
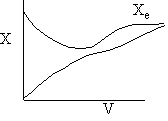
d) Sketch the adiabatic equilibrium conversion, the conversion and temperature for both an exothermic reaction and an endothermic reaction to show how they vary along the length of the reactor.
e) Write the energy balance for the case when a coolant is present
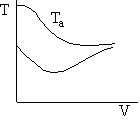
f) Sketch the temperature, equilibrium and conversion, add conversion profiles for both exothermic and endothermic reactions when the coolant temperature remains constant.
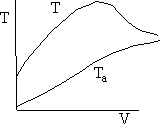
g) Sketch the temperature, equilibrium and conversion, add conversion profiles for both exothermic and endothermic reactions when the coolant temperature varies along the length or the reactor.
Solution
a) PFR Algorithm
Mole Balance ![]() Þ
Þ 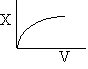
Rate Law
![]()
Stoichiometry ![]()
![]()
Combine 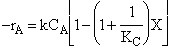 Þ
Þ 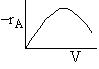
@ Equil -rAº 0
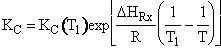
Exothermic Endothermic
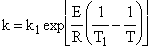 Þ
Þ 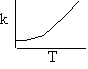
Adiabatic Energy Balance
Exothermic Endothermic
b)
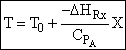
c)
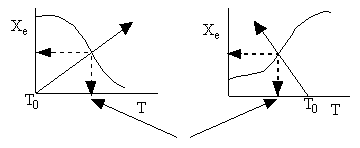
Adiabatic Equilibrium
Temperature and Conversion
d) Adiabatic Temperature and Conversion Profiles
Exothermic Endothermic
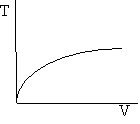
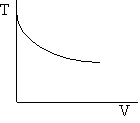
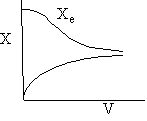
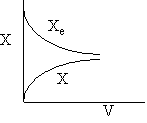
e) Energy Balance with Heat Exchange
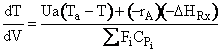
f) Constant Coolant Temperature Ta
Exothermic Endothermic


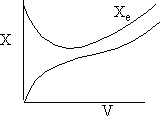
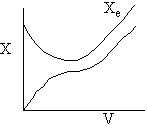
g) Variable Coolant Temperature Ta
Exothermic Endothermic