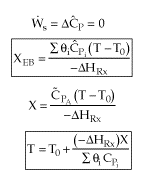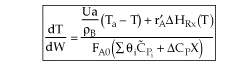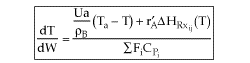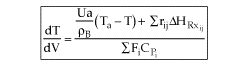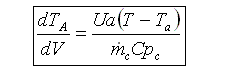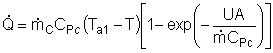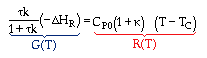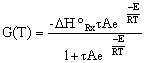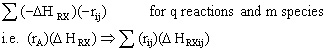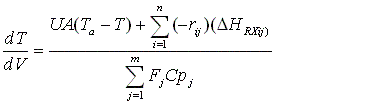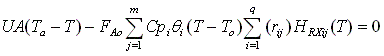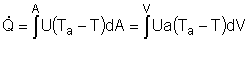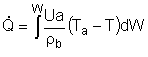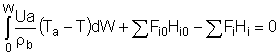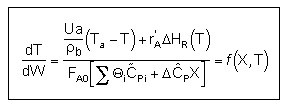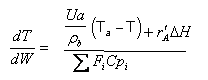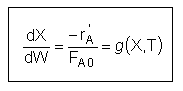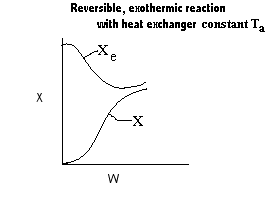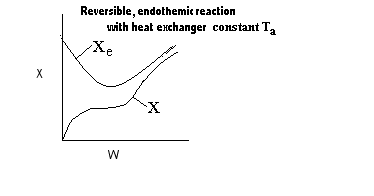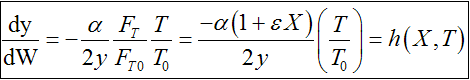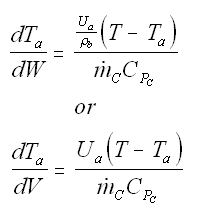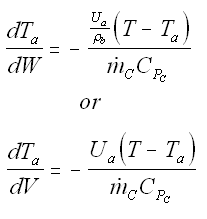12. Steady-State Non-Isothermal Reactor Design : The Steady State Energy Balance and Adiabatic PFR Applications
*
Topics
- Overview of User Friendly Energy Balance Equations
- Evaluating the Heat Exchanger Term
- Multiple Steady States
- Multiple Reactions with Heat Effects
- Applications of the PFR/PBR User
Friendly Energy Balance Equations
|
User Friendly
Energy Balance Equations |
top |
The user friendly forms of the energy balance we will focus on are outlined
in the following table.
User friendly equations relating X and T, and Fi and T
1. Adiabatic CSTR, PFR, Batch, PBR achieve this:
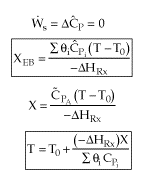
|
(1.A)
(1.B) |
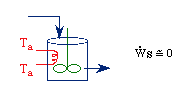
2. CSTR with heat exchanger, UA(Ta-T) and large coolant flow rate.
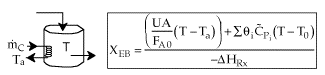
|
(2) |
3 . PFR/PBR with heat exchange
3A. In terms of conversion, X
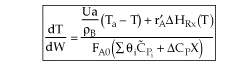
|
(3.A) |
3B. In terms of molar flow rates, Fi
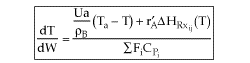
|
(3.B) |
4. For Multiple Reactions
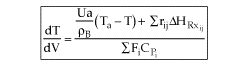
|
(4) |
5. Coolant Balance
Co-Current Flow
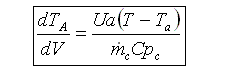 |
(5) |
|
These equations are derived in the text. These are the equations that we
will use to solve reaction engineering problems with heat effects. |
|
Evaluating the Heat Exchanger Term
|
top
|

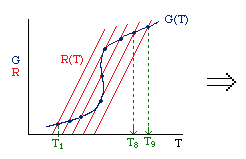
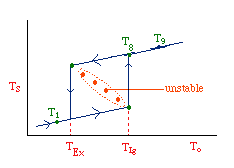
CSTR with Heat Effects

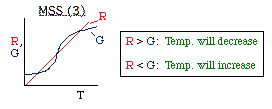
Finding when R(T) = G(T)

Finding MSS for an Endothermic Reaction
Now we need to find X. We do this by combining the mole balance, rate law, Arrhenius
Equation, and stoichiometry.
For the first-order, irreversible reaction A -->
B, we have: 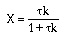
|
where |
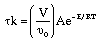 |
At steady state: |
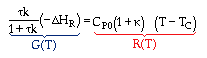 |
Substituting for k... |
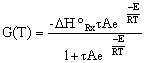
|
 |
 |
|

Generating G and R verse T: Single Reaction
| Multiple Reactions with Heat Effects |
top |
To account for heat effects in multiple reactions, we simply replace the term (-delta HRX)
(-rA) in equations (12-35) PFR/PBR and (12-40) CSTR by:
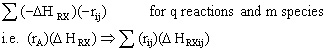
PFR/PBR
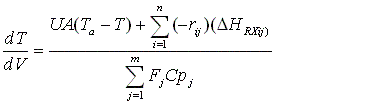
CSTR
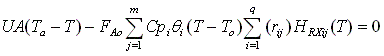
These equations are coupled with the mole balances and rate law equations discussed in
Chapter 6.
 Textbook Example
Textbook Example
(Alternative Solution)
Complex Reactions
Example: Consider the following gas phase reactions
|
Combined Mole Balance, Rate Law, Stoichiometry, and Energy Balance:
|

We now substitute the various parameter values (e.g. delta HRX, E, U) into
equations (1)-(13) and solve simultaneously using Polymath.

Multiple Reactions in a PFR with Variable Coolant Temperature
|
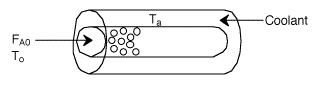
Applications of the PFR/PBR User Friendly Energy Balance Equations
|
top
|
NOTE: The PFR and PBR formulas are very similar.
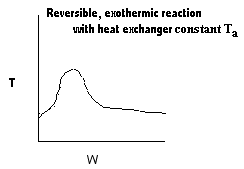 |
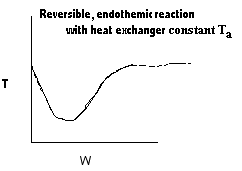 |
| |
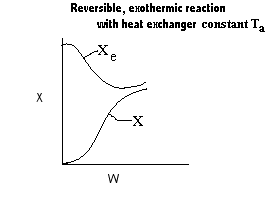 |
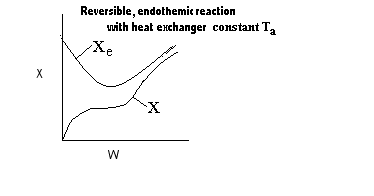 |
If we include pressure drop: |
C. 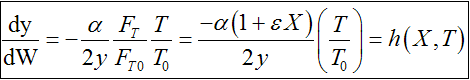
|
Note: the pressure drop will be greater for exothermic adiabatic reactions than it will be for isothermal reactions |
 |
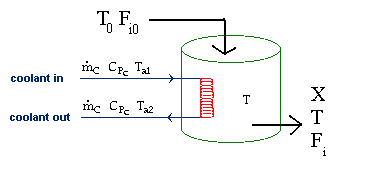
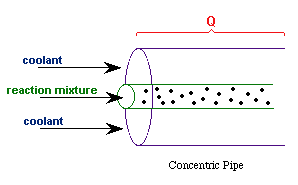
Balance on Heat Exchanger Coolant
Solve simultaneously using an ODE solver (Polymath/MatLab). If Ta
is not constant, then we must add an additional energy balance on
the coolant fluid: |
| Co-Current Flow |
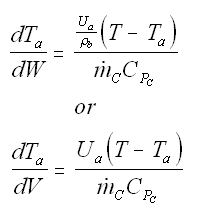 |
|
| Counter-Current Flow |
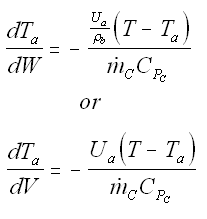
with Ta = Tao at W = 0 |
For an exothermic reaction: with counter current heat exchange
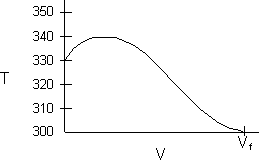
A Trial and Error procedure for counter current flow problems is required to find exit conversion and temperature.
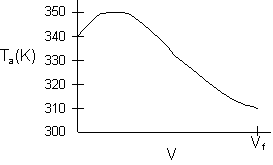
- Consider an exothermic reaction where the coolant stream enters at the end of the reactor at a temperature Ta0, say 300 K.
- Assume a coolant temperature at the entrance (X = 0, V = 0) to the reactor Ta2 =340 K.
- Calculate X, T, and Ta as a function of V. We can see that our guess of 340 K for Ta2 at the feed entrance (X = 0) gives a coolant temperature of 310 K, which does not match the actual entering coolant temperature of 300 K.
- Now guess a coolant temperature at V = 0 and X = 0 of 330 K. We see that the exit coolant temperature of Ta2 = 330 K will give a coolant temperature at V = V1 of 300 K.

A ↔ B Liquid Phase Adiabatic

A ↔ B Liquid Phase Constant T
a

A ↔ B Liquid Phase Variable T
a, Co-Current

A ↔ B Liquid Phase Variable T
a, Counter Current

Sketch the Ambient Temperature as a function of V.

Elementary Liquid Phase Reaction

Exothermic, Reversible Reaction

Adiabatic Reaction in a PBR.

PBR with heat exchange.

PBR with heat exchange and variable coolant flow rate.

Nonisothermal Reactions.

LEP 12-T12-3: Variable Coolant Temperature.

Objective Assessment of Chapter 12
*
All chapter references are for the 1st Edition of the text Essentials of Chemical Reaction Engineering
.
top