EQUATIONS
Energy balance
The equation below formulates the general energy balance that takes into consideration radial variations in a tubular reactor. In Chapter 8, section 8.9 you can see the derivation of the energy balance.
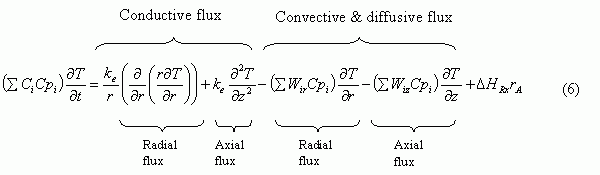
Where Cpi is the heat capacity of species i,
T the temperature,
ke the thermal conductivity of the reaction mixture,
Wir
and Wiz are the radial and axial fluxes of species i respectively,
![]()
![]() (see Chapter 11 of CRE)
(see Chapter 11 of CRE)
![]() the heat of reaction,
the heat of reaction,
and -rA the reaction rate based on the limiting species A. For example, the reaction rate for an elementary first-order reaction can be expressed as: -rA = kCA
Similar to the Eqn (1) for the mass balance, the term on the left hand side represents accumulation of energy. The first and the second term on the right hand side represents the conductive fluxes in the radial and axial directions respectively. The two following terms represents heat flux generated by a flux in mass. This flux consists as always of two parts; Flux by diffusion and convection. The last term represents the heat production through the heat of reaction. So, a difference in energy flux over a volume element is either due to accumulation of heat or the production or consumption of it.
Assumptions
In the same way that the expression for the mass balance can be simplified for steady-state conditions, so can the energy expression:
![]() (7)
(7)
The convective flux in the radial direction is smaller than the diffusive
flux and can therefore be neglected, i.e.
![]() (8)
(8)
Furthermore, we assume that Uz is constant throughout the length of the reactor and equal to the inlet velocity and that the convective flux is greater in the axial direction than the diffusive flux. Therefore the axial flux will only consist of the convective term.
![]() (9)
(9)
The convective energy flux in the radial direction can be neglected with respect to the conductive flux, i.e.
![]()
![]()
Then Eqn (9) becomes
![]() (10)
(10)
Finally, we expand the radial conduction term and change the axial convection term slightly. CiCpi is equivalent to ρiCpi if Cpi is mass based instead of molar based. Assuming that ρCp is constant, the energy balance becomes:
![]() (11)
(11)
Eqn (5) and (11) represents the simplified general forms of Eqn (1) and (6) that has been used by COMSOL Multiphysics to solve the problem stated above.