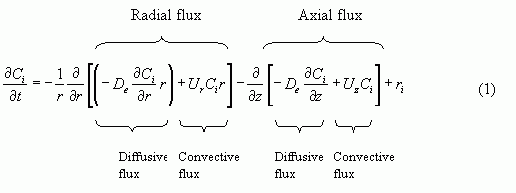
The equation below formulates the general mass balance that takes into consideration radial variations in a tubular reactor. In Chapter 8, section 8.9 you can see the derivation of the mole balance.
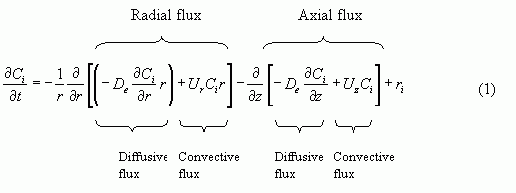
Where Ci is the concentration of species i, (mole/m3)
De the effective diffusivity, (m2/s)
Ur and Uz the superficial velocity in the radial and axial directions respectively, (m/s)
and ri the reaction rate of species i (ri = v i*(-rA)), (mole/m3/s)
In Eqn (1), the term on the left hand side represents accumulation. The first two terms on the right hand side represents the difference in flux over a volume element. The total flux consists of two parts; Flux by diffusion and convection both in a radial direction and axially.
If the flux of one species out of the specific volume element is less than the flux going in to the same element, that implies that this species is accumulating or disappearing through reaction. Therefore the sum of the accumulation and the net flux equals the reaction rate.
Because the reaction is studied under steady-state conditions, Eqn (1) can be simplified by neglecting the time dependent accumulation term.
![]() (2)
(2)
The convective flux in the radial direction is smaller than the diffusive flux and can therefore be neglected, i.e. Ur is approximately 0. Therefore the radial flux will only consist of the diffusive term.
![]() (3)
(3)
Furthermore, we assume that Uz is constant and equal to the inlet velocity throughout the reactor.
![]() (4)
(4)
Expanding the derivative of the radial diffusivity yields the final form of the general mass balance being used in this exercise:
![]() (5)
(5)