


Next: Feladat: hanghullám TVD-MUSCL módszerrel
Up: Gáz és plazma dinamika
Previous: Feladat: hanghullám MacCormack módszerrel
Tartalomjegyzék
Az elõzõ fejezetben feladatának megoldásából kiderül, hogy a stabil
és másodrendû MacCormack módszer meglehetõsen pontatlan eredményt
ad a hanghullámok terjedését modellezõ szimulációban. Ezen nyilván
segítene, ha addig növelnénk a rácsfelbontást, amíg a megoldás
pontossága elfogadhatóvá nem válik. Ez egy egyszerû egy dimenziós
problémára könnyen megtehetõ, de több dimenziós szimulációknál
a rendelkezésre álló számítógépidõ és memória behatárolja
a használható rácsfelbontást.
Az (15) algoritmussal definiált elsõrendû upwind
módszert próbáljuk meg úgy másodrendûvé fejleszteni, hogy
megõrizze azt a jó tulajdonságát, hogy nem generál oszcillációkat.
Ezt a tulajdonságot pontosabban is meg lehet fogalmazni: az upwind módszer
nem növeli a megoldás teljes variációját, amit diszkretizált
formában a
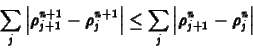 |
(41) |
egyenlõtlenség fejez ki. Bebizonyítható, hogy az upwind módszer
által adott megoldás skalár egyenletre mindig teljesíti a
(41) feltételt, azaz az upwind algoritmus egy
teljes variációt csökkentõ módszer - angolul ,,total variation
diminishing'' (TVD). A TVD módszerek nyilvánvalóan stabilak és
oszcilláció mentesek, hiszen egy instabilitás vagy oszcilláció
mindig a
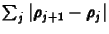 teljes variáció növekedésével
jár.
teljes variáció növekedésével
jár.
Próbáljunk meg egy másodrendû TVD módszert kifejleszteni. Elõször
írjuk át a (15) algoritmust egy kompakt, feltételes
elágazástól mentes formába:
![\begin{displaymath}
\rho^{n+1}_j=\rho^n_j-v\frac{\Delta t}{2\Delta x}
\left[v ...
...)
-\vert v\vert(\rho^n_{j+1}-2\rho^n_j+\rho^n_{j-1})
\right]
\end{displaymath}](img149.gif) |
(42) |
Könnyen látható, hogy (42) és (15) ekvivalensek.
Tovább alakíthatjuk a formulát, ha a második tagot két diffuzív
fluxus különbségeként írjuk fel:
![\begin{displaymath}
\rho^{n+1}_j=\rho^n_j-v\frac{\Delta t}{2\Delta x}
\left[v ...
...j-1})\right]
+{1\over2}\left(\Phi_{j+1/2}-\Phi_{j-1/2}\right)
\end{displaymath}](img150.gif) |
(43) |
ahol a 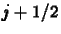 index az
index az
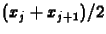 koordinátát jelöli, és
a diffúzív fluxus
koordinátát jelöli, és
a diffúzív fluxus
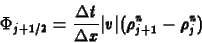 |
(44) |
A másodrendû módszer ezt a diffúzív fluxust csökkenti le
anélkül, hogy a TVD tulajdonság megszûnne. Definiáljuk a
értékeket, melyek 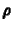 értékét kétféle módon becsülik
meg az
értékét kétféle módon becsülik
meg az 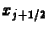 pontban:
pontban: 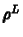 a bal oldali
a bal oldali
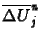 ,
míg
,
míg 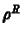 a jobb oldali
a jobb oldali
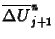 meredekséget használja fel. Ezek után a diffúzív fluxust
újradefiniálhatjuk:
meredekséget használja fel. Ezek után a diffúzív fluxust
újradefiniálhatjuk:
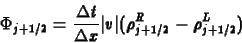 |
(46) |
Az így definiált 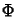 és a (43) algoritmus egy térben
másodrendû TVD módszert definiálnak a kontinuitási egyenletre. Ez
többféle módon is idõben másodrendûvé tehetõ valamint
általánosítható egyenletrendszrekre. Ezeknek a módszereknek
a részletes tárgyalásától itt el kell tekintenünk, csupán
annyit említünk meg, hogy a feladatokban az egyik ilyen általánosítást
fogjuk használni, mégpedig az úgynevezett TVD-MUSCL módszert,
mely nevét az angol ,,Monotonic Upstream Scheme for Conservation Laws'',
(monoton folyásirányú módszer megmaradási törvényekhez)
rövidítésébõl nyerte.
és a (43) algoritmus egy térben
másodrendû TVD módszert definiálnak a kontinuitási egyenletre. Ez
többféle módon is idõben másodrendûvé tehetõ valamint
általánosítható egyenletrendszrekre. Ezeknek a módszereknek
a részletes tárgyalásától itt el kell tekintenünk, csupán
annyit említünk meg, hogy a feladatokban az egyik ilyen általánosítást
fogjuk használni, mégpedig az úgynevezett TVD-MUSCL módszert,
mely nevét az angol ,,Monotonic Upstream Scheme for Conservation Laws'',
(monoton folyásirányú módszer megmaradási törvényekhez)
rövidítésébõl nyerte.
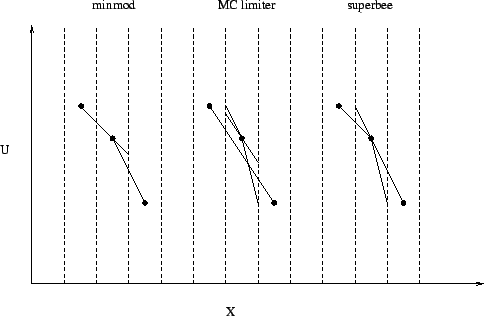
Ábra 3.:
Háromféle meredekség limiter. A vékony vonalak
a felhasznált, a vastag vonal a limitált meredekségeket
mutatja.
 |
A teljes variáció csökkentését
a meredekségek megfelelõ definíciója teszi lehetõvé.
A legegyszerûbb az úgynevezett minmod limitált meredekség:
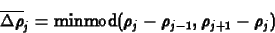 |
(47) |
ahol a
 függvény megegyezõ elõjelû argumentumokból
a legkisebb abszolútértékût adja vissza, ha viszont az argumentumok
között van két ellentétes elõjelû, akkor 0-t ad vissza.
Másképpen fogalmazva, a minmod limitált meredekség azonos elõjelek
esetén a bal és jobb oldali meredekségek közül a kevésbé meredeket
adja vissza, ellentétes elõjelnél pedig nullát.
függvény megegyezõ elõjelû argumentumokból
a legkisebb abszolútértékût adja vissza, ha viszont az argumentumok
között van két ellentétes elõjelû, akkor 0-t ad vissza.
Másképpen fogalmazva, a minmod limitált meredekség azonos elõjelek
esetén a bal és jobb oldali meredekségek közül a kevésbé meredeket
adja vissza, ellentétes elõjelnél pedig nullát.
Gyakran jóval pontosabb eredményt ad a monoton centrális (MC) limiter
használata:
![\begin{displaymath}
\overline {\Delta\rho}_j = \mathrm{minmod}\left[
2(\rho_j-...
...j-1}),2(\rho_{j+1}-\rho_j),
(\rho_{j+1}-\rho_{j-1})/2 \right]
\end{displaymath}](img168.gif) |
(48) |
ahol az utolsó argumentum a centrális meredekség, melyet a bal és
jobb oldali meredekségek kétszeresével limitálunk.
Az úgynevezett szuperbee limiter, melynek definíciójától itt
eltekintünk, még ennél is kevésbé köti
meg a meredekség értékét, azonban ez a gyakorlatban már
nem kívánatos meredekség élesedést okozhat. A három limiter
hatását a 3. ábra szemlélteti.
Alfejezetek



Next: Feladat: hanghullám TVD-MUSCL módszerrel
Up: Gáz és plazma dinamika
Previous: Feladat: hanghullám MacCormack módszerrel
Tartalomjegyzék
Gabor Toth
2000-09-04
