Joseph's home page

Current Research

My research interests include internal gravity waves, the dynamics of turbulent plumes and jets, turbulent fountains, and geophysical flows. I also enjoy using mathematical modeling and laboratory experimentation to understand buoyancy driven flows.

[1] Parameteric Subharmonic Instability in a global model (Ansong et. al, 2018)
On-going research is trying to understand the dynamic processes befalling internal tides before they finally dissipate. One such process is called Parameteric Subharmonic Instability (PSI), whereby a primary wave (the internal tide in this case) may lose energy to daughter waves with smaller vertical scales and with nearly half the frequency of the primary wave (McComas and Bretherton 1977). We examine whether PSI occurs in a high-resolution global model, forced by both atmospheric analyses fields and tides, and whether PSI accounts for a significant fraction of the tidal baroclinic energy loss.
	[Top] Predicted semidiurnal tidal signal of North-South baroclinic velocity close to location MP3 around Hawaii (longitude = 196.5 degrees East). [Middle] Same as top panel but after bandpassing around the subharmonic frequency band (half tidal frequency) for near-inertial waves. Observe high vertical wavenumber structures in the upper ocean around the critical latitude (white vertical line). [Bottom-left] A vertical profile through the M2 critical latitude (28.8 degrees North) from the middle panel, showing the vertical scale of the near-inertial waves. [Bottom-right] A horizontal slice from the bottom-left panel through 1000m depth, showing the horizontal scale of the subharmonic signals in the critical latitude band (25-30 degrees North).

[2] Variability of semidiurnal internal tides
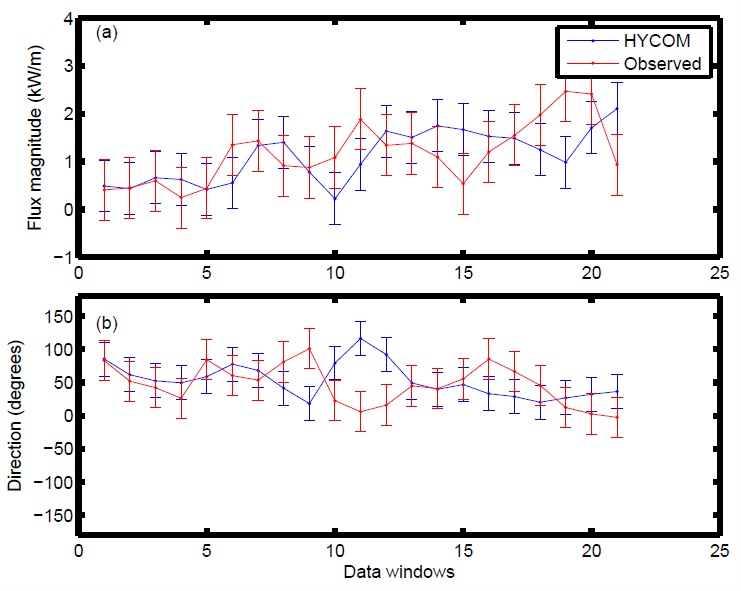
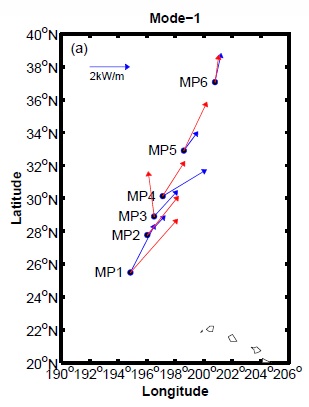
The root-mean-square (RMS) variability of the semidiurnal internal tide energy flux is large in both a global model, HYCOM, and moored observations. The normalized RMS variability (the RMS variability divided by the mean) is of order 23% or more in both the model and observations. The model fluxes agree more closely with the high-resolution observed (IWAP) fluxes than with those derived from historical moorings [see Ansong et al. (2017)].
Example time series of 1/25-degree HYCOM semidiurnal mode-1 baroclinic energy flux (a) magnitude and (b) direction; location: latitude=35.55 North, longitude= 142.66 East. The fluxes are divided into 50% overlapping 30-day windows. The vertical bars are envelopes of the magnitude-only [in (a)] and direction-only [in (b)] variabilities computed over all locations [Ansong et al 2017]	Map of depth-integrated semidiurnal mode-1 energy fluxes computed from 1/25 degree HYCOM (red arrows) and observations (blue arrows) from the IWAP experiment [Zhao et al., 2010]. Arrow lengths are logarithmic and reference arrows are shown at the upper left corner of each plot [Ansong et al 2017]

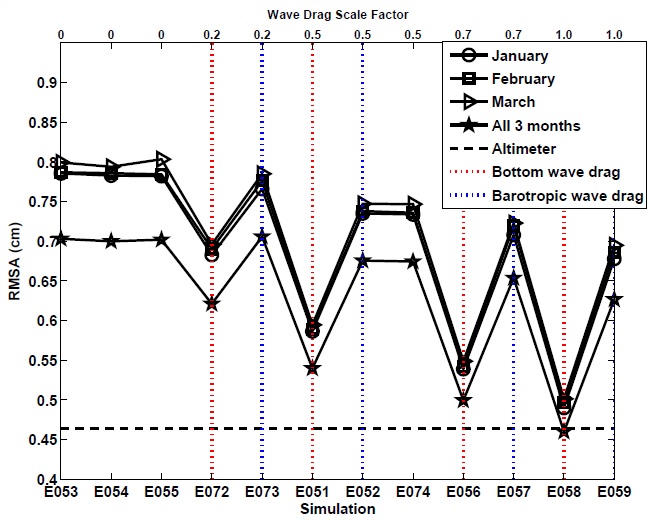
[3] Importance of parameterized wave drag in global ocean models
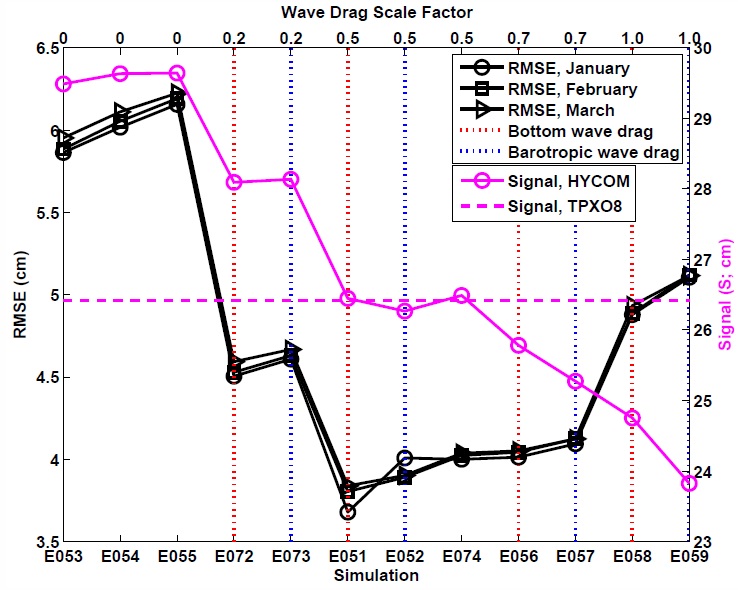
Without a parameterized internal wave drag in high resolution global ocean models, both the barotropic and baroclinic tides become too energetic, compared to TPXO and along-track altimeter data, and travel too far from their generation regions [see Ansong et al (2015)].
The root-mean-square error (RMSE; black curves) of HYCOM surface tidal elevations measured against TPXO8. The mean Signal, S, in HYCOM and TPXO8 are depicted in the magenta curves (right axis). The scale factor of the wave drag for each simulation is shown on the top axis and the bottom and barotropic drag simulations are denoted by red and blue vertical dotted lines respectively. [Ansong et al. 2015]	Globally-averaged root-mean-square amplitude, RMSA, of HYCOM baroclinic tidal elevations from all simulations versus the along-track altimeter value. The scale factor of the wave drag for each simulation is shown on the top axis and the bottom and barotropic drag simulations are denoted by red and blue vertical dotted lines respectively.[Ansong et al 2015]

Some previous research: laboratory tank experiments

[4] Internal gravity waves generated by convective plumes
	Movie: Internal gravity waves are generated when a turbulent plume, moving through a uniform ambient fluid (upper gray part of tank), impinges and penetrates a uniformly stratified layer of fluid. The waves radiate from the density interface as conical beams and finally reflect off the tank walls [J.K. Ansong and B.R. Sutherland, JFM, 2010].

[5] Turbulent Fountains in a two-layer fluid
	JFM cover figure: A laboratory tank experiment of a turbulent fountain penetrating the interface between two density layers, and reversing to spread along the neutral density level [J.K. Ansong, P. Kyba and B.R. Sutherland, JFM, 2010].