HOME
| RESEARCH
| PUBLICATIONS
|
ABOUT ME |
CONTACT | WHAT'S NEW? | CASSANDRA! |
فارسی | CHANNEL | OUTREACH | TEACHING | CV
Effects of earthuake radiation pattern and depth on seismic signals:
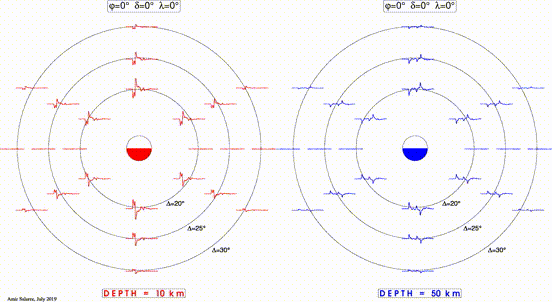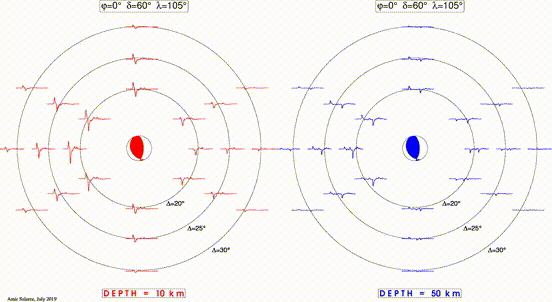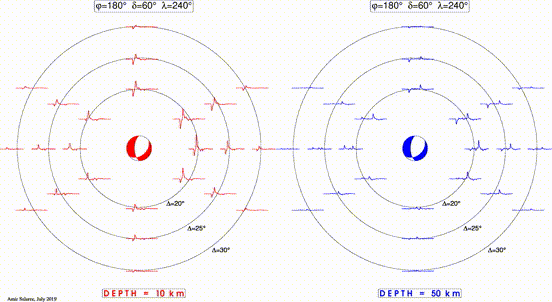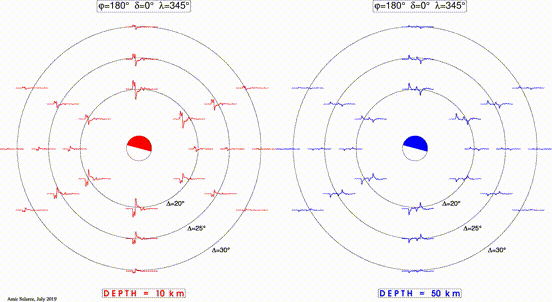
This animated (gif) cartoon shows the effects of focal mechanism & depth of earthquakes on recorded seismic signals.
Shoaling of long waves (e.g. tsunamis):
Simply put, shoaling happens because the gravity waves slow down as they approach the coastline on the coastal slopes. The speed gradient at the front (slower) and back (faster) ends of a wave results in a shortening of the wave. Conservation of mass and momentum then dictate that the shortening is compensated by an increase in wave height.
A simple analogy of the shoaling process is traffic pile-up, as I have tried to show in the cartoon below:

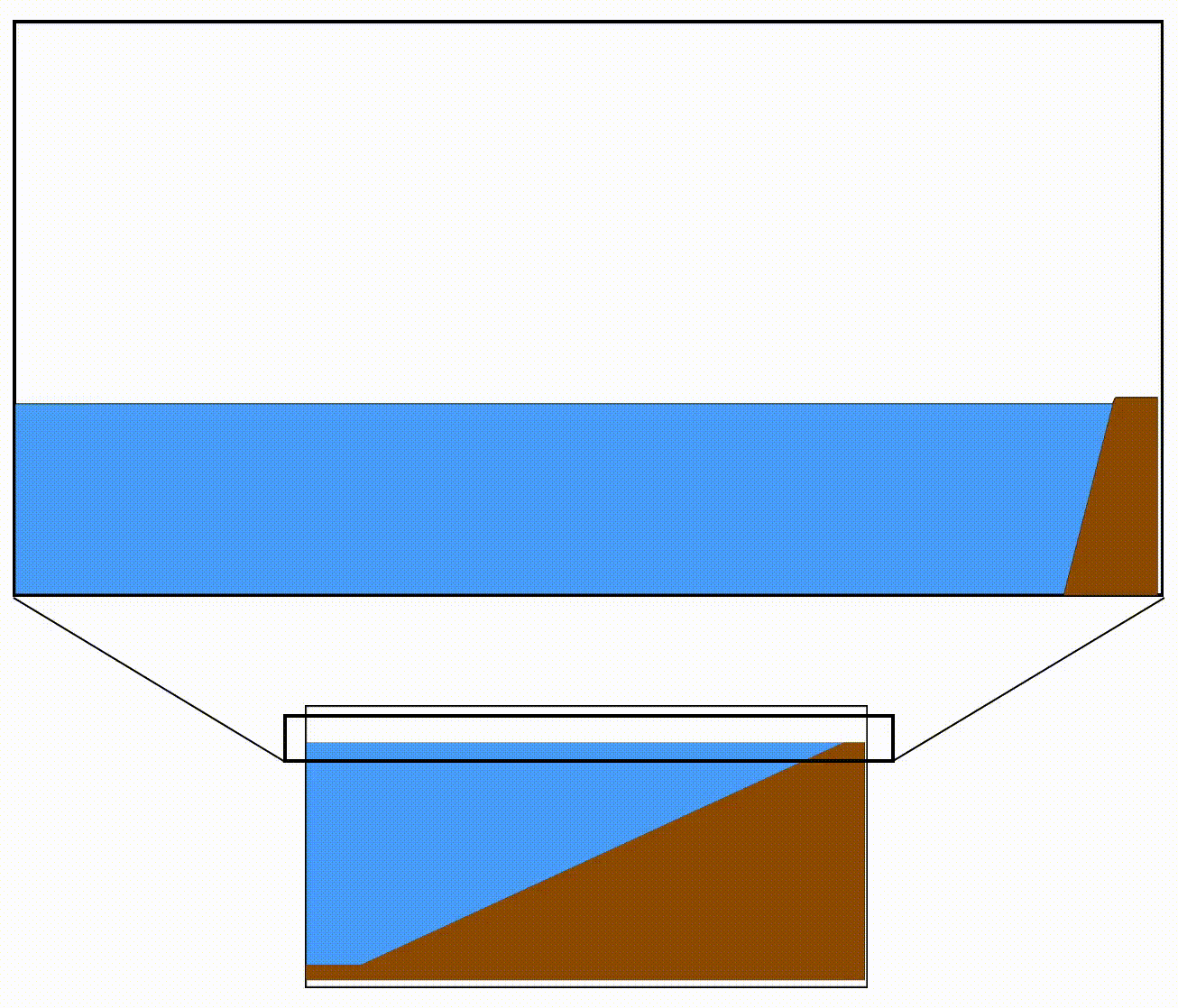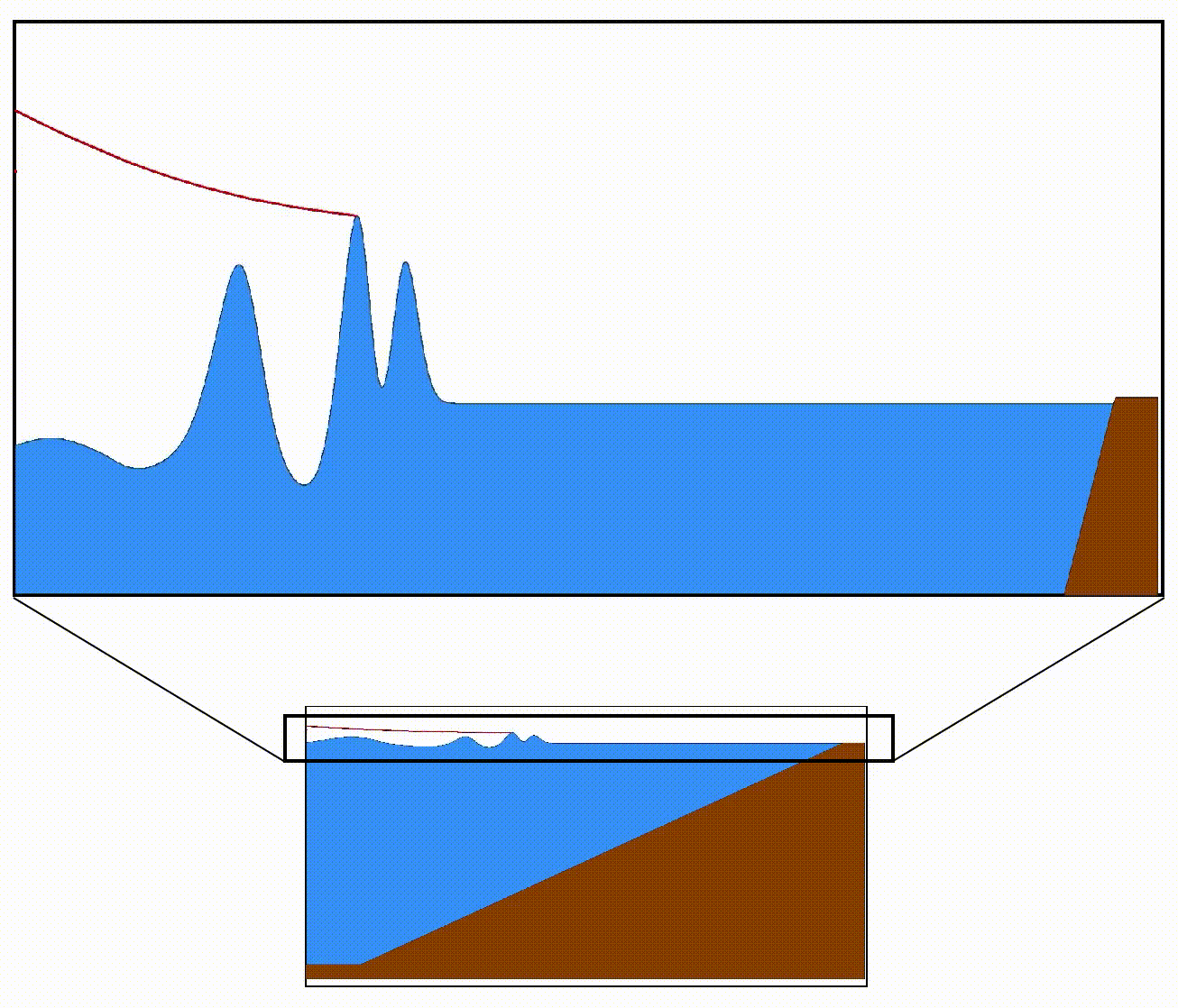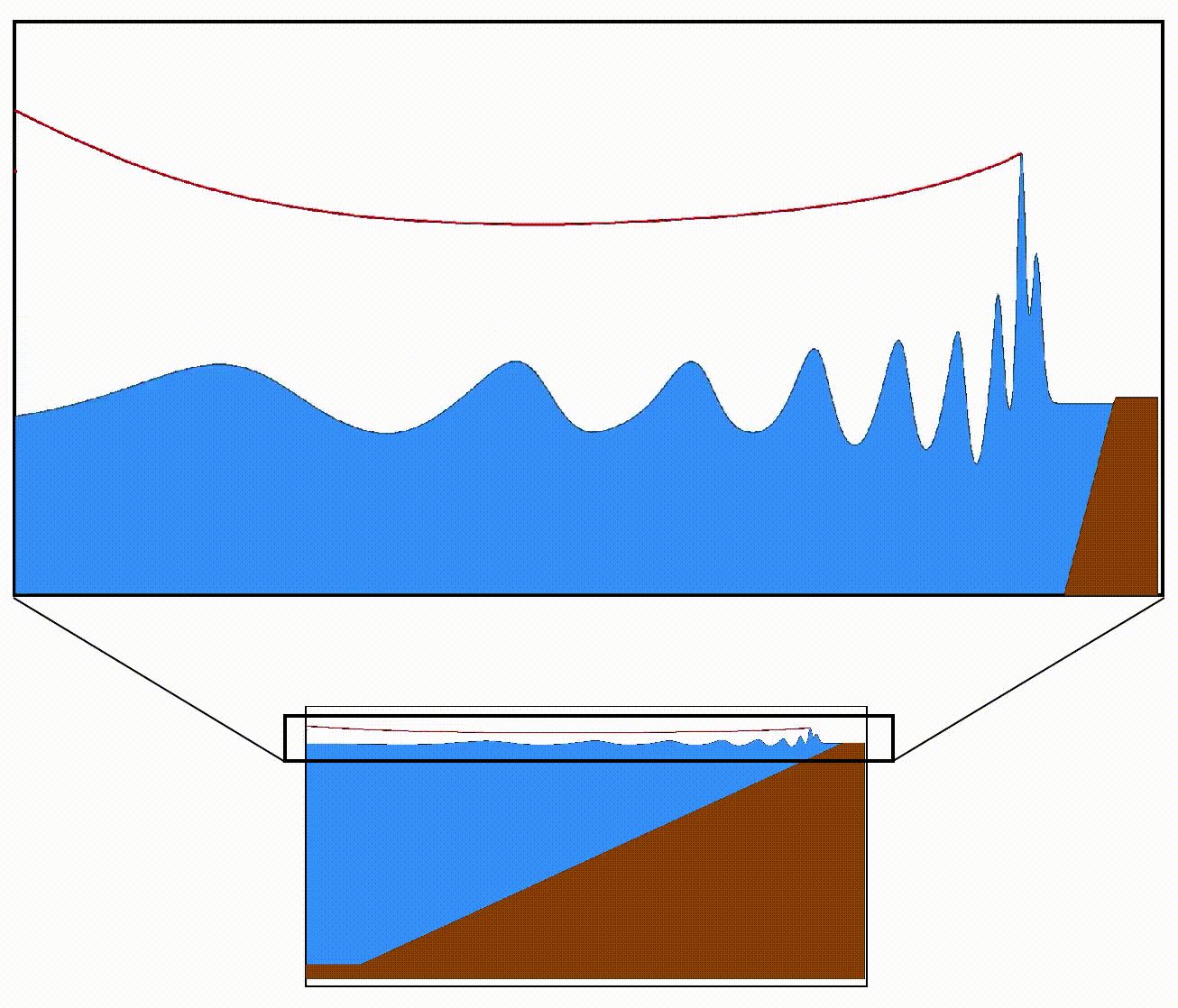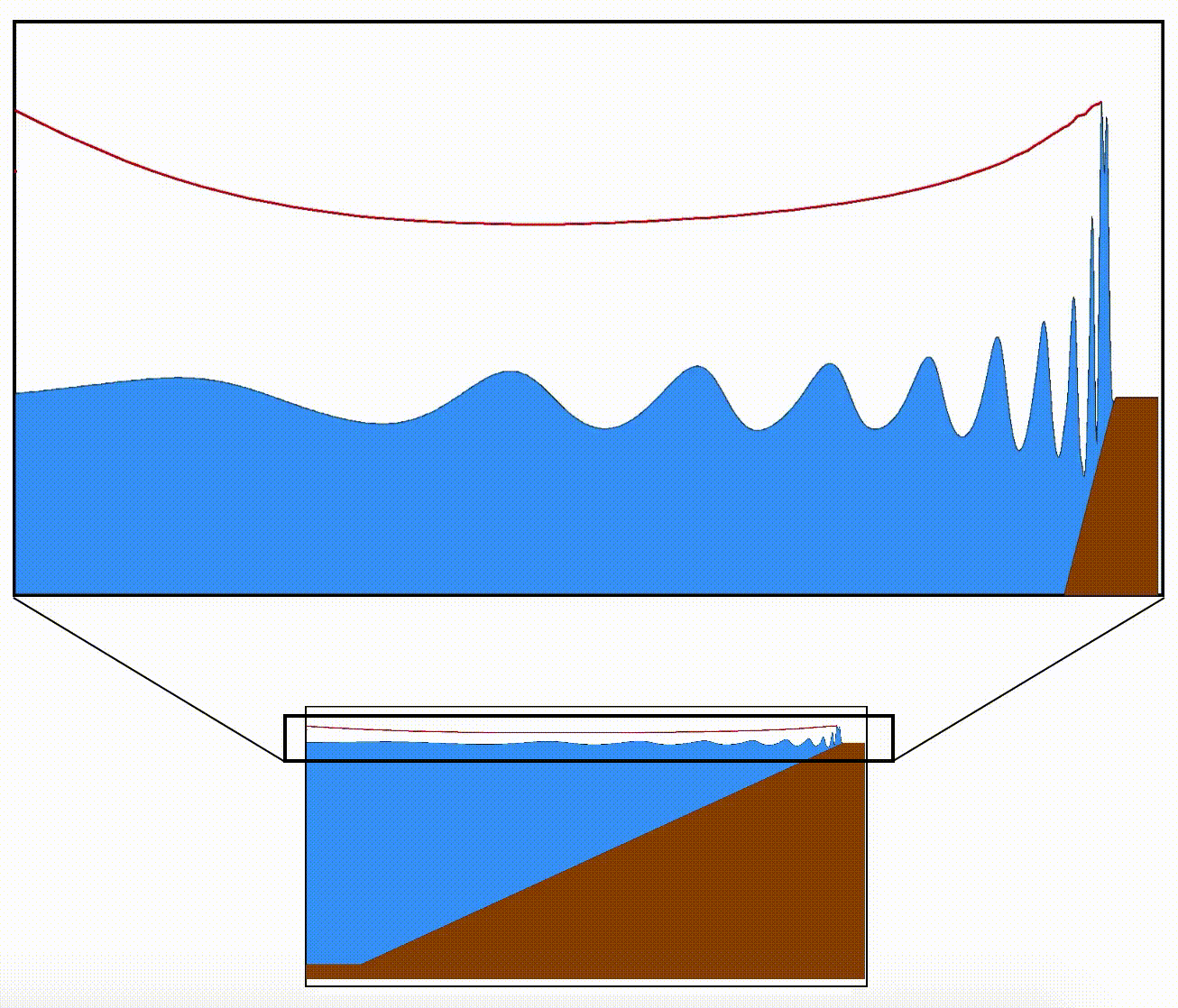
Here "X" shows the series length in miles, and the numbers attached to dashed lines are speed of each car. The red dashed line in the top panel is the constant initial"density" of cars.
If one of the cars in a series suddenly slows down or comes to a halt, the cars behind it who have not noticed the slowdown will be moving fast, until they too slow down and stop. As a result of this, the series will become very short and the cars will be accumulated in a smaller area. In the bottom panel, the red car in the front has slowed down and the rest of the cars which were equally spaced follow suit. As a result, the series becomes shorter (in a full pile-up the series will have a zero length). The blue curve on the top shows the density (accumulation) of cars in length, and as we expected it becomes larger and larger until the full pile-up (X=0 miles).
Note: In hydrodynamics, when a wave becomes very steep (in reality H/L > 1/7), it breaks. A similar (but not exactly the same) thing happens here: the density decreases in the end, since some of the cars pass the "X=0 mile" point.
Below is a cartoon showing the shoaling of tsunami waves from an earthquake in the left (outside the frame) on a coastal slope. The red curve follows the maximum wave amplitude. Note the initial decrease of amplitude as the waves move away from the source which is then followed by an increase in amplitude due to shoaling. Compare this movie to the top panel of the cartoon above.
This animated (gif) cartoon shows the effects of focal mechanism & depth of earthquakes on recorded seismic signals.
- Both panels are map views of epicenter with concentric circles at distances of 20, 25, and 30 degrees.. Waveforms are synthetic seismograms at eight azimuths for each distance.
- In both panels, the focal sphere is rotating by varying fault dip (δ) and slip (λ) while keeping the strike (φ) constant.
- The difference between the two panels is the hypocenter depth with the one on the right being deeper.
- Both panels use the same attenuation and velocity models (ak135).
- For a few suggestions on class activities using this cartoon, see here.

Shoaling of long waves (e.g. tsunamis):
Simply put, shoaling happens because the gravity waves slow down as they approach the coastline on the coastal slopes. The speed gradient at the front (slower) and back (faster) ends of a wave results in a shortening of the wave. Conservation of mass and momentum then dictate that the shortening is compensated by an increase in wave height.
A simple analogy of the shoaling process is traffic pile-up, as I have tried to show in the cartoon below:

Here "X" shows the series length in miles, and the numbers attached to dashed lines are speed of each car. The red dashed line in the top panel is the constant initial"density" of cars.
If one of the cars in a series suddenly slows down or comes to a halt, the cars behind it who have not noticed the slowdown will be moving fast, until they too slow down and stop. As a result of this, the series will become very short and the cars will be accumulated in a smaller area. In the bottom panel, the red car in the front has slowed down and the rest of the cars which were equally spaced follow suit. As a result, the series becomes shorter (in a full pile-up the series will have a zero length). The blue curve on the top shows the density (accumulation) of cars in length, and as we expected it becomes larger and larger until the full pile-up (X=0 miles).
Note: In hydrodynamics, when a wave becomes very steep (in reality H/L > 1/7), it breaks. A similar (but not exactly the same) thing happens here: the density decreases in the end, since some of the cars pass the "X=0 mile" point.
Below is a cartoon showing the shoaling of tsunami waves from an earthquake in the left (outside the frame) on a coastal slope. The red curve follows the maximum wave amplitude. Note the initial decrease of amplitude as the waves move away from the source which is then followed by an increase in amplitude due to shoaling. Compare this movie to the top panel of the cartoon above.

Page last updated on: 07/10/2025 05:10:03
