HOME
| RESEARCH
| PUBLICATIONS
|
ABOUT ME |
CONTACT | WHAT'S NEW? | CASSANDRA! |
فارسی | CHANNEL | OUTREACH | TEACHING | CV
Tsunami Propagation Uncertainties:
The uncertainties in the tusnami propagation algorithms is to some extent due to the efficiency and structure of simulation algorithms. Thus, as is customary in fluid mechanics, these algorithms are routinely benchmarcked via laboratory and field observations. However, tsunami simulations are often far from ideal, that is from exactly what happened in the real world. This is mostly due uncertainties in both the tsunami source and propagation medium, i.e., bathymetry.
Our knowledge of tsunami sources in any form (earthquake, landslide, atmospheric pressure gradient, etc), is never complete. For instance, in the case of earthquakes the entire extent of underwater faulting is never fully resolved. More importantly, in the case of megathrust events the constraints on earthquake size are sketchy, particularly in the few hours or even days after the earthquakes.
Bathymetry model (which strongly affect tsunami propagation) are estimates of the real world. This depends on the source scale as well as the target coastal resolution, but it is important to obtain the most accurate models for the best simulations.
However, two legitimate questions are:
- How can we quantify the source/bathymetry resolution effect?
- How much source/bathymetry resolution do we really need to reasonably predict the main propagation features?
A. Bathymetry Resolution
Since bathymetry (especially on the global scale) is distributed on a sphere (i.e., Earth), it is appropriate to use spherical harmonics to mathematically expand bathymetry. The individual terms of expansion, or Ylms represent eigenfunctions of Laplace's equation (l and m are called degree and order). In this formalism, -l ≤ m ≤ l and therefore, l is the dominant factor in determining resolution. In this fashion, l=0 corresponds to a flat ocean, and l=∞ represents the original field.
By expanding the bathymetry in the harmonics space and isolating various numbers, we can obtain smoothed bathymetry fields various levels of physical resolution.
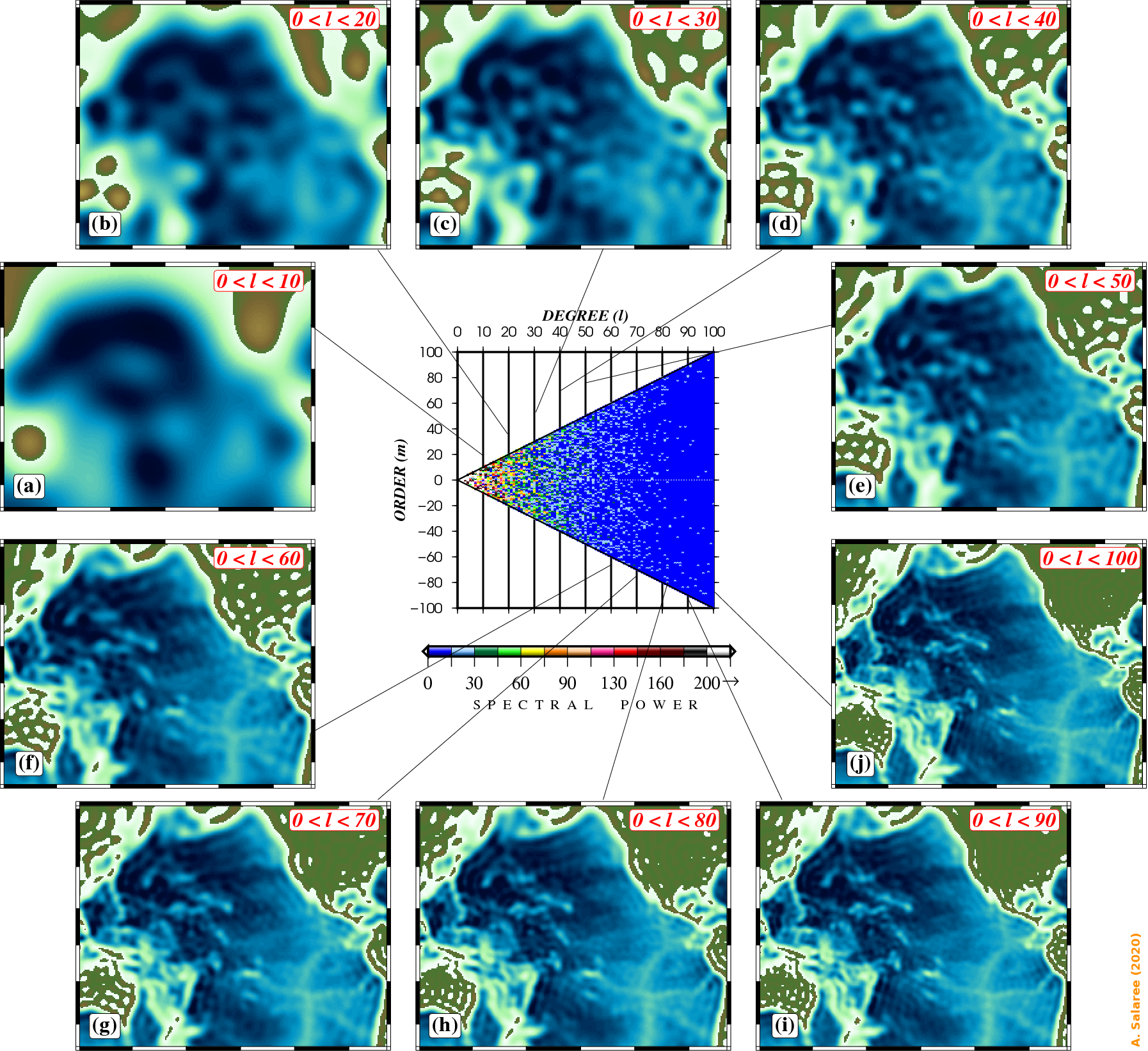
Various smoothed versions of the Pacific bathymetry obtained
by accumulating harmonic degrees (Salaree & Okal, 2020).
By simulating tsunamis at each resolution step, we gain insight into how physical resolution of bathymetry affects tsunami propagation. The figure below shows maximum tsunami wave heights calculated for each level of bathymetry resolution (see the figure above) for a M0=1029 dyn-cm, pure-thrust earthquake (φ=355, δ=15, λ=90) in Chile.

Maximum tsunami wave heights calculated for a pure-thrust at the epicenter
of the 2014 Iquique event simulated in various harmonic resolutions of
bathymetry. See the figure above (Salaree & Okal, 2020).
We can easily see that by adding to the maximum l used in bathymetry expansion, we get closer and closer to the real scenario. Using the MT parameter (Salaree, 2019) as the misfit between the smoothed simulation and the actual case, and more statistical analyses (such as the F-test), we can see that the l=40 (~1000 km) denotes the bathymetry resolution necessary to reproduce the main features necessary for a M0=1030 dyn-cm source.
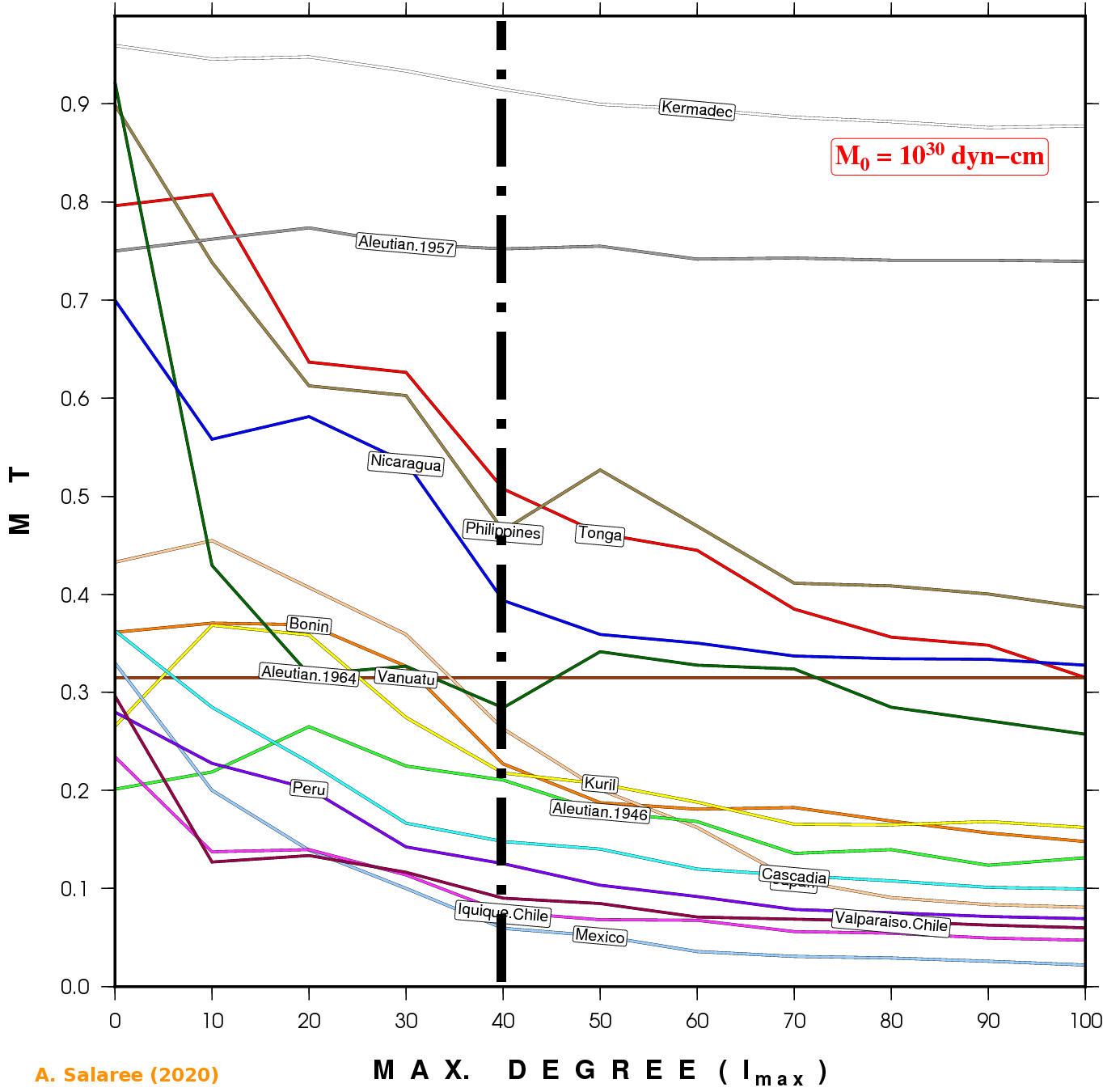
MT values calculated for pure-thrust events around the Pacific for smoothed
bathymetries against the "real" simulation in each case. We can see that
after l~40 there is not much change in MT (Salaree & Okal, 2020).
B. Source Resolution:
As tsunami sources are more localized compared to bathymetry, we can use a linear 2-D Fourier expansion to decompose them into their components.
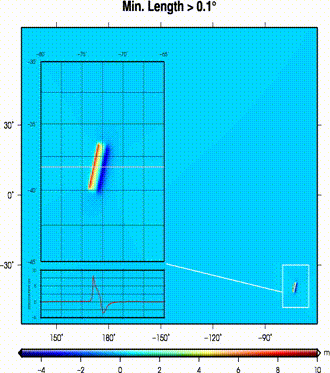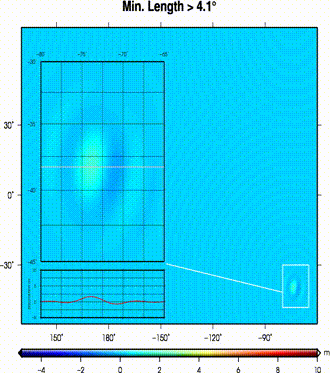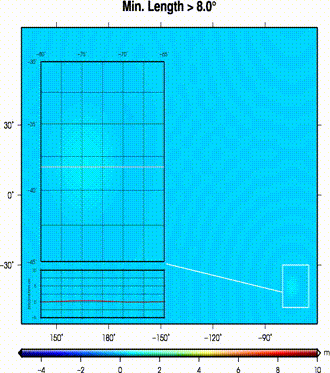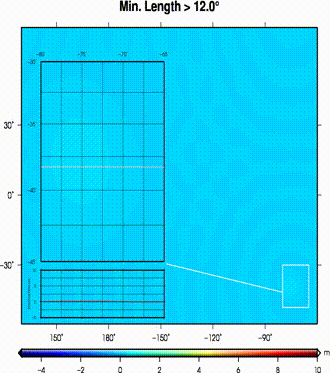
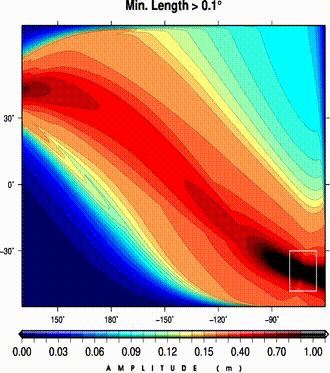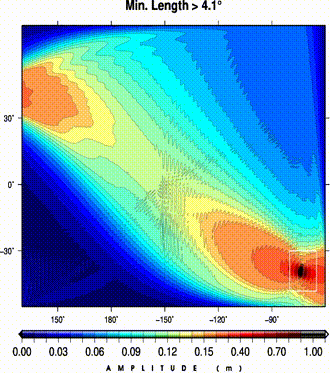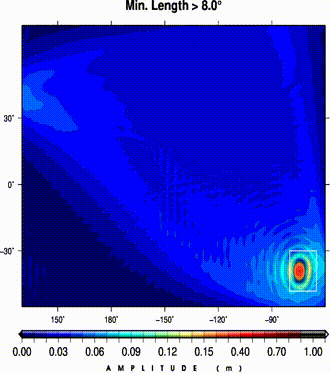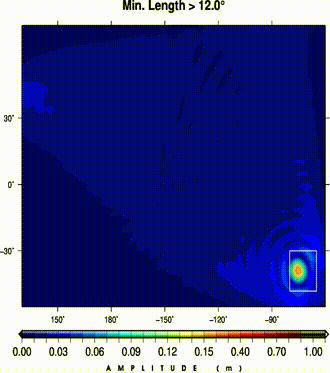
(left) A dislocation field from a pure thrust event in southeastern margins of a flat ocean.
The dislocation field is progressively smoothed by removing larger features (i.e., min. remaining length);
(right) at each step maximum tsunami wave heights are calculated.
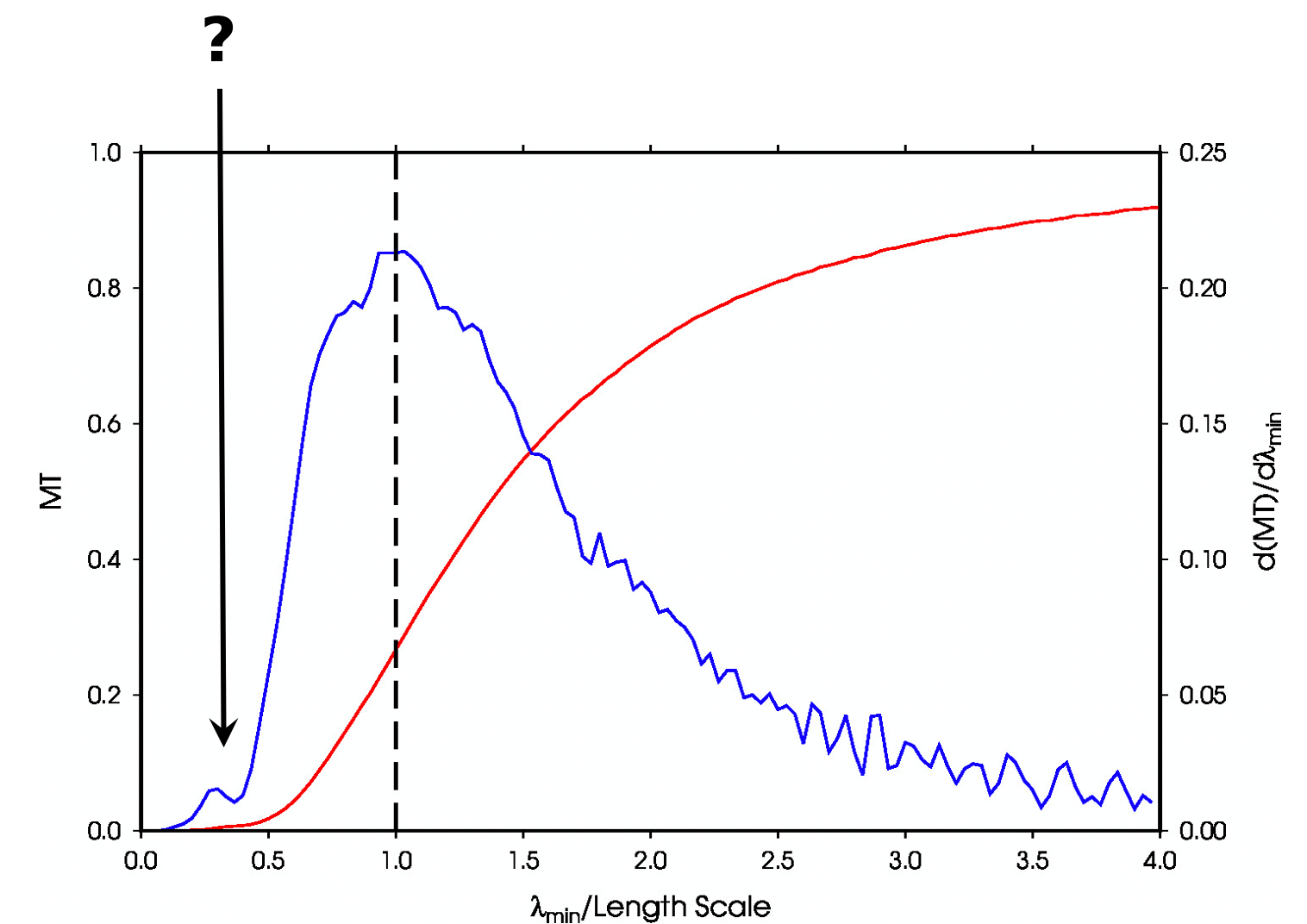
An analysis of MT values shows a local exteremum for the change in misfit.