Ok, I know it's shocking, but just keep reading...
So, how was the conformation of ketone 22 determined?
The conformation of the above ketone can be deduced by close examination of the coupling constants found in the HNMR. The two possible conformations are shown below. The hydrogen under consideration is marked in bold.
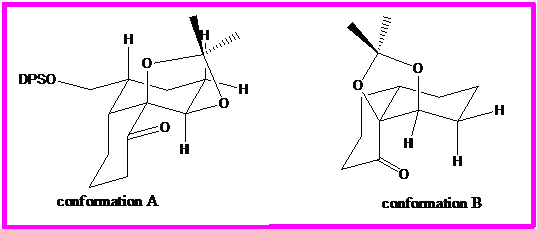
The bolded hydrogen has two 3-bond hydrogen neighbors. This means it will appear as a doublet of doublets or a triplet. Because it is part of a ring, there are two possible orientations for the hydrogen: axial or equatorial. In conformation A, it is axial, and in conformation b, it is equatorial.
There are also, therefore, two types of interactions that this hydrogen can have with other hydrogens on the ring. In conformation A it experiences axial-interaction with the axial hydrogen on the neighboring carbon. This signal would be expected to appear as a doublet of doublets, because the hydrogen would have two different coupling constants with each of its neighbors. In conformation B, it experiences only equatorial interactions. The coupling constants would be similar enough that the signal would probably appear as a triplet.
A review of Karplus' rule is useful here. Martin Karplus developed an equation which correlates the coupling constant seen in HNMR with the dihedral angle between two neighboring hydrogens. The closer the angle is to 90 degrees, the smaller the coupling constant will be. An increase or decrease of that angle results in a larger coupling constant.
So how does Karplus' equation apply to this example? The axial interaction between the hydrogens is another way of saying that their dihedral angle is 180 degrees. According to Karplus, that interaction will produce the largest coupling constant between vicinal hydrogens. Conversely, an equatorial dihedral angle is much closer to 90 degrees, so would have a small coupling constant.
The 1HNMR spectral data is provided by the authors in the article. The bolded hydrogen is assigned to the triplet at 4.12 ppm, with a coupling constant of 2.7 Hz. Such a low coupling constant indicates that the hydrogen was experiencing only equatorial interactions, and therefore the spectra was taken of the ketone in conformation B. Also, it is interesting to note that the hydrogen is much more downfield shifted than one would expect. A normal chemical shift for a hydrogen attached to an sp3 carbon which is bonded to an oxygen is around 3.8 ppm. However, due to the close proximity of the carbonyl, an electron-withdrawing inductive force acts on the hydrogen to deshield it.
So if conformation B is confirmed by 1HNMR data, why did the authors chose to show the structure in conformation A? Though the authors are not available for questioning, their reasoning probably has to do with the mechanism of reaction in the next step. The mechanism involves a nucleophilic attach of a carbon nucleophile (formed by Grignard reagent) on the carbonyl carbon. Let's take one more look at the structures:

The carbon nucleophile will attack the carbonyl from the axial direction. In conformation B, an axial attack is highly sterically hindered by the hydrogen substituents of the other ring. But hasn't conformation B already been identified by HNMR as the correct conformation?
A solution to this perplexing problem can be found by applying a well-known principle of reactivity in organic reactions. The Curtin-Hammett principle states that for a reaction which involves a pair of conformers (such as A and B above) and which results in two different products, the product ratio depends only on the difference in the energies of the transition states, and will not reflect the ratio of the original conformers at equilibrium. Applied to this reaction, it does not matter if conformation B is more present at equilibrium (a safe guess based on the HNMR data); if the energy of the transition state of the reaction of conformation A is LOWER than the energy of the transition state for conformation B, then the product of the reaction will be primarily from conformation A. Because of the large amount of steric hindrance for an axial nucleophilic attack at conformation B, it can be safely assumed that the transition state energy would be much higher than for compound A. And indeed, going back to the article, the product of the reaction is shown as the product of the reaction of conformation A.
The authors of the article presented us with what initially appeared as a contradiction. An axial nucleophillic attack will occur preferentially with conformation A, yet the spectral data points to the predominance of compound B at equilibrium. The important lesson to take away from this is the essence of the Curtin-Hammett principle: regardless of which conformation exists in majority at equilibrium, the reaction will progress in the direction of the lower-energy transition state.