Professional Reference Shelf

Competitive inhibition is of particular importance in pharmacokinetics (drug therapy). If a patient were administered two or more drugs simultaneously which react within the body with a common enzyme, cofactor, or active species, this could lead to competitive inhibition of the formation of the respective metabolites and produce serious consequences.

In this type of inhibition another substance, I, competes with the substrate for the enzyme molecules to form an inhibitor-enzyme complex, (EI). Typical steps in an enzymatic reaction of this type of inhibition are

	CD7.3 Enzyme Inhibition1 The maximum velocity, Vmax, in addition to being a function of the total enzyme concentration, may also be a function of other variables, such as ionic strength, pH, temperature, and inhibitor concentrations. For a number of enzymes Vmax exhibits an optimum in pH. (At a low pH the Vmax increases with increasing pH, while at a high pH it decreases with increasing pH, with the maximum value lying in the intermediate pH range.) One mathematical model that has been used to express this dependency on hydrogen ion concentration is.2
		(CD7-9)
	where H is hydrogen ion concentration and Ka and Kb are the ionization constants of the enzyme-substrate complex in the acidic, and basic solutions, respectively. The denominator of Equation (CD7-9) is referred to as the Michaelis pH function. The Michaelis constant, Km has been observed to exhibit a similar dependence on pH. In addition to pH, another factor that greatly influences the rates of enzyme-catalyzed reactions is the presence of an inhibitor. The most dramatic consequences of enzyme inhibition are found in living organisms, where the inhibition of any particular enzyme involved in a primary metabolic sequence will render the entire sequence inoperative, resulting in either serious damage or death of the organism. For example, the inhibition of a single enzyme, cytochrome oxidase, by cyanide will cause the aerobic oxidation process to stop; death occurs in a very few minutes. There are also beneficial inhibitors such as the ones used in the treatment of leukemia and other neoplastic diseases. The three most common types of reversible inhibition occurring in enzymatic reactions are competitive, uncompetitive, and noncompetitive. The enzyme molecule is analogous to the heterogeneous catalytic surface in that it contains active sites. When competitive inhibition occurs, the substrate and inhibitor are usually similar molecules that compete for the same site on the enzyme. Uncompetitive inhibition occurs when the inhibitor deactivates the enzyme-substrate complex, usually by attaching itself to both the substrate and enzyme molecules of the complex. Noncompetitive inhibition occurs with enzymes containing at least two different types of sites. The inhibitor attaches only to one type of site and the substrate only to the other.
	CD7.3A Competitive Inhibition
		(CD7-10)
	Example CD7-3 Derive a Rate Law For Competitive Inhibition
	CD7.3B Uncompetitive Inhibition
	Here, the inhibitor does not compete with the substrate for the enzyme; instead, it ties up the enzyme-substrate complex by forming an inhibitor-enzyme-substrate complex, thereby restricting the breakdown of the (ES) complex to produce the desired product. Typical steps in an uncompetitive enzymatic reaction are
	The rate of formation of the product is
		(CD7-12)
	Application of the pseudo-steady-state hypothesis to ES and IES yields the respective equations
		(CD7-13) (CD7-14)
	To obtain ES, we solve Equations (CD7-12) and (CD7-14) together with the mole balance for the total enzyme initially present,
		(CD7-15)
	and substitute the result into Equation (7-49) to obtain the rate law for the mechanism above, involving the uncompetitive inhibition of an enzymatic reaction:
		(CD7-16)
	A Lineweaver-Burk plot of Equation (CD7-16) for different inhibitor concentrations will result in a family of parallel lines all with a slope of Km/Vmax.
	CD7.3C Noncompetitive Inhibition In noncompetitive inhibition, the substrate and inhibitor molecules react with different types of sites on the enzyme molecule, and consequently, the deactivating complex, IES, can be formed by two reversible reaction paths: 1. After a substrate molecule attaches to the enzyme molecule at the substrate site, the inhibitor molecule attaches to the enzyme at the inhibitor site. 2. After an inhibitor molecule attaches to the enzyme molecule at the inhibitor site, the substrate molecule attaches to the enzyme at the substrate site. These paths, along with the formation of the product, P. are as follows:
	This reaction sequence can also be written as

	Reaction 1	E + SES	(CD7-17)
	Reaction 2	E + IIE	(CD7-18)
	Reaction 3	I + ESIES	(CD7-19)
	Reaction 4	IE + SIES	(CD7-20)
	Reaction 5	ESP + E	(CD7-21)

	An alternative method of finding the rate law for the sequence presented in Equations (CD7-17) through (CD7-21) is to assume that the last reaction, (CD7-21), is rate limiting and that each of the other reactions, (CD7-17) through (CD7-20), is essentially in equilibrium. This method is analogous to that used to derive the rate law in heterogeneous catalysis, where one of the steps (e.g., adsorption) is rate controlling. Assuming that the rate-limiting step (reaction 5) is irreversible, the rate of formation of the product is
	rp = kp(ES)	(CD7-22)
	Using this equilibrium technique, the rate law for the first reaction, Equation (CD7-17),
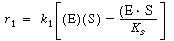
		(CD7-23)
	is rearranged and the ratio of the rate of reaction to the specific reaction rate is set equal to zero.
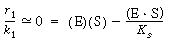
	The resulting equation is solved for the concentration of the enzyme-substrate complex.
	(ES) =Ks(S)(E)	(CD7-24)
	Example CD7-4 Derive a Rate Law For Non-Competitive Inhibition
	Since the substrate and inhibitor attach at different sites, a reasonable assumption is that the equilibrium between the enzyme and the substrate is the same whether or not an inhibitor is attached to the enzyme (i.e., Ks =); then
	(EIS) = Ks(EI)(S)
	and
	(ES) = Ks(E)(S)
	By making a similar assumption for the equilibrium between the enzyme and the inhibitor, KI =, we can rearrange Equation (CDE7-4.6) so that
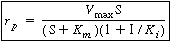
		(CD7-25)
	where
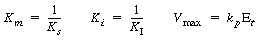
	Equation (CD7-25) is in the form of the rate law that is usually given for an enzymatic reaction exhibiting noncompetitive inhibition. Heavy metal ions such as Pb2+, Ag+, Hg2+, and others, as well as inhibitors that react with the enzyme to form chemical derivatives, are typical examples of noncompetitive inhibitors. The various types of inhibition are compared with a reaction in which no inhibitors are present (dark line) on the Lineweaver-Burk plot shown in Figure CD7-1. We observe the following relationships: 1. In competitive inhibition the slope increases with increasing inhibitor concentration while the intercept remains fixed. 2. In uncompetitive inhibition the y-intercept increases with increasing inhibitor concentration while the slope remains fixed. 3. In noncompetitive inhibition both the intercept and slope will increase with increasing inhibitor concentration.

Figure CD7-1
	In addition to the Lineweaver-Burk plot, the Eadie plot is also used to present data of enzymatic reactions. The Eadie plot magnifies departures from linearity that might not be observed in the Lineweaver-Burk plot. In Figure CD7-2a, b, and c, the Eadie plot is used to present the data for three enzymatic reactions: one with the competitive type of inhibition, one with the uncompetitive type of inhibition, and the third with the noncompetitive type of inhibition. Each figure contains two lines corresponding to two different inhibitor concentrations; line a represents the higher inhibitor concentration and line b the lower inhibitor concentration.
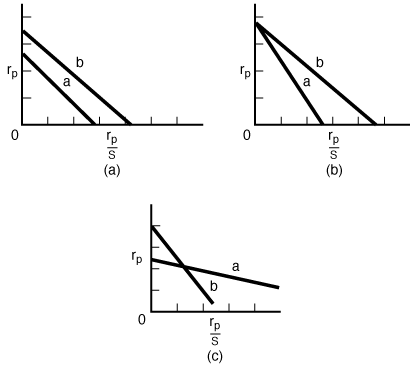
Figure CD7-2
Example CD7-5 Match Eadie Plots to the Different Types of Inhibition Next