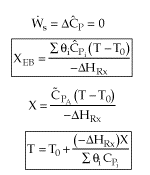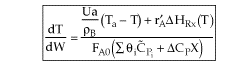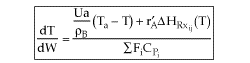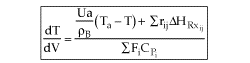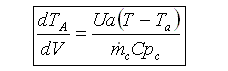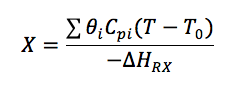Chapter 11: Nonisothermal Reactor Design: The Steady State Energy Balance and Adiabatic PFR Applications

Topics

Why Use the Energy Balance?
Overview of User Friendly Energy Balance Equations
Manipulating the Energy Balance, DHRx
Reversible Reactions
Adiabatic Reactions
Interstage Cooling/Heating

Energy Balances, Rationale and Overview

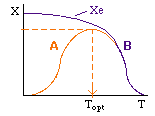
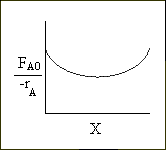
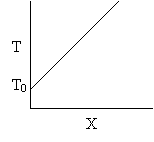
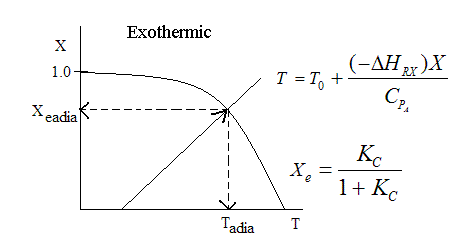
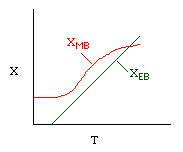
Reaction YouTube Video: Nitrogen Triiodide

Let's calculate the volume necessary to achieve a conversion, X, in a PFR for a first-order, exothermic reaction carried out adiabatically. For an adiabatic, exothermic reaction the temperature profile might look something like this:

The combined mole balance, rate law, and stoichiometry yield:

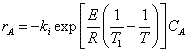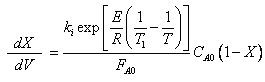To solve this equation we need to relate X and T.

We will use the Energy Balance to relate X and T. For example, for an adiabatic reaction, e.g.,, in which no inerts the energy balance yields

We can now form a table like we did in Chapter 2,

User Friendly Energy Balance Equations

top

The user friendly forms of the energy balance we will focus on are outlined in the following table.

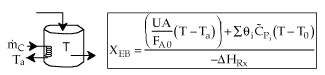
User friendly equations relating X and T, and F_i and T

1. Adiabatic CSTR, PFR, Batch, PBR achieve this:

(1.A)

(1.B)

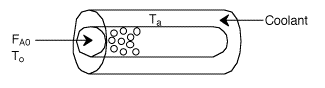
2. CSTR with heat exchanger, UA(T_a-T) and large coolant flow rate.

(2)

3 . PFR/PBR with heat exchange

3A. In terms of conversion, X

(3.A)

3B. In terms of molar flow rates, F_i

(3.B)

4. For Multiple Reactions

(4)

5. Coolant Balance

Co-Current Flow

(5)

These equations are derived in the text. These are the equations that we will use to solve reaction engineering problems with heat effects.

Energy Balance

top

In the material that follows, we will derive the above equations.

Energy Balance:

Typical units for each term are J/s; i.e. Watts James Prescott Joule (1818-1889) James Watt (1736-1819)

(1) OK folks, here is what we are going to do to put this above equation into a usable form. Replace E_i by E_i=H_i-PV_i Express H_i in terms of enthalpies of formation and heat capacities Express F_i in terms of either conversion or rates of reaction Define DH_RX Define DC_P Manipulate so that the overall energy balance is either in terms of the User Friendly Equations (yellow box) 1.A, 1.B, 2, 3A, 3B, or 4 depending on the application
Step 1: Substitute
, , and
into equation (1) to obtain the General Energy Balance Equation.
General Energy Balance:

For steady state operation:

We need to put the above equation into a form that we can easily use to relate X and T in order to size reactors. To achieve this goal, we write the molar flow rates in terms of conversion and the enthalpies as a function of temperature. We now will "dissect" both F_i and H_i. [Note: For an animated derivation of the following equations, see the Interactive Computer Modules (ICMs) Heat Effects 1 and Heat Effects 2.]

Flow Rates, F_i
For the generalized reaction:
In general,

Enthalpies, H_i Assuming no phase change:




Mean heat capacities:




Energy Balance with "dissected" enthalpies:

For constant or mean heat capacities:

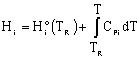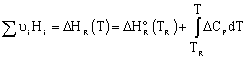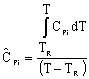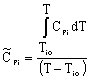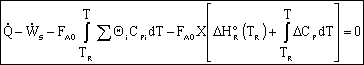Adiabatic Energy Balance:

Adiabatic Energy Balance for variable heat capacities:
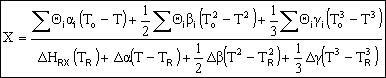
For constant heat capacities: We will only be considering constant heat capacities for now.

Reversible Reactions

top

Consider the reversible gas phase elementary reaction.

The rate law for this gas phase reaction will follow an elementary rate law.

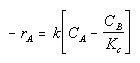
Where K_c is the concentration equilibrium constant. We know from Le Chaltlier's Law that if the reaction is exothermic, K_c will decrease as the temperature is increased and the reaction will be shifted back to the left. If the reaction is endothermic and the temperature is increased, K_cwill increase and the reaction will shift to the right.

at equilibrium

$$ -r_{A} = 0 $$

$$ K_{c} = \frac{C_{B\beta}}{C_{A\beta}} = \frac{C_{A0}X_{\beta}{\frac{T_{0}}{T}}p}{C_{A0}(1 - X_{\beta}){\frac{T_{0}}{T}}p} = \frac{X_{\beta}}{1 - X_{\beta}}$$

$$ X_{\beta} = \frac{K_{c}}{1+K_{c}} $$

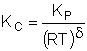
	Van't Hoff Equation

For the special case of: Integrating the Van't Hoff Equation gives:

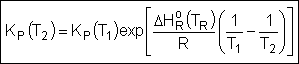
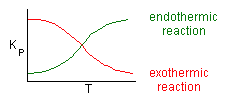
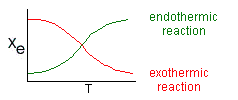
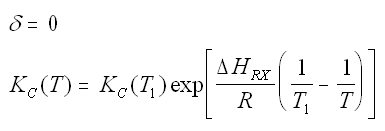
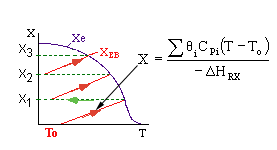
Adiabatic Equilibrium

Conversion on Temperature

Exothermic ΔH is negative

Adiabatic Equilibrium temperature (T_adia) and conversion (X_eadia

Endothermic ΔH is positive

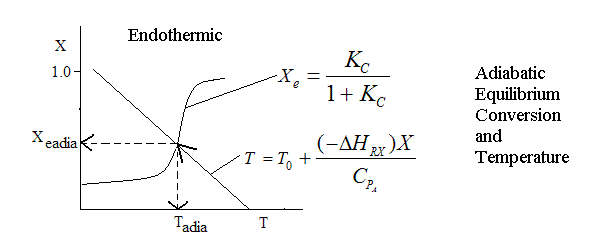
Adiabatic Reactions

top

Van't Hoff

Algorithm Adiabatic Reactions:

Suppose we have the Gas Phase Reaction

that follows an elementary rate law. To generate a Levenspiel plot to size CSTRs and PFRs we use the following steps or as we will see later use POLYMATH.

1. Choose X
Calculate T
Calculate k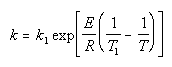
Calculate K_C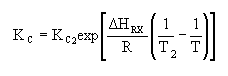
Calculate T_o/T
Calculate C_A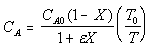
Calculate C_B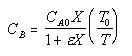
Calculate -r_A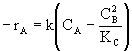
2. Increment X and then repeat calculations.
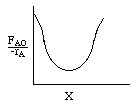3. When finished, plotvs. X or use some numerical technique to find V.
Levenspiel Plot for an exothermic, adiabatic reaction. Reactor Sizing We can now use the techniques developed in Chapter 2 to size reactors and reactors in series to compare and size CSTRs and PFRs.
Consider: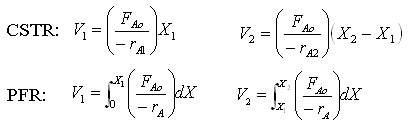

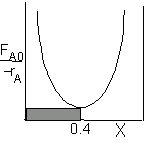
PFR Shaded area is the volume.
For an exit conversion of 40%	For an exit conversion of 70%

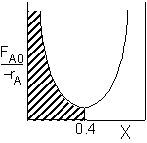
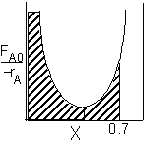
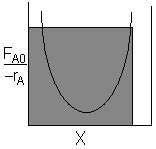
CSTRShaded area is the reactor volume.
For an exit conversion of 40%	For an exit conversion of 70%

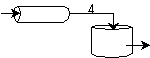
We see for 40% conversion very little volume is required. CSTR+PFR

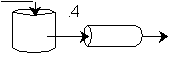
(a)	(b)
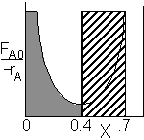
For an intermediate conversion of 40% and exit conversion of 70%

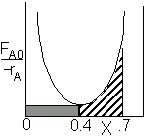
(a)	(b)

Looks like the best arrangement is a CSTR with a 40% conversion followed by a PFR up to 70% conversion.

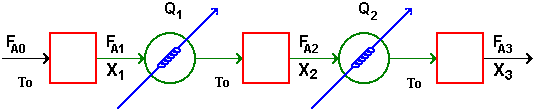
Interstage Cooling/Heating

top

Curve A: Reaction rate slow, conversion dictated by rate of reaction and reactor volume. As temperature increases rate increases and therefore conversion increases. Curve B: Reaction rate very rapid. Virtual equilibrium reached in reaction conversion dictated by equilibrium conversion.
Optimum Inlet Temperature: Fixed Volume Exothermic Reactor
Interstage Cooling:

Interstage Cooling Calculations in terms of x and x'

CSTR Algorithm

1.)	Given X Find T and V Solution: Linear progression of calc T cal k calc K_C calc -r_A calc V Adiabatic Liquid Phase in A CSTR
2.)	Given T Find X and V Solution: Linear progression: calc k cal K_C calc X calc -r_A calc V Adiabatic Liquid Phase in A CSTR
3.)	Given V Find X at T Solution: plot X_EB vs. T and X_MB vs. T on the same graph: