Introduction

Now, we consider the case when antivenom is injected into the victim's body just after being bit by the snake. This changes our initial condition for concentration of antivenom at t=0. Below are the equations used for case 2 which gives the behavior in next 5 hours of the cobra bite, when an appropriate amount of antivenom has been injected into the victim's body.

Determining the Appropriate Amount of Antivenom

Again, there is a catch here! How do we know the appropriate amount of antivenom that needs to be injected into the victim? We actually would need to work backwards. Run the polymath code above guessing different values of Ca(0) and select an optimum value which would save the life of the person in the long run (ie model the behavior for next 24 hours of the snake bite)

The required concentration of antivenom, C_a(0) was found to be 9*10^-9 mol/dm³. Assuming the volume of blood in the human body to be 40 dm³, we need to inject 3.6*10^-7 moles of antivenom into the body. A cobra bite injects around 2*10^-7 moles of venom into the body. Its effect can be counteracted by a lesser amount of antivenom. Also the time of administration of the antivenom is important,which we'll explore next in Case 3!

Receptor Sites Analysis

The equations we'll enter into Polymath are based on the additional information given in the problem statement and the equations derived earlier.

Polymath Code and Results

Our Polymath code for Case 2 can be downloaded using the link below.

Download the Code (.pol)

Let's take a look at the resulting plot of the fraction of free sites versus time:

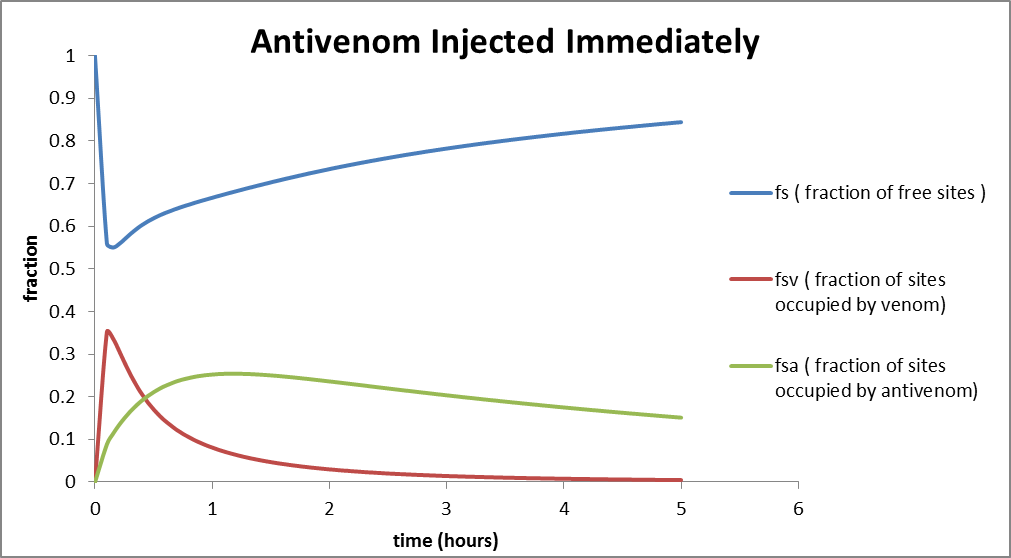
From the graph, we see that the fraction of free sites never drops below 0.6 and then eventually rises. Thus prompt injection of an appropriate amount of antivenom ensures the safety of the victim. The fraction of sites occupied by venom drops down to zero within five hours of the drug being administered. Also the fraction of sites occupied by antivenom rises and then drops down gradually.

It looks like our snake-bite victim will recover just fine.

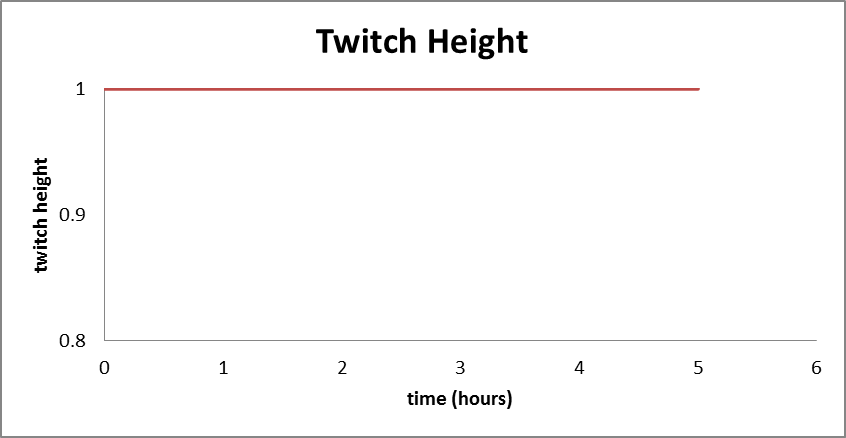
Twitch Height Analysis

We will now analyze how twitch height varies with time when an injection of antivenom is administered right when a cobra bites. To compute the values of twitch height, we will generate values of f_sv and f_sa from Polymath then copy the values to a spreadsheet. The twitch height is then computed using Equation E-40.

Code and Results

Our Polymath code for the Twitch Height Analysis for Case 2 can be downloaded using the link below.

Download the Code (.pol)

As we see in the graph, the twitch height remains close to one and the respiration system of the victim is expected to function normally throughout the duration.