Chapter 2: Conversion and Reactor Sizing
Numerical Evaulation of an Integral
Consider the liquid phase reaction
which is to take place in a PFR. The following data was obtained in a batch reactor.
X
0
0.4
0.8
-rA(mol/dm3.s) 0.01 0.008 0.002
If the molar feed of A to the PFR is 2 mol/s, what PFR volume is necessary to achieve 80% conversion under identical conditions as those under which the batch data was obtained?
(1) What is the PFR design equation and how should the data be plotted?$\dfrac{dF_A}{dt} = r_AV$
$V=\int_{0}^{X}\dfrac{F_{A0}dX}{-r_A}$
$V = \int_{0}^{X}\dfrac{F_{A0}dX}{r_A}$
(2) How can you evaluate the design equation?
$-r_A$ as a function of X
$\dfrac{1}{-r_A}$ as a function of X
$\dfrac{X}{-r_A}$ as a function of X
(3) What is the Simpson's three-point formula for numbered integration?
Hint 1
FA0 = 2 mol/s, fed to a plug flow reactor
(a) PFR $\therefore V = F_{A0}\int_{0}^{X}\dfrac{1}{-r_A}dX = \int_{0}^{X}\dfrac{F_{A0}}{-r_A}dX$
(b) Thus, one needs (1/-rA) as a function of X
Part (c)
$V=F_{A_0}\int_{0}^{X}\dfrac{1}{-r_A}dX=\dfrac{\Delta X}{3}\Big{[}\dfrac{1}{-r_A(X=0)} + \dfrac{4}{-r_A(X=0.4)} + \dfrac{1}{-r_A(X=0.8)}\Big{]}$
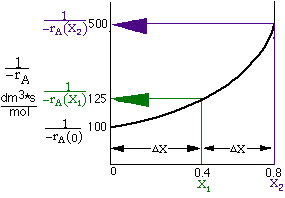
You can either take the area under the curve and multiply by FA0 or you can use one of the formulas in Appendix A.4.
Solution
FA0 = 2 mol/s, fed to a plug flow reactor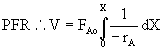
Thus, one needs (1/-rA) as a function of X

You can either take the area under the curve and multiply by FA0 or you can use one of the formulas in Appendix A.4.
For Simpson's three point formula we have:
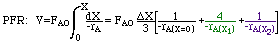
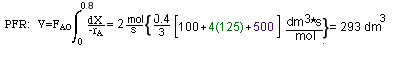
To reach 80% conversion, your PFR must be 293.3 dm3.
