Chapter 3: Rate Laws
Transition State Theory
Derivation of qTx
We will assume that the energy states are sufficiently close together, such that there is a continuous distribution of energies. Replace Σ with ∫
![]()
Let: ![]()
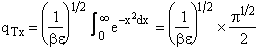
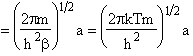 |
(T10) |
For 3-D
The translation partition function for y and z directions are similar to that for qTx
| This is the result we have been looking for! | 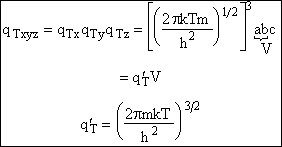 |
(T11) |
We define Λ as thermal wave length
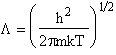 (m) (m) |
(T12) |
![]()
Order of Magnitude and Representative Values
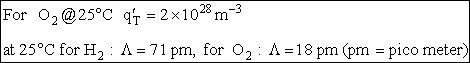
Return to Derivation of Translational Partition Function