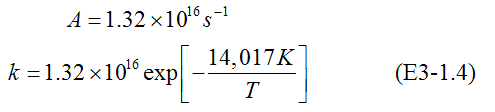Chapter 3: Rate Laws
Determination of the Activation Energy
This is Example 3-1 from the book page 95.Calculate the activation energy for the decomposition of benzene diazonium chloride to give chlorobenzene and nitrogen:
using the information in Table E3-1.1 for this first order reaction.
Solution
Solution
We start by recalling Equation (3-20)

We can use the data in Table E3-1.1 to determine the activation energy, E, and frequency factor, A, in two different ways. One way is to make a semilog plot of k vs. (1/T) and determine E from the slope. Another way is to use Excel or Polymath to regress the data. The data in Table E3-1.1 was entered in Excel and is shown in Figure E3-1.1 which was then used to obtain Figure E3-1.2.
A step-by-step tutorial to construct both an Excel and a Polymath spread sheet is given in the Chapter 3 Summary Notes on the CD-ROM.
(a)Graphical Solution
Figure E3-1.2(a) shows the semilog plots from which we can calculate the activation energy. From CD-ROM Appendix D, we show how to rearrange Equation (3-20) in the form
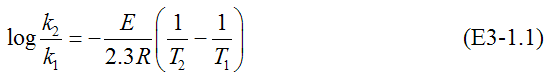
Rearranging
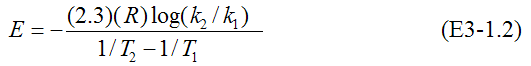
To use the decade method, choose 1/T1 and 1/T2 so that k2= 0.1k1. Then, log(k1/k2)=1.
When k1 = 0.005: 1/T1 = 0.003025 and when k2= 0.0005: 1/T2 = 0.00319
Therefore,
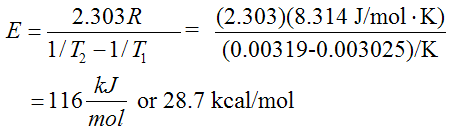
From Figure E3-1.2(b) and Equation (E3-1.3), we see
ln A = 37.12
taking the antilog