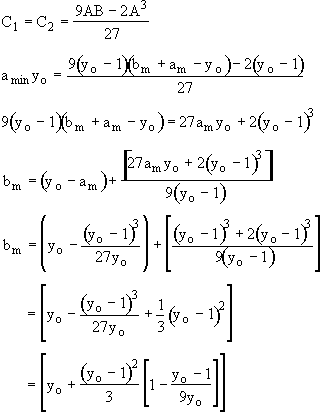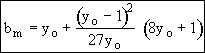Chapter 9: Reaction Mechanisms, Pathways, Bioreactions and Bioreactors
Bifurcation Analysis
Substrate Inhibited Enzyme Reactions in a CSTR
Problem Statement
A substrate inhibiting enzyme reaction
![]()
is carried out in a CSTR with residence time t. The inlet concentration of the substrate is CSO and the rate law is defined as
![]() (1)
(1)
a) Reduce the material balance to show that
![]() (2)
(2)
where
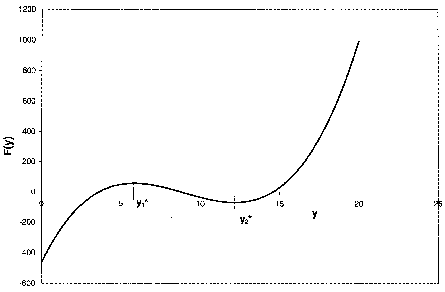
y = KI CS
yo = KI CSO
a = Km KI
b = t Vmax KI
What is the maximum number of multiple steady states possible?
b) Let A = yo – 1 , B = a + b – yo , C = yo a
Show Eqn (2) can be put in the form
![]() (3)
(3)
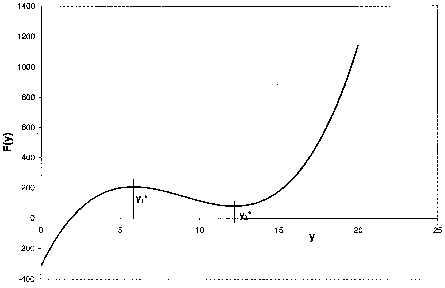
c) Plot F(y) as a function of y (e.g. choose A=9, B=10, C=5.) Assuming the shape of the curve remains the same, sketch what happens as one varies A, B and C. Using the solution to (b), show the maximum and minimum points in F(y) occur at
![]() (4)
(4)
and that y1 and y2 are positive and real if
![]() (5)
(5)
![]() (6)
(6)
d) Discuss the fact that multiple steady states will occur if
![]() (7)
(7)
e) Show that multiple steady states can exist only if
(a + b) > yo > 1 (8)
![]()
and
27 C2 – 18 ABC – A2B2 + 4A3C + 4B3 < 0 (9)
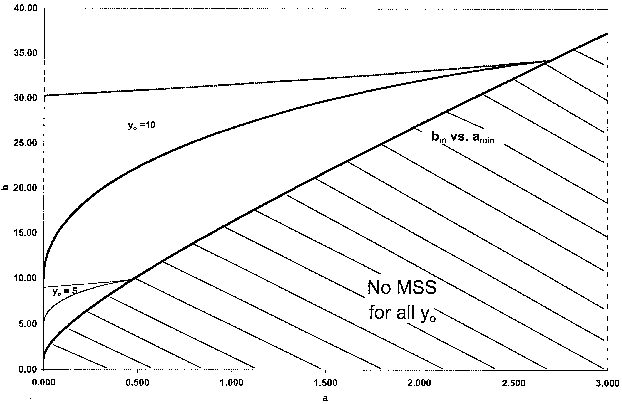
f) For yo = 10, show the region of multiple steady states on a plot of “b” as a function of “a”. Hint: First use Polymath to find C and a function of B
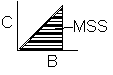 [Not to scale or shape]
[Not to scale or shape]
What is the minimum value of “a” above which there will always be only one steady state? How will this minimum value of “a” change when yo is changed?
g) Develop a rough map to show
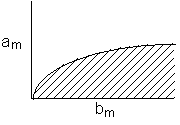
h) For very high substrate concentrations, what is the maximum number of multiple steady states possible? Show the region of MSS on a plot of b as a function of yo.
Hint: For high CS: ![]()
Solution:
Part a) CSTR Material Balance
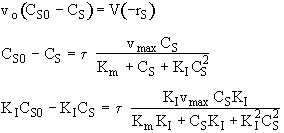
![]()
where
![]()
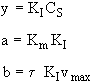
![]()
![]()
![]()
![]()
Because this is a cubic equation, three steady states are possible
Part b)
A = yo - 1
B = a + b - yo
c = yoa
![]()
![]()
Part c)
@ y*
![]()
![]()
![]()
Part d)
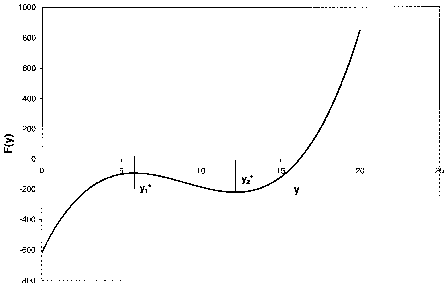
We need to find the condition when the above equation has three positive roots. Hence, graphically F(y) should be
![]()
If F(y) is such that
Case I
![]()
Case II
![]()
Part e)
Then there is only one real positive real root to F(y) = 0. Let’s assume that the points where
F'(y) = 0
are ![]() and
and ![]()
For F(y) = 0 to have two positive real roots
![]() > 0 ,
> 0 , ![]() > 0
(1)
> 0
(1)
and
![]() < 0
(2)
< 0
(2)
F'(y) = -3 y2 - 2Ay + B = 0
![]()
![]()
![]()
For (1) i.e. ![]() > 0 and
> 0 and ![]() > 0
> 0
![]()
and
![]()
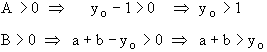
![]() (3)
(3)
For (2) i.e. ![]()
![]()
![]()
![]()
![]()
Here,
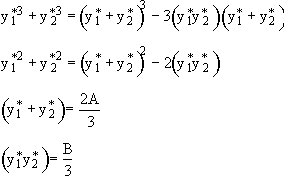
![]() (4)
(4)
Using Maple
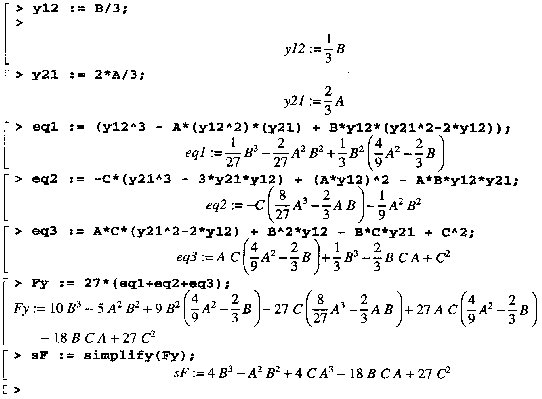
Hence (A) and (B) are the conditions for F(y) = 0 to have three positive real roots, i.e., three multiple steady states.
For multiple steady states
![]() (5)
(5)
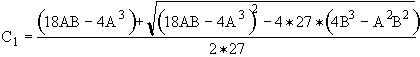 (6)
(6)
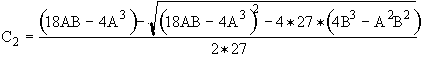 (7)
(7)
For condition (1) to hold
C1 ≤ C ≤ C 2
For yo = 10
A = 9
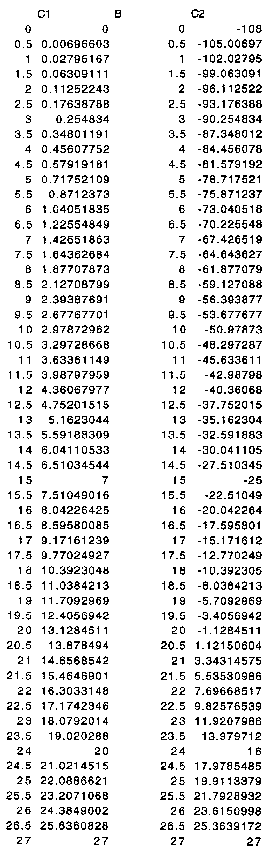
First compute C1 and C2 for various values of B as shown in Table 1
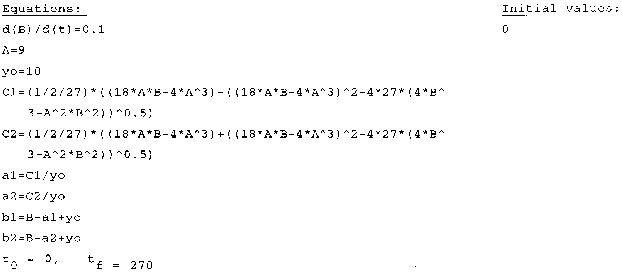
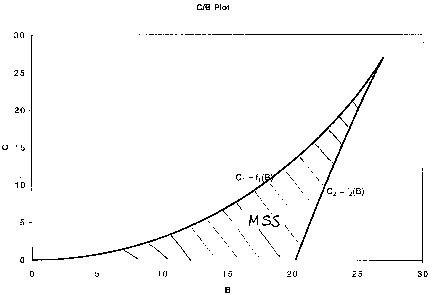
Table 1
|
Coordinate Transformation
C = ayo B = a + b – yo Now
|

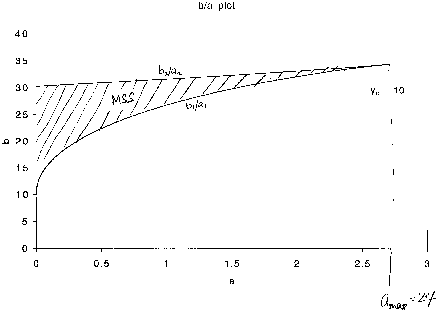
Part g)
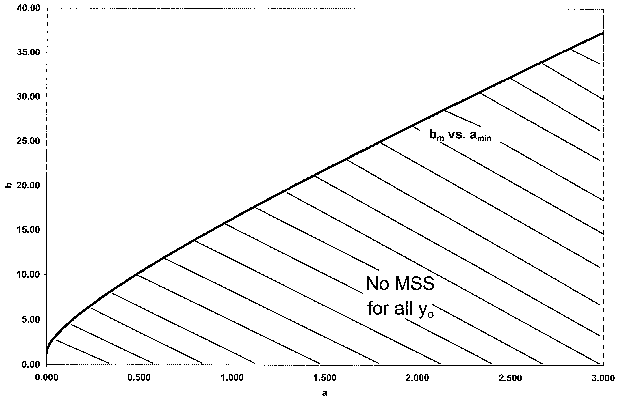
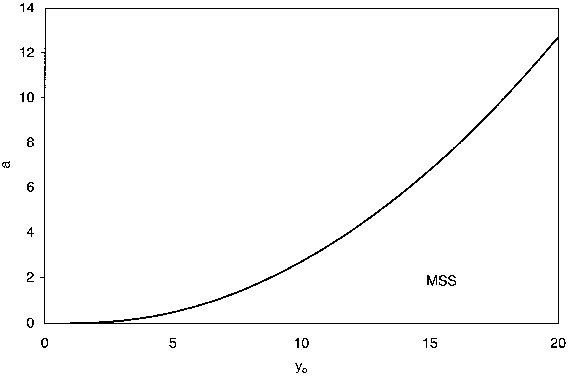
Develop a plot of a versus yo that divides the region into no MSS and MSS. Repeating the above procedure for various values of yo, we will see that amax increases as yo increases.
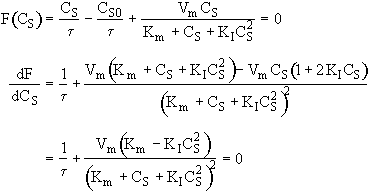
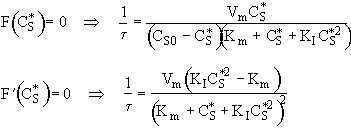
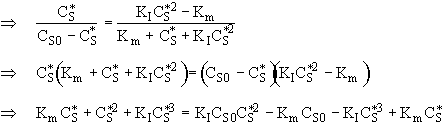
![]()
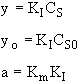
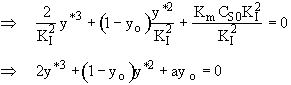
![]()
![]()
![]()
![]()
For only one real root for y*
![]()
![]()
![]()
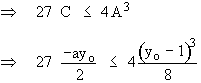
![]()
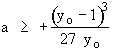
There will be no multiple steady states if 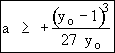
This is also mentioned in part (f) of the problem statement. 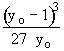 is the minimum value of
a above which there will always be only one steady state.
is the minimum value of
a above which there will always be only one steady state.
For yo
= 10 , amin = 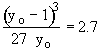
(see b/a plot)
Multiple steady states may occur if
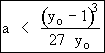
depending on the value of b (= t KI)
At bmin